Шевченко Н.Ю., Руднев М.Ю.

Прогнозирование производственной программы выпуска продукции с учетом предпрогнознаго анализа временных рядов

Донбасская государственная машиностроительная академия, Украина

Прогнозирование производственной программы выпуска продукции с учетом предпрогнознаго анализа временных рядов

Современная методология научного планирования деятельности предприятий включает: стратегическое планирование, составление прогнозов развития предприятий и внутрифирменное планирование.

Основными составляющими компонентами непосредственно системы внутрифирменного планирования являются система бизнес-планирования и система оперативно-производственного планирования. Успешное формирование нового бизнеса и планирование дальнейшего развития уже функционирующего предприятия не могут обойтись без четкого и научно обоснованного бизнес-плана. Входящая в состав бизнес-плана производственная программа предприятия является стержневым разделом плана любого уровня, так как определяет объем продукции.

Следовательно, прогнозирование объемов производства продукции даст возможность руководству предприятия эффективно организовать производственно-хозяйственную деятельность и тем самым обеспечить достаточный уровень прибыльности.

Предлагаемая в данной работе многоэтапная прогнозная модель предполагает наличие у лица, принимающего решения (ЛПР) фактических данных о предшествующих уровнях объемов производства продукции, которые могут быть использованы для построения с определенной точностью точечного и интервального прогнозов с использованием различных моделей.

Прогнозирование выполняется в следующие три этапа:

) прогнозирование некоторого необходимого и определенного на предыдущем этапе максимально возможного периода упреждения;

) построение доверительного интервала.

Для предпрогнозного анализа целесообразно использовать статистику Херста – «нормированный размах», позволяющую установить факт присутствия тренда во временном ряде. Так называемый H-показатель Херста (1) принимая значения , говорит о случайности временного ряда (события случайны и не коррелированны); если , то рассматриваемый временной ряд является персистентным или трендоустойчивым и характеризуется наличием долгосрочной памяти (события тем более коррелированны, чем ближе значение H-показателя к единице). Значения  указывают на антиперсистентность временного ряда и его зашумленность [1-2].

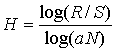, (1)

где  – среднеквадратическое отклонение ряда наблюдений ;

 – размах накопленного отклонения;

 – заданная константа, положительное число (автор показателя Херст эмпирически рассчитал эту константу для сравнительно краткосрочных временных рядов природных явлений как 0,5).

Для предпрогнозного анализа временного ряда целесообразно применить модификацию метода нормированного размаха Херста – новый алгоритм фрактального анализа, который получил название «алгоритм последовательного R/S-анализа». Преимущество данного алгоритма состоит в его способности выявления циклов (квазициклов) в рассмотренном временном ряде, а также вычисления нижней оценки глубины памяти (о начале этого временного ряда) [1].

Суть алгоритма последовательного R/S-анализа состоит в последовательном наращивании Н-траектории и R/S-траектории данного временного ряда. Данный метод оценить глубину памяти временного ряда: определяется точка, в которой R/S-траектория демонстрирует исчерпание в данном временном ряде начального цикла. В этой точке происходит изменение тренда («срыв с тренда») R/S-траектории без возвращения к первоначальному тренду каких-нибудь следующих точек. Начиная с этой же точки Н-траектория получает отрицательные приросты.

При этом необходимо учитывать, что после истечения цикла (квазицикла) теряется память о начальных условиях для рассмотренного временного ряда [1], то есть теряется долгосрочная коррелированность следующих наблюдений относительно начального. Таким образом, как нижняя оценка глубины памяти для рассмотренного временного ряда принимается длина первого цикла (квазицикла), что определяется длиной начального отрезка, концами которого является точка начала ряда и полученная точка (срыва с тренда).

После проведения анализа временных рядов объемов производства предшествующих периодов, скорректированных данными о фактических объемах продаж, может быть проведен прогноз на будущие периоды с целью оценки оптимальной производственной программы.

В разрабатываемой модели предполагается использование как точечную оценку прогноза при помощи линий тренда на основе нескольких регрессионных моделей для оценки ЛПР общего характера тенденций развития производства, так и интервальный прогноз с учетом сезонного характера производства на предприятии.

Для точечной оценки прогноза целесообразно использовать следующие модели регрессии:

) линейная;

) степенная;

) экспоненциальная;

) гиперболическая.

Кроме того, прогноз предполагает проведение процедуры верификации – проверки уровня достоверности, подлинности полученного варианта прогноза. В случае количественных методов прогноза это проверка адекватности прогностической модели и построение доверительного интервала.

Экстраполяция дает точечную оценку прогноза. Но точное совпадение фактических и прогнозных значений является маловероятным. Причины погрешности:

) субъективность выбора формы кривой;

) параметры кривой оцениваются на основе ограниченного числа наблюдений, каждое из которых содержит случайную компоненту;

) тренд характеризует средний уровень ряда в любой момент времени, следовательно, отклонения от тренда, которые наблюдались в прошлом, по-видимому, будут иметь место и в будущем.

Погрешность, связанная со вторым и третьим ее источником, может быть отражена в виде доверительного интервала прогноза. С помощью такого интервала точечный экстраполяционный прогноз преобразуется в интервальный (рис. 1).

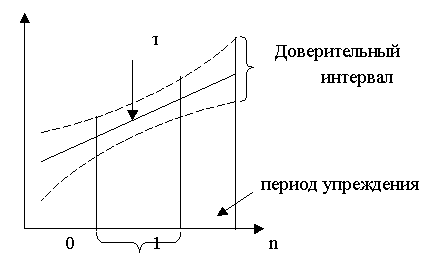
Рисунок 1 – Доверительный интервал тренда и прогноза в общем виде

Для оценки качества модели был необходимо использовать коэффициент детерминации, который позволит выбрать наиболее адекватную прогнозную модель.

Однако на практике приведенные выше прогнозные модели зачастую не дают качественный прогноз. Таким образом, необходимо также дополнить модель таким методом как метод Хольта-Уинтерса. Метод может учитывать как общий тренд, так и сезонность, что немаловажно, так как спрос, а соответственно и производство многих видов продукции имеет сезонный характер.

Модель Хольта-Уинтерса является расширением метода Хольта до трехпараметрического экспоненциального сглаживания. Это значит, что метод характеризуется тремя параметрами, которые должны быть эффективно подобраны для получения наиболее точного прогноза. Модели Хольта-Уинтерса могут учитывать сезонность в мультипликативном и аддитивном вариантах.

Мультипликативная модель прогнозирования Хольта-Уинтерса примет вид:

где  – параметр прогноза, очищенный от влияния тренда и сезонности (формула 3);

h – номер периода, на который строится прогноз;

 – параметр тренда (формула 4);

t – индекс текущего наблюдения;

St – сезонный профиль (формула 5);

p – период сезонности.

Соответствующие коэффициенты определяются по формулам:

где α – общий коэффициент сглаживания;

β – коэффициент сглаживания тренда;

γ – сезонный коэффициент сглаживания.

Как видно из модели, в ней учитываются значения предыдущих периодов, в том числе несуществующие. Поэтому для начала использования данной модели, ее необходимо инициализировать с начальным набором параметров. Так, предположив линейный характер тенденции временного ряда, найдем параметры a0 и b0.

Начальные значения параметра S определяются по формуле:

где  – фактическое и рассчетное значения показателей в ряду динамики;

p – период сезонности.

Коэффициенты сглаживания α, β, γ должны быть подобраны либо эмпирически на основе контрольной выборки либо путем методов оптимизации. Целесообразно использовать более универсальный второй способ.

Оптимизационная функция представляет собой стремящуюся к минимуму среднюю квадратическую ошибку модели:

где  – фактическое и рассчитанное по (2.29) значения показателей в ряду динамики;

n – общее число наблюдений;

α, β, γ – коэффициенты сглаживания.

Оптимизированы должны быть одновременно три переменные α, β и γ, а также зависимая от них средняя квадратическая ошибка. Таким образом, необходимо применить метод оптимизации в четырехмерном пространстве, например, с помощью метода покоординатного спуска Гаусса-Зейделя.

Метод покоординатного спуска сводит задачу о нахождении наименьшего значения функции многих переменных к многократному решению одномерных задач оптимизации по каждому проектному параметру.

Главное достоинство метода покоординатного спуска – возможность использования простых алгоритмов одномерной оптимизации [3].

Таким образом, найденные оптимальные коэффициенты α, β и γ позволят построить наиболее точный интервальный прогноз с учетом, как тренда, так и сезонного фактора.

Как и в случае с точечными прогнозами на основе трендов, необходимо оценить адекватность генерируемых моделью Хольта-Уинтерса значений. Должны быть оценены точность модели, а также проведен анализ автокорреляции случайных отклонений для исключения неадекватных данных.

Точность получаемых значений может быть оценена с помощью показателя относительной погрешности:

где Et – отклонение расчетного значения модели от фактического;

yt, Ft – фактическое и расчетное значения временного ряда.

Если данный показатель принимает значения меньше 5%, условие точности выполняется, модель отображает функционал, иначе, чем выше , тем ненадежней данные.

Оценить наличие автокорреляции в ряду случайных отклонений позволяет критерий Дарбина-Уотсона:

где Et – отклонение расчетного значения модели от фактического;

 – коэффициент автокорреляции первого порядка.

Таким образом, в результате оценки временных рядов объемов производства и проведения прогноза их значений на полученный в результате анализа период упреждения, ЛПР при помощи предложенного прогнозного инструментария может принять решение об объемах производства продукции на будущие периоды. Данные значения могут стать основой формирования производственной стратегии развития любого промышленного предприятия.

Список литературы

1. Максишко Н. К. О двух подходах к R/S-анализу временных рядов / Н. К. Максишко, В. А. Перепелица // Вісник Східноукраїнського університету ім. Володимира Даля. – 2005. – № 5(87). – С. 134-140.

2. Максишко Н. К. Про застосування алгоритму послідовного R/S-аналізу для одер-жання нечіткої оцінки глибини пам'яті часового ряду / Н. К. Максишко // Вісник Львівського університету. – 2006. – С. 516-521.

3. Васильев Ф.П. Методы оптимизации: В 2-х кн. Кн. 1: Учебник. – МЦНМО, 2011 г. – 620 с.
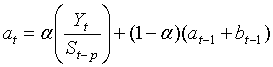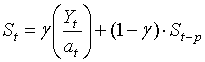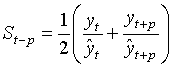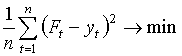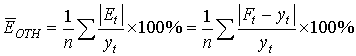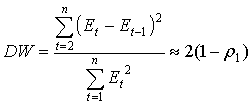