Серая О.В., Дунаевская О.И.
Нечеткая нелинейная транспортная задача
Нечеткая нелинейная транспортная задача
-->Традиционные задачи транспортной логистики формулируются в терминах линейного программирования. При этом используется предположение, что стоимость перевозки продукта по любому маршруту пропорциональна его объему. На практике часто такое предположение не выполняется. Целевая функция задачи при этом становится нелинейной. Задача усложняется, если при постановке задачи необходимо учитывать, что стоимость перевозки зависит не только от пары «поставщик-потребитель», но также от типа перевозимого груза, типа используемых транспортных средств и т.д. Возникающие при этом задачи становятся многоиндексными.
Общая формулировка ![]() -индексной нелинейной транспортной задачи такова: найти набор
-индексной нелинейной транспортной задачи такова: найти набор ![]() , минимизирующий целевую функцию
, минимизирующий целевую функцию
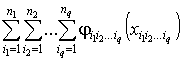 (1)
(1)
и удовлетворяющий ограничениям
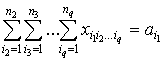 ,
, ![]() , (2)
, (2)
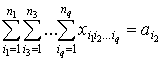 ,
, ![]() , (3)
, (3)
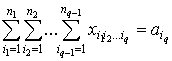 ,
, ![]() , (4)
, (4)
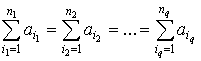 , (5)
, (5)
![]() ,
, ![]() ,
, ![]() .
.
В [1] предложена методика решения такой задачи, которая основана на следующей теореме.
Теорема.
Для того, чтобы набор ![]() был решением задачи (1)-(5) необходимо и достаточно, чтобы этот набор, удовлетворяя (2)-(5), минимизировал
был решением задачи (1)-(5) необходимо и достаточно, чтобы этот набор, удовлетворяя (2)-(5), минимизировал
т.е.
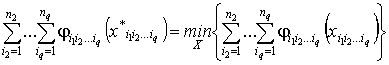 , для всех
, для всех ![]() . (6)
. (6)
Использование этой теоремы обеспечивает декомпозицию исходной задачи.
При этом, в частности, двухиндексная задача: найти набор ![]() , минимизирующий
, минимизирующий
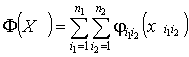 (7)
(7)
и удовлетворяющий ограничениям
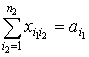 ,
, ![]() , (8)
, (8)
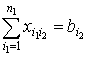 ,
, ![]() , (9)
, (9)
![]() ,
, ![]() ,
, ![]() , (10)
, (10)
сводится к решению ![]() одноиндексных задач вида:
одноиндексных задач вида:
найти набор ![]() , минимизирующий
, минимизирующий
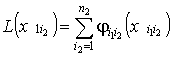 (11)
(11)
и удовлетворяющий ограничениям
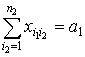 ,
, ![]() ,
,![]() ,
, ![]() . (12)
. (12)
Если при этом функции ![]() выпуклы вверх, то каждая из этих задач легко решается [2]. Естественные трудности возникают, если какие-либо параметры этих целевых функций – нечеткие величины. Возможный подход к решению таких задач состоит в следующем. Пусть целевая функция каждой из одноиндексных задач имеет вид
выпуклы вверх, то каждая из этих задач легко решается [2]. Естественные трудности возникают, если какие-либо параметры этих целевых функций – нечеткие величины. Возможный подход к решению таких задач состоит в следующем. Пусть целевая функция каждой из одноиндексных задач имеет вид
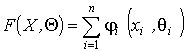 , (13)
, (13)
![]() - нечеткий параметр,
- нечеткий параметр, ![]() .
.
С использованием функций принадлежности ![]() нечетких параметров
нечетких параметров ![]() формируем функции принадлежности нечетких значений слагаемых целевой функции
формируем функции принадлежности нечетких значений слагаемых целевой функции ![]() , зависящие от
, зависящие от ![]() . Теперь положим значения нечетких параметров
. Теперь положим значения нечетких параметров ![]() равными их модальным значениям
равными их модальным значениям ![]() ,
, ![]() , и решим задачу отыскания набора
, и решим задачу отыскания набора ![]() , минимизирующего
, минимизирующего
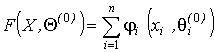 , (14)
, (14)
и удовлетворяющего ограничению
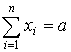 . (15)
. (15)
Пусть ![]() - решение этой задачи. Тогда в качестве решения задачи (13), (15) примем набор
- решение этой задачи. Тогда в качестве решения задачи (13), (15) примем набор ![]() , минимизирующий составной критерий
, минимизирующий составной критерий
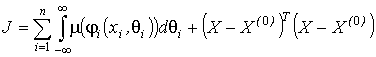 .
.
Смысл введенного критерия понятен. Первое слагаемое определяет суммарную площадь функций принадлежности слагаемых целевой функции задачи, зависящую от ![]() и которую желательно минимизировать, а второе – характеризует отклонение искомого решения от модального.
и которую желательно минимизировать, а второе – характеризует отклонение искомого решения от модального.
Рассмотрена методика решения многоиндексных нелинейных транспортных задач с планарными и аксиальными ограничениями. Сфотмулированы и доказаны теоремы, на которых базируются технологии получения решения. Описаны соответствующие вычислительные процедуры.
Литература.
1. Серая О.В. Многоиндексные нелинейные транспортные задачи / О.В. Серая, О.И. Дунаевская // Інформаційно-керуючі системи на залізничному транспорті. – Харків: ІКСЗТ, 2009. - № 5. – С. 25 – 30
2. Раскин Л.Г. Анализ сложных систем и элементы теории оптимального управления. –М.: Сов. Радио, 1976.-344с.
