Богомолов А.И., Катаргин Н.В., Костюнин В.И.

Математическая модель для оптимизации управления инвестициями региона

Развитие региона предполагает эффективное распределение средств между различными проектами при наличии бюджетных ограничений.  При оценке вклада проекта в общее благо региона мы будем учитывать его полезность (в относительных единицах, через функцию полезности), определяемую экспертным путём. Полезность мы будем считать основным показателем в рейтинговой оценке проекта. Мы выдвигаем гипотезу, что полезность проекта для региона монотонно возрастает с увеличением затрачиваемых на него средств, но предельная полезность, то есть приращение полезности на каждый следующий рубль, убывает при превышении некоторой величины. Это соответствует таким функциям как логистическая или логарифм.  В некоторых случаях можно использовать полином с ограниченной областью определения. Но, самое главное, проект важен не сам по себе, а важно его воздействие на социально значимые параметры региона: уровни образования, заболеваемости, смертности, рождаемости, преступности, социальной напряжённости и т.д.

Общая схема оптимального распределения средств при наличии бюджетного ограничения приведена на Рисунке 1.

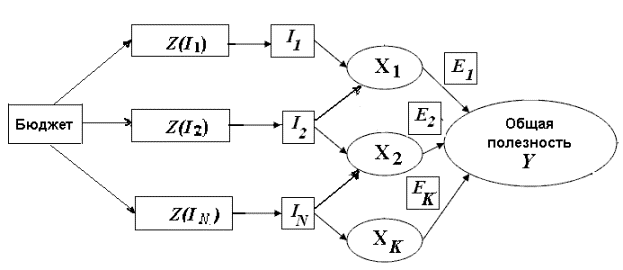
Рис.  1. Общая схема оптимального распределения средств.

Здесь: I_i –  i-й проект (внедрение новых технологий, модернизация транспортной системы, улучшение экологии и др.),Z(I_i) – затраты на  i-й проект, i= 1, …, N; Х_k – статистический показатель или экспертная оценка социально значимого параметра региона (уровни образования, заболеваемости, смертности, рождаемости, преступности, социальной напряжённости и т.д., преобразованные, чтобы с ростом показателя увеличивался Y);  E_k– эксперты k-й группы; k= 1, …, K.

Построение функции полезности отдельного проекта и его влияние на показатели региона реализуется экспертными методами. Общую полезностьY, полученную в результате  бюджетных затрат, можно оценить как сумму показателей:

             Y= SХ_k           i=1, 2, …, K.                             (1)

Можно предложить социально-экономико-математическую модель, аналогичную модели Стоуна для формирования потребительской корзины:

             Х_k  = f_k(Z₁, Z₂, …,Z_N)           i=1, 2, …, K.              

            Z₁+ Z₂+ …+Z_N= бюджет                                         (3)

где   Y– результирующий показатель, характеризующий качество жизни в регионе; 

Х_k– статистические показатели: уровни образования, заболеваемости, смертности, рождаемости, преступности, социальной напряжённости и т.д., преобразованные, чтобы с ростом показателя увеличивался Y;

Х_mink  – критические значения показателей;

 a_k– значимости показателей (эластичности), устанавливаемые экспертами;

 f_k(Z₁, Z₂, …,Z_N) – функции, описывающие влияние затрат на статистические показатели, построенные на основе экспертных оценок и экономико-математического моделирования. Мы используем логистическую функцию, предполагая, что каждый проект влияет только на один показатель, то есть i=k:

         Выражения (1) и (2) представляют собой целевые функции, которые надо максимизировать. Выражение (3) представляет собой бюджетное ограничение.

Таким образом, нахождение оптимального распределения ресурсов на реализацию отдельных проектов мы свели к решению задачи математического программирования. Модель позволит оптимизировать затраты по разным статьям с точки зрения достижения максимального результата Yпри ограниченности бюджета.

Рассмотрим условный пример оптимального распределения бюджета региона между  проектами трёх видов. Объём финансирования по соответствующим инновациям может меняться от 1 до 7 млрд. руб., т.е. бюджет составляет 7 млрд. руб.

Бюджетное ограничение записывается в виде:

                               Z(I₁) + Z(I₂) + Z(I₃)         = 7                                         (3)

Логистические функции полезности (линии), построенные по экспертным данным (чёрные фигуры), представлены на Рисунке 2. По оси абсцисс отложены ресурсы (деньги), необходимые для проекта,  по оси ординат – его полезность.

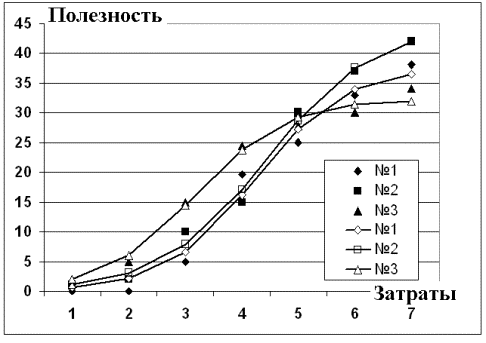
Рис. 2. Исходные данные и функции полезности проектов

Аналитические выражения получены методом наименьших квадратов с помощью функции Поиск решения MS Excel. Подставляя эти функции в выражения (1) и (2) и максимизируя Yпри бюджетном ограничении (3), мы использовали Поиск решения для получения искомых значений Z(I_i).

В результате были получены следующие значения:

для аддитивной модели (1):    Z(I₁) = 0;  Z(I₂) = 1,19;  Z(I₃)  =  5,81;                   

для мультипликативной модели (2):  Z(I₁) = 3,13;  Z(I₂) = 1,81;  Z(I₃)  =  2,05.

Методика может быть усовершенствована на основе оценки рисков  принимаемых решений по реализации проектов. Риск потерь по отдельному проекту вычисляется как произведение баллов на затраты, а суммарный риск  как корень из дисперсии суммы этих (независимых) величин:

Максимизируется величина Y/Риск.

Например, эксперты оценили в баллах риски проектов:  R₁= 4;  R₂= 8; R₃= 3. Результаты расчётов:

для аддитивной модели (1): Z(I₁) = 1,9;  Z(I₂) = 0,23;  Z(I₃)  =  4,88;                   

для мультипликативной модели (2): Z(I₁) = 3,29;  Z(I₂) = 1,18;  Z(I₃)  =  2,52.

Развитие данной методики на основе теории полезности может привести к весьма интересным и полезным результатам, как в научном плане, так и в практическом плане повышения качества планирования развития региона.