Белякова Т. Б.

Применение математического моделирования в целях минимизации прибыли торговых организаций

Проникновение математических методов в экономическую науку во многом обусловлено самой природой экономических процессов, да и спецификой самой науки. Познание количественных отношений экономических процессов и явлений опирается на экономические измерения. Точность измерений в значительной степени предопределяет и точность конечных результатов количественного анализа посредством моделирования. Поэтому необходимым условием эффектного использования математического моделирования является совершенствование экономических измерителей. Сформулированная экономическая задача в области максимизации прибыли торгового предприятия может быть также решена одним из разработанных математических методов. Следует отметить, что методы оптимального программирования эффективно используются для составления планов товарооборота и его структуры, рационов меню в общественном питании, для решения различных транспортных задач. Модели, построенные с использованием теории игр, применяются для решения альтернативных задач (размещения оборудования при наличии ограниченных площадей, организация продажи новых товаров и т.д.). Системы массового обслуживания используются при обслуживании большого количества покупателей, для расчета технологических процессов движения товаров. Методы сетевого планирования и управления дают хорошие результаты при построении моделей больших торговых центров, создании и освоении автоматизированных систем управления в торговле. Данный перечень не охватывает всех примеров применения математических методов в экономике, но он показывает необходимость проведения анализа при использовании математического аппарата в каждом конкретном случае.

Таким образом, математическое моделирование экономических явлений и процессов является важным инструментом экономического анализа, которое дает возможность получить всесторонне представление об исследуемом объекте, охарактеризовать и количественно проанализировать его внутреннюю структуру и внешние связи.

Допустим, что организация розничной торговли (магазин) имеет потенциальное количество поставщиков (оптовые базы, производители), являющихся основными поставщиками товаров с последующей их реализацией. При заключении договоров на поставку товаров, организация самостоятельно выбирает необходимый ассортимент продовольственных товаров и потенциальных поставщиков. Определим основные факторы, влияющие на данный выбор, это скидки покупателям, предоставляемые поставщиками, в зависимости от объема товара (чем больше объем закупаемого товара, тем больше скидки); качество предлагаемого товара и его производитель; условия транспортировки (поставщик может «брать на себя» транспортные услуги и включать их в покупную стоимость товара) и т. д.

Предприятия торговли, преследуя цель максимизации прибыли, могут отказаться от какого-либо поставщика либо от какого-либо товара, в случае если поставщик или товар не отвечает предъявляемым требованиям.

При этом величина оптимального объема закупаемого товара, при котором удастся достичь желаемого товарооборота, а, следовательно, и желаемой прибыли, на это момент будет неизвестна. Кроме того, данная величина будет ограничена денежными ресурсами, имеющимися на определенный момент у торговой организации, а также площадью торгового зала и складских помещений.

При построении математической модели, задачей которой является максимизации прибыли торговой организации при имеющихся ограничениях, все затраты, осуществляемые торговой организации были разделены на две группы: внешние и внутренние. К первой группе были отнесены расходы по доставке товаров от поставщиков до склада магазина, включая покупную стоимость этих товаров. Данные расходы во многом зависят от количества закупаемого товара и от конкретного поставщика.

Внутренними признаются расходы, полностью связанные с реализацией товаров, включая расходы на оплату труда торгового персонала, отчисления на социальные нужды, амортизацию торгового оборудования, расходы по хранению, фасовке товаров, рекламные расходы и т.д. Данный вид расходов может быть определен по данным бухгалтерского учета по различным группам товаров с использованием учетно-распределительного метода.

Стоит задача определить такой уровень торговой надбавки на товар, а, следовательно, и возможность определить розничную цену на каждый вид товара, чтобы предприятие торговли смогло возместить покупную стоимость товара, расходы на доставку товара, издержки обращения и получить максимальный уровень прибыли.

Для построения математической модели были введены следующие обозначения:

q – количество видов товара одного ассортимента, получаемые от поставщиков,Q = {1, …, q};

- множество поставщиков, у которых организация может получать k-й товар, k є Q;

, - верхняя и нижняя граница продажной цены k-того товара для i-того поставщика, i є, k є Q;

- имеющийся объем средств у организации для приобретения товара;

Введем переменные задачи:

- - объем k-го товара, получаемого от i-го поставщика,

- продажная цена k-го товара, полученного от i-го поставщика,

i є , k є Q, y = ();

Кроме того, считаем известными следующие функции:

- верхняя граница для объема поставок k-ого товара от i-го поставщика при продажной цене ;

S(x) – издержки обращения, рассчитанные по группам товара с помощью учетно-распределительного метода;

- покупная цена получаемого k-го товара от i-го поставщика в объеме .

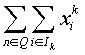=-общий объем, приобретенного товара;

- площадь торгового зала, требуемая для реализации товара в объеме ;

-площадь складских помещений, требуемых для хранения товара в объеме ;

-имеющаяся площадь торгового зала;

- имеющаяся площадь складских помещений.

Таким образом, с учетом имеющихся данных и ограничений можем построить следующую математическую модель для решения задачи максимизации полученной прибыли торгового предприятия:

- целевая функция задачи состоит в максимизации прибыли организации (1)

при ограничениях:

- ограничение на объем средств, который может использовать организация для приобретения товаров (2)

- ограничения на объем товаров, получаемых от поставщиков (3)

, , - ограничения на величину розничных цен, определяемых торговой организацией (4)

-ограничение на площадь торгового зала (5)

- ограничение на площадь складских помещений (6)

Данная задача относится к области нелинейного программирования, поэтому для ее решения могут быть использованы различные математические методы, которые в дальнейшем должны быть использованы для составления компьютерной программы, позволяющей решить ряд теоретических и прикладных задач в области торговли.

Литература:

1) Математические модели в экономике: Иванилов Ю. П., - М., "Наука", Главная редакция физико-математической литературы, 1979, 304 стр.2005.

2) Мажукин В.И., Королева О.Н. Математическое моделирование в экономике: Учебное пособие/ В.И. Мажукин.- М. Флинта: Московский гуманитарный университет,2004-4 232 с. 56 с: ил.

3) http://student6.ru/MODELIR.html