Галкина Е.В.

Статистический вывод в финансовом контроле и менеджменте

Наиболее востребованными в аудиторской и иной контрольной деятельности в сфере экономики являются методы оценки разностей (различий), которая применяется к суммовым показателям, и оценки доли нарушений, которая применяется к бинарным значениям (типа «да/нет»).

1. Определяется объем выборки. Профессор Ю.Ю. Кочинев отмечает, что на основе преобразования формулы Пуассона объем выборки определяется по формуле (1) [2, с. 137]:

n=1/p*2,3*(-lgR)                                                                                              (1)

В формуле (1) приняты следующие условные обозначения:

n – объем выборки;

p – отношение ожидаемой ошибки генеральной совокупности (M) к объему генеральной совокупности (N);

R – риск (единица минус уровень надежности (P), выраженный в долях единицы).

«Величину G=2,3*(-lgR)  в литературе называют коэффициентом надежности» [2, с. 137]. Его значения приводятся профессором Ю.Ю. Кочиневым – таблица 1 [2, с. 137].

Таблица 1 – Значения коэффициента надежности

В качестве ожидаемой ошибки генеральной совокупности используется допустимая ошибка (S). Уровень существенности (s) будет равен S/N. Тогда оптимальный объем выборки определяется по формуле (2) [2, с. 137]:

n=N/S*G=G/s                                                                                                   (2)

Например, если уровень существенности установлен аудитором в размере 0,01 (один процент), а уровень надежности в размере 0,95 (девяносто пять процентов), то объем выборки равен:

n=3,0/0,01=300 (единиц совокупности).

После определения объема выборки осуществляется проверка документов, попавших в выборку.

2. Вычисляются разности (абсолютные) между правильными и фактическими учетными величинами, D_i.

3. Рассчитывается выборочная разность (как средняя арифметическая всех разностей, включая нулевые разности), .

4. Вычисляется стандартное отклонение разностей, S_D– формула (3):

S_D= ,                                                                                           (3)

где n – количество элементов в выборочной совокупности.

5. Определяются границы доверительного интервала, содержащего сумму разностей элементов генеральной совокупности – формула (4):

N±N(t_n-1),                                                                                    (4)

где N – количество элементов генеральной совокупности;

t_n-1– критическое значение t-статистики с количеством степеней свободы, равным n-1, соответствующее площади фигуры, ограниченной правым хвостом распределения Стьюдента.

Так, если из генеральной совокупности, составляющей 500 документов, сделана выборка в 100 документов, из которых в 12 документах выявлены следующие количественные искажения,D_i, (в условных денежных единицах): 28; -2,5; 35,6; 4,59; -8,46; 34,9; 7,89; 52,3; -15,42; 16,34; 12,52; 12,01, – то оценка разности будет определена следующим образом.

 = (28-2,5+35,6+4,59-8,46+34,9+7,89+52,3-15,42+16,34+12,52+12,01)/100=1,7777.

S_D= =8,19925.

Полная разность находится в интервале

от 500*1,7777-500*1,9842*8,19925/*=160,545

до 500*1,7777+500*1,9842*8,19925/*=1617,155.

Критическое значение t-статистики для доверительной вероятности 95% (1,9842) получено по таблице Д.3 [1, с. 1242-1245]. Для выбранной аудитором доверительной вероятности площадь фигуры равна разности единицы и доверительной вероятности (в долях единицы), деленной на два (так как оценка интервала двухсторонняя). Расчеты произведены в редакторе MS Excel, результаты округлены и несколько отличаются от результатов расчетов, которые были бы выполнены вручную (за счет меньшей точности при многократных округлениях до малого числа знаков при промежуточных ручных расчетах). Рабочий лист расчетов показан на рисунке 1.

Рисунок 1. Рабочий лист определения разности

Алгоритм проведения расчетов в режиме проверки формул представлен на рисунке 2. Программа позволяет автоматически пересчитывать все итоговые значения при изменении переменных.

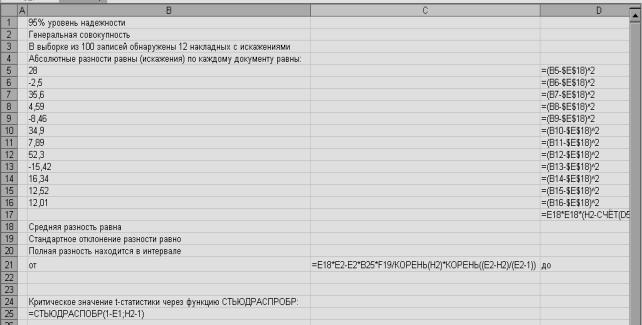
Рисунок 2. Рабочий лист определения разности (режим проверки формул)

Анализ ранговых (то есть выраженных в качественном, позволяющем упорядочить, но не точно сопоставлять значения (например, да/нет, больше/меньше), измерителе) отклонений.В контроле, в том числе финансовом контроле, необходимой является оценка доли нарушений (количества нарушений в общем количестве фактов). Односторонний доверительный интервал, содержащий долю признака в генеральной совокупности, определяется по формуле (5) [1, с. 487]:

Верхняя граница= p_s+ Z,                                                (5)

где p_s– доля признака в выборочной совокупности (например, количество неправильно оформленных документов к количеству проверенных документов);

Z – критическое значение стандартизованного нормального распределения, соответствующее интегральной вероятности, равной 1 - α.

Z определяется по статистическим таблицам или с помощью функции MS Excel НОРМСТОБР(вероятность).

Так, если аудитор при проверке 300 накладных из 8000 накладных на отпуск товара обнаружил, что в 26 накладных оформлялись без предварительного заказа, что в проверяемой организации считается нарушением требований внутреннего контроля. Тогда p_s= 26/300=0,0867 (с округлением). Z для доверительной вероятности 95% равно около 1,6449.

Верхняя граница = 0,0867+1,6449=0,1129.

Таким образом, односторонний доверительный интервал для доли накладных, при оформлении которых были нарушены требования внутреннего контроля,  равен около 11,29%.

Если в организации установлено предельно допустимое отклонение (предел), то фактический односторонний интервал сопоставляется с этим отклонением. Если фактическая оценка не более предела, то может быть сделан вывод о том, что требования контроля не нарушаются, и наоборот. Так, если предел для рассматриваемой организации установлен ее руководством на уровне 2%, то факт (11,29%) превышает предельное значение, и аудитор должен сделать вывод о существенности отклонений от внутренних правил.

В целом, статистические методы нашли широкое применение в разных видах контроля, в том числе как финансового, так и нефинансового, что нашло отражение на международном уровне и в системе государственных стандартов Российской Федерации. Такой контроль рассматривается как часть системы менеджмента. В частности, национальный стандарт Российской Федерации ГОСТ Р 51901.16-2005 «Менеджмент риска. Повышение надежности. Статистические критерии и методы оценки» (утвержденный и введенный в действие приказом Федерального агентства по техническому регулированию и метрологии от 30 сентября 2005 года № 235-ст), подготовлен на основе международного стандарта МЭК 61164:1995 «Повышение надежности. Статистические критерии и методы оценки» (IEC 61164:1995 «Reliability Growth – Statistical test and estimation methods») и технически модифицирован для обеспечения соответствия правовым и нормативно-правовым требованиям, установленным в Российской Федерации. Данный стандарт содержит термины и определения, обозначения, указания по использованию моделей для программ улучшения надежности, статистические методы оценки и проверки гипотез, примеры.

Менеджмент надежности ориентирован на достижение таких целей организации, как (п. 4.1 ГОСТ Р 51901.2-2005 «Менеджмент риска. Системы менеджмента надежности»):

- определение потребностей и ожиданий заказчика в области надежности  (продукции и т.п.) и методов их достижения;

- разработка планов надежности;

- измерение и повышение эффективности системы менеджмента надежности;

- облегчение взаимодействия в сфере надежности.

Статистика позволяет делать количественно обоснованные выводы в разных областях и для разных целей контроля и в целом управления.

Литература:

1. Левин, Д. Статистика для менеджеров с использованием  Microsoft Excel, 4-е изд./ Д.М. Левин, Д. Стефан, Т.С. Кребиль, М.Л. Беренсон: Пер. с англ. – М.: Издательский дом «Вильямс», 2004. – 1312 с. – ISBN 5-8459-0607-5.

2. Кочинев, Ю.Ю. Аудит: теория и практика/ Ю.Ю. Кочинев. 5-е изд. – СПб.: Питер, 2010. – 448 с.: ил. – (Серия «Бухгалтеру и аудитору»). – ISBN 978-5-49807-579-2.