Южанников А.Ю., Южанникова М.А.

Ранговый анализ экономических ценозов

Целью данной работы является анализ графика развития экономических ценозов, а также его сравнение с «идеальной кривой». Построение идеальной линии состояния  ценозов может послужить стандартом при сравнении и дальнейшем развитии той или иной системы.

Научно-техничекий прогресс достиг такой ступени развития, когда видовое разнообразие выпускаемых изделий соизмеримо с видовым разнообразием в природе. Законы формирования технических и экономических систем, состоящих из отдельных элементов схожи с законами формирования биосистем из отдельных особей [2].

По мнению Б. И. Кудрина, законы развития и поведения биологических и искусственных систем имеют общность, поэтому представляется возможным и необходимым описать законы функционирования и развития сложных экономических систем, основываясь на ценологическом подходе к их изучению.

Решение этих проблем опирается на объективные законы, отражающие закономерности развития природы. В системе понятий «объект – состояние – связи – теория» представление об объекте, его состояниях и законах выступают основой для представлений о физическом мире, а также служат базой для выработки экономических и физических теорий и соответствующей картины мира. Любое изделие имеет свое функциональное предназначение (в этом его сущность, содержание), которое реализуется с помощью определенного конструктивного решения (это явление, форма) [3].

Техноценоз определён как сообщество технических изделий. Исследование любого техноценоза начинается с выделения его отдельно составляющих элементов (особей) в пространстве и во времени. Затем особи распределяют в зависимости от вида (соотношение модели, марки, размера). Следующее, что существенно, выделяют из определённого техноценоза часть изделий – семейство изделий.

Экономический ценоз также определен как самоорганизующееся многовидовое сообщество организаций (особей) различных отраслей (популяций) выделенного территориально-административного образования, характеризующееся связями различной силы (сильными, средними и преимущественно сла­быми), объединенное совместным использованием природных (экоценозы), технетических (техноценозы), социальных (социоценозы) ресурсов и экономических ниш спроса на продукцию, товары и услуги, с действием внутривидового и межвидового отбора [4].

Свойства техноценозов как системы заключаются в следующем:

1) любой ценоз индивидуален, два изделия одного вида неразличимы в пределах паспортных характеристик;

3) для техноценоза принципиально не может существовать документация, подобная паспорту на изделие, которая полностью описывает его;

4) время жизни техноценоза бесконечно велико относительно времени выпуска изделия как вида и времени его эксплуатации как отдельной особи;

5) изделие создается на основе классических законов физики и химии, разброс параметров подчиняется, в частности, нормальному закону;

6) построение техноценоза определяется законами техноэволюции, а структура образующих его изделий по повторяемости видов устойчива и определяется параметрами гиперболического Н-распределния, у которого отсутствует математическое ожидание, а дисперсия теоретически бесконечна;

7) техноценоз не имеет четких и очевидных границ: каждый специалист определяет их по-своему;

8) выбор изделия для техноценоза, его заказ, размещение, эксплуатация, замена во многом случайны, неформализуемы, тогда как само изделие и его составляющие рассчитываются по жестким, причинно обусловленным формулам [5].

Структура ценозов описывается разными типами распределений:

–  видовое распределение (зависимость числа видов от количества особей в виде);

– ранго-видовое (ранговое представление основывается на расположении элементов в порядке убывания величины описывающего их параметра или частоты появления)

– ранговое по параметру (при расположении видов а порядке уменьшения какого-либо параметра) [5].

Для моделирования невозрастающей функции всех трёх распределений применяются выражения (таб. 1):

Таблица 1

Математическое описание гиперболического Н-распределения

Теория ценозов объясняет механизм формирования гиперболических видового, ранго-видового и рангового по параметру распределений тем, что в биологии называют борьбой видов за существование (естественный отбор видов). Положения отбора распространяются на ценозы любой природы с введением, соответственно, понятий энергетического, информационного, документального, интеллектуального, социального и других отборов.

Борьба видов за существование – это борьба за ограниченный ресурс, предоставленный системе в целом. Под объёмом для ценоза следует понимать объём пространства в координатах внешних ресурсов, требуемых для функционирования особей-элементов. Размерность пространства объёма и физическая природа внешних ресурсов отличаются для разных систем-ценозов [6].

На этапе развития ценоза каждый вид стремится занять весь объём, предоставляемый системе, поэтому число особей всех видов растёт. Однако при достижении ограничений по ресурсу виды вступают в конкурентную борьбу за ресурс, и формируется структура, соответствующая видовому Н-распределению, число особей практически перестаёт изменяться. Число видов изменяется значительно медленнее, чем число особей для ценозов любой природы.

В основе методологического исследования ценоза лежит ранговый анализ. В статике распределение можно изобразить графически в виде гиперболы. Среди распределений рангового анализа особое место занимает видовое. Существует мнение, что оно является наиболее фундаментальным. Имеются теоретическое обоснование и эмперическое подтверждение тому, что, с одной стороны, видовое распределение есть взаимообратные формы одного распределения, а с другой – что бесконечная совокупность ранговых параметрических распределений техноценоза математически свертывается в одно видовое [5, 7].

Видовое распределение представляет собой зависимость числа видов с одинаковым числом особей от числа особей в виде, которым представлен ценоз. Графически это проиллюстрировано на рис.1:

Количество видов, имеющих

данную численность, ед

  Ω

400

         100

                                                                                                                             x       

   100                                       700        Возможная численность, шт

Рис.1. Видовое распределение

Видовое распределение устанавливает основополагающую взаимосвязь между массовостью элементов различных видов в ценозе и их разнообразием. Математически оно относится к гиперболическим безгранично делимым распределениям [5].

Ранго-видовое распределение также может быть изображено в графической форме (рис.2). В отличие от видового распределения, оно отражает зависимость количества особей, которым представлен вид в ценозе, от ранга R.

Количество особей, которым

представлен вид в ценозе, ед.

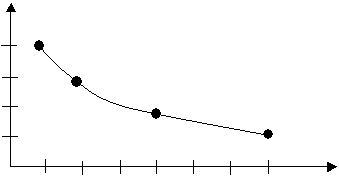   Λ

200

50

                                                                           R

               1                                          7     Видовой ранг     

Рис.2. Ранго-видовое распределение

В ходе рангового анализа также строятся графики ранговых  распределений по каждому из видообразующих параметров (рис.3). Однако здесь  прослеживается определенная специфика, заключающаяся в том, что в ранго-видовом распределении ранжируются виды, а в параметрическом – особи. Первый ранг r=1 присваивается особи с наибольшим значением параметра, далее – имеющей наибольшее значение параметра после первой.

Параметр 

  W

50

10                                                                                 r

             1                                            7          Параметрический ранг    

Рис.3. Ранговое распределение по параметру

Очевидно, что для всех трех типов распределения можно построить огромное количество гладких аппроксимирующих кривых, которые отражают функционирование особей-элементов в развитии того или иного ценоза. Для определения оптимального соотношения этих особей в данной работе предлагаем построить такую идеальную кривую, которая бы служила эталоном в развитии ценоза [3].

Как известно, идеальное соотношение отдельных составных частей какого-либо объекта базируется на пропорциональном делении, которое неразрывно связано с «Золотым сечением» и числами Фибоначчи.

«Золотое сечение» – это такое пропорциональное деление отрезка на две неравные части, при котором весь отрезок так относится к большей части, как большая к меньшей (c: b= b: a= 1,618). Такие отношения в рассматриваемой пропорции обозначаются буквой Ф в честь древнегреческого скульптора Фидия, в творчестве которого широко использовано этот уникальный метод. Гармоническое деление отрезка можно представить в следующем виде (рис.4):

                               a                                 b

                                                     c

Рис.4. Золотое сечение

Понятие «Золотое сечение» неразрывно связано с числами Фибоначчи.

В 1202 году итальянский купец и математик Леонардо Пизанский (больше известный как Фибоначчи), издал свое сочинение «Liber abacci», в котором он, решая задачу про кроликов, получил последовательность чисел, где каждый последующий член равен сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. Позднее эта последовательность чисел получила название ряда Фибоначчи [8].

В 1753 г., математик Роберт Симпсон заметил, что при увеличении порядкового номера члена ряда Фибоначчи отношение последующего члена к предыдущему приближается к числу, равному Ф = 1,618.

Также Ф = 1,618 является положительным корнем уравнения:

;                                               (1)

Для обобщенного варианта Золотых р-сечений, предложенного А.П. Стаховым и И.В. Витенько, выведена пропорция: [9]:

с : b= .                                             (2)

Тогда обобщенное уравнение для Золотых р-сечений выглядит следующим образом:

 .                                        (3)

Значения корней уравнения для Золотыхр-сечений при разных параметрах р  представлены ниже (таб.2) [9]:

Таблица 2

             Опираясь на представленные данные, подставим значение =1,618 при р=1 в формулу, которая описывает «идеальную кривую»:

                                                     (4)

             Для графика «идеальной кривой» построим ряд значений (таб.3):  

Таблица 3

Тогда график для данной функции будет выглядеть следующим образом (рис.4):

             y

1,618

    1,0

              0,2

                            1      2       3      4       5     6       7      Ранг, r

Рис.4. Идеальная кривая

Применительно к экономическим ценозам следует отметить следующее: математическая статистика, использующая процедуру усреднения (математическое ожидание), наиболее подходит для исследования предприятий одного вида. При исследовании ценозов, включающих большое количество видов, задача теряет свой первоначальный смысл.

Разнообразие видов и диапазон разброса параметров организаций-особей в экономических ценозах всегда настолько велик, что это делает невозможным применение привычной для нас классической математической статистики. Отсюда возникает потребность оперировать выборкой параметров в целом. Для этого необходимо построить ранговое распределение особей экономического ценоза [10].

Установлено, что в рыночной экономической среде под воз­действием внешней среды и совокупности внутренних факторов происходят следующие процессы. С одной стороны существует потребность в видах деятельности (услугах, продуктах, издели­ях), а с другой стороны действуют ограничения по производству этого вида деятельности (налоги, сырье, ресурсы, база, персо­нал). Это приводит к тому, что организации-особи одного вида деятельности на конкретной территории и в конкретных услови­ях нужны и доступны, потому и развиваются, их количество уве­личивается, а организации-особи других видов деятельности не востребованы и потеряли возможность существовать, потому их количество уменьшается [11].

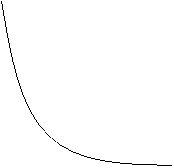
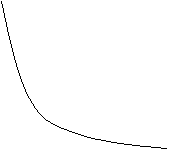
Со временем перемещение организаций-особей по видовому распределению происходит не сразу в многочисленные (или обратно) касты, а постепенно. Это перемещение представлено в разных вариациях и требуют индивидуального управленческого решения (рис.5, 6, 7):

1. Увеличение рангового коэффициента и изменение первой точки графика (увеличение разрыва между крупными и мелкими организациями-особями):

                                         β             

                                                                      r

Рис.5. Развитие ценоза при увеличении рангового коэффициента

β– идеальная кривая развития экономического ценоза;

 – первая точка графика растет. Чтобы достигнуть гармоничное развитие экономического ценоза, следует направить воздействия на укрупнение мелких особей-элементов;

 – первая точка графика не меняется. Чтобы достигнуть гармоничное развитие экономического ценоза, следует направить силы на рост мелких и средних особей-элементов;

 – первая точка графика уменьшается, то есть увеличение разрыва произошло из-за превалирования спада в развитии мелких элементов по сравнению с крупными. Чтобы достигнуть гармоничное развитие экономического ценоза, следует в первую очередь развивать мелкие особи.

2. Ранговый коэффициент не изменяется (экономический ценоз стабилен, соотношение между крупными и мелкими организациями-особями не меняется):

                                                                    r

Рис.6. Развитие стабильного ценоза

 – первая точка растет. Крупные и мелкие организациии-особи развиваются одновременно и пропорционально;

 – первая точка не изменяется. Этот случай характерен для многономенклатурных предприятий, работающих с номинальной загрузкой;

 – первая точка уменьшается. Спад в развитии наблюдается у всех элементов экономического ценоза в равной степени. Управленческие решения в данном случае должны быть направлены на всю систему в целом с целью прекращения спада. Этот случай характерен для предприятий, сокращающие объемы производства по всей номенклатуре.

3. Уменьшение рангового коэффициента и изменение первой точки графика (уменьшение разрыва между крупными и мелкими организациями-особями):

                                                                  β

                                                                        r

Рис.7. Развитие ценоза при уменьшении рангового коэффициента

  – первая точка графика растет, ценоз развивается в основном за счет более быстрого развития мелких организаций-особей. Чтобы достигнуть гармоничное развитие экономического ценоза, следует направить воздействия на ускорение развития крупных особей-элементов;

 – первая точка графика не меняется в силу того, что мелкие элементы развиваются, а крупные нет. Чтобы достигнуть гармоничное развитие экономического ценоза, следует направить силы на дальнейшее развитие крупных особей-элементов;

 – первая точка графика уменьшается, то есть увеличение разрыва произошло из-за превалирования спада в развитии крупных элементов по сравнению с мелкими. Чтобы достигнуть гармоничное развитие экономического ценоза, следует в первую очередь развивать крупные особи. Этот случай характерен для предприятий, сокращающих основное производство.

Данные процессы являются следствием действия естествен­но- информационного отбора, аналогичного естественному от­бору Ч. Дарвина, который, применительно к ценозам организа­ций, разделяется на внутривидовой и межвидовой отборы. Внут­ривидовой отбор происходит на основе конкуренции между ор­ганизациями-особями одного вида деятельности. Межвидовой отбор происходит на основе конкуренции между организациями-особями различных видов − по сути конкуренции между видами деятельности.

Следовательно, опираясь на объективную закономерность инфраструктуры экономических ценозов в мегаценозе, возможно управление конкуренцией, то есть осуществление антимонопольной политики и развитие предпринимательской среды в целом. На основе этого постулата логично создавать и корректировать механизмы воздействия на структуру рыночной экономической среды.

Литература:

1. Большой энциклопедический словарь /  И. Лапина [и др.]. М.: Астрель, 2008. – 1248 с.

2. Кудрин, Б.И. Античность. Символизм . Технетика / Б.И. Кудрин. – М.: Электрика, 1995. – 120 с.

3. Южанников А.Ю. Золотое сечение и техноценозы в системе электроснабжения: монография  / А.Ю. Южанников. – Красноярск: Поликор, 2009. – 288 с.

4. Фуфаев, В.В. Экономические ценозы организаций / В.В. Фуфаев.  − М.: Абакан: Центр системных исследований, 2006. − С. 3−38.

5. Кудрин, Б.И. Введение в технетику / Б.И. Кудрин. – 2-е изд. перераб. и доп. – Томск: Изд-во Томск.гос.ун-та, 1993. – 552 с.

6. Кузьминов, А. Н. Методология ценологического анализа транспортных систем в условия конкуренции. «Ценологические исследования» /   А.Н. Кузьминов. – М.: Технетика, 2011. – 400 с

7. Гнатюк, В.И. Закон оптимального построения техноценозов / В.И.Гнатюк. – Вып. 29. Ценологические исследования. – М.: Изд-во ТГУ – Центр системных исследований, 2005. – 384 с.

8. Воробьев, Н.Н. Числа Фибоначчи / Н.Н.Воробьев.  – М.: Изд-во "Наука", 1961. – 144 с.

9. Стахов, А.П. Код да Винчи и ряды Фибоначчи / А.П. Стахов, А.А. Слученкова, И.В. Щербаков. – СПб.: Питер, 2007. – 320 с.

10. Лозенко, В.К. Менеджеру – основы технознания и технетики // Бизнес-образование. – 2002. - №2. – С.53-62.

11.  Ламанский, М.Г. Оценка эффективности инвестиционной инфраструктуры предпринимательства.: дис. канд. эк. наук / М.Г. Ламанский. – Иркутск. – 200 с.