Таганов А.И., Гильман Д.В.

Задачи и методы нечеткой идентификации и нечеткого мониторинга процессных рисков проекта

Постановка задачи

,                                                                             (1)

где   - набор эталонных рисковых ситуаций проекта, соответствующих , которые хранятся в библиотеке контролируемых рисков;  - текущая рисковая ситуация проекта;  - отображение  в , характеризующее степень их соответствия;  - порог достоверности нечеткого соответствия эталонной и текущей ситуации проекта;  - структура предпочтений экспертов по рискам;  - набор алгоритмов, позволяющих определять соответствие текущей ситуации проекта   (с некоторым порогом достоверности нечеткого соответствия ) ситуациям из набора эталонных ситуаций .

Для решения первой задачи с областью определения (1) могут быть адаптированы и использованы методы и алгоритмы, представленные в [2, 5], которые основываются на использовании и построении расплывчатых ситуационных моделей принятия решений в условиях нечеткости.

Область решения второй задачи, связанной с определением оптимальной альтернативы реагирования на идентифицированное рисковое событие может, быть представлена кортежем:

,                                                                            (2)

где  - множество альтернатив реагирования на идентифицированное рисковое события ;  - отображение  на ;  - структура предпочтений экспертов по рискам;  -набор требуемых алгоритмов для решения задачи определения наиболее предпочтительной (рациональной) альтернативы реагирования  на идентифицированное рисковое событие  согласно .

Способы решения задачи

Первый способ  (алгоритм ) решения поставленной задачи, основывается на использовании опыта одного эксперта по рискам. Считается, что эксперт по рискам в терминах предпочтительности определяет матрицу предпочтительности альтернатив реагирования на идентифицированное рисковое событие . Далее в соответствии с предлагаемым способом для нечеткого отношения предпочтения  строится нечеткое отношение строгого предпочтения , определяемое функцией принадлежности:

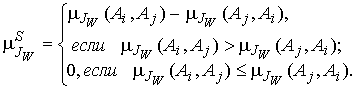                                          (3)

После этого вычисляется нечеткое подмножество недоминируемых альтернатив реагирования , ассоциированное с  и включающее те альтернативы, которые не доминируют ни над какими другими альтернативами реагирования, определяемыми функцией принадлежности:

.                                                             (4)

Для любой альтернативы реагирования  значение   понимается как степень недоминируемости этой альтернативы, то есть степень, с которой   не доминирует ни над одной из альтернатив реагирования множества ;  означает, что никакая альтернатива  не может быть лучше  со степенью доминирования ; иначе говоря, может доминировать над другими альтернативами, но со степенью не выше . Рациональным будем считать выбор альтернатив, имеющих по возможности большую степень  принадлежности множеству . И, следовательно, за оптимальную примем альтернативу , для которой значение  максимально:

.

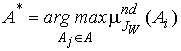Второй способ(алгоритм ) учитывает возможности привлечения группы менеджеров по рискам для задания предпочтительности альтернатив реагирования на идентифицированное рисковое событие и позволяет получить более объективное решение задачи с областью определения (2) [2, 6]. В этом варианте на множестве всевозможных альтернатив реагирования   каждый эксперт по рискам задает свое видение важности альтернатив реагирования в терминах предпочтительности . Главный менеджер (руководитель проекта) по-разному может относиться к мнению каждого эксперта по рискам, что может находить отражение в весовых коэффициентах , (где , ), соответствующих каждому из специалистов.

В этих условиях для определения оптимальной альтернативы реагирования на идентифицированное рисковое событие, в соответствии с предлагаемым вторым способом (алгоритмом ), необходимо для каждого отношения предпочтения  построить нечеткое отношение строгого предпочтения , функция принадлежности которого определяется по формуле (3). Далее построить свертку  отношений предпочтения, как пересечение нечетких отношений строгого предпочтения экспертов, по формуле:

= .                                                       (5)

Таким образом, получается новое нечеткое отношение нестрогого предпочтения. Далее на основе  можно построить отношение строгого предпочтения   с функцией принадлежности :

.

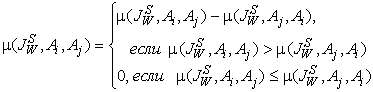Следующим шагом следует определить множество недоминируемых альтернатив   с функцией принадлежности:

.                                                         (6)

На следующем шаге необходимо построить выпуклую свертку  отношений , которая определяется как  с функцией принадлежности:

.                                                                   (7)

Для нечеткого отношения предпочтения  аналогично строится отношение строгого предпочтения  и множество недоминируемых альтернатив .  Из формул (5)-(7) можно сделать вывод, что множества   и  несут дополняющую друг друга информацию о недоминируемости альтернатив реагирования.

Далее рассматривается пересечение полученных множеств  и   с функцией принадлежности:

.

Рациональным считается выбор той альтернативы  из ,для которой значение  максимально:

, .

Третий способ(алгоритм ) решения задачи в постановке (2) характеризуется тем, что значимость мнений экспертов по рискам оценивается при помощи нечеткого отношения предпочтения , заданного на множестве экспертов  с функциями принадлежности ,  , значения которых обозначают  степень предпочтения мнения эксперта  по сравнению с мнением эксперта  [2, 6]. В данном случае для решения поставленной задачи необходимо аналогично второму способу для каждого  построить  и .

Далее для ясности введем обозначение   и тем самым зададим нечеткое соответствие  между множествами  и .

На следующем шаге построим свертку  в виде композиции соответствий , причем результирующее отношение  определяется как произведение , , . То есть, получается единое результирующее отношение, определенное с учетом информации об относительной важности нечетких отношений предпочтения . С отношением  ассоциируются  отношение  и множество . Корректируется множество  до множества   с функцией принадлежности:

.

Выбирается та альтернатива, для которой значение функции принадлежности, скорректированного нечеткого множества  недоминируемых альтернатив максимально. Достоинством рассмотренных способов (алгоритмов ) решения задачи c областью определения (5) в условиях нечеткости процессных данных является простота их программной реализации.

Заключение

Рассмотренные в работе задачи и методы нечеткой идентификации и нечеткого мониторинга процессных рисков проекта расширяют практические области эффективного применения формальных методов для решения основных задач управления процессными рисками проектов в условиях нечеткости исходных данных. При этом достаточно простая программная реализация предложенных методов позволяет эффективное использование созданного специального инструментария в составе интегрированных автоматизированных технологий управления проектами.

Литература

1. ANSI/PMI 99-001-2004. Руководство к Своду знаний по управлению проектами. Четвертое издание (Руководство PMBOK).

2. Таганов А.И. Методика анализа и сокращения рисков проектов сложных программных систем по характеристикам качества // Вестник РГРТУ. - Рязань, 2010. - Вып. 30. - С. 77-82.

3. Фатрелл Р.Т., Шафер Д.Ф., Шафер Л.И. Управление программными проектами: достижение оптимального качества при минимальных затратах: пер. с англ. - М.: Вильямс, 2003. - 1136 с.

4. Гильман Д.В. Использование нечеткого вероятностного графа для оценки показателя надежности проекта // В сб. трудов Всероссийской научно-технической конференции «Новые информационные технологии в научных исследованиях и в образовании». – Рязань: РГРТУ, 2010.

5. Мелихов А.Н., Бернштейн Л.С., Коровин С.Я. Расплывчатые ситуационные модели принятия решений.- Таганрог:ТРТИ, 1986. -92 с.

6. Андрейчиков А.В., Андрейчикова О.Н. Системный анализ и синтез стратегических решений в инноватике. Математические, эвристические и интеллектуальные методы системного анализа и синтеза инноваций. – Издательство: Книжный дом «Либроком», 2012. 304 с.