Байрамукова Е.И.

К вопросу построения модели социально-экономического развития региона

Анализ различных математических моделей применительно к исследованию развития и функционирования социально-экономических систем различного типа показывает, что для этих целей достаточно удобно использовать аппарат дискретной  математики, в частности знаковых, взвешенных знаковых и функциональных знаковых графов. Аппарат позволяет работать с данными как качественного, так и количественного типа, причем степень использования количественных данных может увеличиваться в зависимости от возможностей количественной оценки взаимодействующих факторов в итерационном цикле моделирования. На первоначальном этапе происходит сбор сведений об изучаемой социально-экономической системе (ситуации). Затем формулируются определенные концепции и допущения относительно системы и на строгом математическом языке  формируется математическая модель, позволяющая оценить динамику поведения (развития).

Аппарат знаковых графов позволяет формально строить прогнозы развития или траектории движения моделируемой системы в фазовом пространстве ее переменных (факторов) на основе информации о структуре и программах её развития, путем аппроксимации их кусками траекторий импульсных процессов на знаковых орграфах [1].

В модель включаются следующие компоненты [2]:

1) Множество параметров вершин. Каждой вершине из их множества X может быть приписан набор параметров V.

2) Функционал преобразования дуг F (V, Е), ставящий в соответствие
каждой дуге либо знак, либо вес, либо функцию.

Если функционал имеет вид:

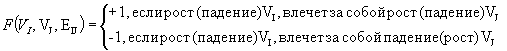       ,        (1)

то такая модель является знаковым орграфом.

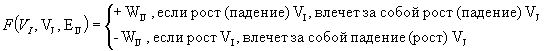      , (2)

то такая модель является взвешенным знаковым орграфом. Здесь  является весом соответствующей дуги.

Если функционал имеет вид:

                                 ,                                                     (3)

то такая модель является функциональным знаковым орграфом.

На расширенных таким образом орграфах вводится понятие импульса и импульсного процесса в дискретном временном пространстве. Импульсом  в вершине , в момент времени  называется изменение параметра в этой вершине в момент времени :

При этом новое значение параметра в вершине  будем определять соотношением:

                                                  (5)

Здесь  — внешний импульс, вносимый в вершину  в момент времени . Из конечно-разностных уравнений (4) и (5) легко получить уравнение для импульса в исследуемом процессе:

                             .                                  (6)

Аппарат знаковых графов представляет собой мощное средство структурного моделирования. Моделирование позволяет проводить исследование тенденций развития экономики всей страны, отдельного региона, края, отраслей и т.д. Однако с помощью этого аппарата можно также планировать внесение в СЭС (социально-экономическая система) определенных управляющих воздействий для достижения необходимых тенденций стабилизации и развития. При решении этой задачи можно определить набор вершин, в которые следует вносить управляющие воздействия, приводящие к необходимому результату, а также характер этих воздействий. Эти данные являются основой для построения детальных планов управления СЭС. Таким образом, от традиционных задач для этого аппарата моделирования («что будет, если») мы переходим к решению более содержательной задачи: «что надо сделать для достижения заданного поведения системы».

Формализуем задачу об оптимальном управлении применительно к аппарату знаковых орграфов. Для этого из множества вершин выделим две: вершину-объект и вершину-субъект. Вершина-объект — та вершина, изменение которой мы хотим контролировать на заданном временном интервале. Вершина-субъект — вершина, влиянием на которую обеспечивается контролируемое изменение. В соответствии с этими предположениями изменение параметра вершины-объекта задается уравнением [3]:

                             ,                                               (7)

где - измененный параметр вершины,

- параметр вершины без импульса,

- первоначальный импульс,

- задаваемый импульс.

Если необходимо обеспечить невозрастание параметра вершины-объекта, то вводятся ограничения:

                                                                                                   (8)

Аналогично можно обеспечить неубывание этого параметра. Из системы линейных алгебраических неравенств (8) можно найти — набор внешних импульсов, вносимых в вершину-субъект. В качестве критерия оптимальности найденного решения выберем его минимальную стоимость. Пусть заданы  — «стоимость» единицы внешнего импульса, посылаемого в вершину-субъект. В этом случае решение системы, (8) удовлетворяющее критерию оптимальности:

                                                                                             (9)

Использование предлагаемой системы показателей в процессе мо­делирования даст возможность определения функциональных зави­симостей между выбранными показателями и, как следствие, для объективной оценки потенциала региона.

Решение этой обратной задачи позволит перейти от прогнозирования поведения социально-экономической системы к планированию действий по ее управлению. При выборе субъектов управления необходимо заметить, что в их качестве могут выступать только реальные рычаги управления, а в качестве программы внешних воздействий — имеющиеся в наличии ресурсы. Полученная программа внешних воздействий может быть преобразована в конкретный план управления. Причем в процессе моделирования делается вывод о том, насколько продолжительно может быть это управление для обеспечения необходимых целей:

- разовое, т. е. внесение одного импульса полностью и навсегда устанавливает необходимую тенденцию;

- временное, необходима программа воздействий в течение ограниченного периода времени и затем навсегда устанавливается необходимая
тенденция;

- постоянное, необходимо постоянное управление для обеспечения желательной тенденции.

Формирование модели социально-экономического развития должно базироваться, в первую очередь, на оценке предлагаемых структур и взаимосвязей базовых факторов  по степени их соответствия принципу соразмерности ее элементов, предусматривающему сбалансированность различных составляющих социально-экономического развития. Выбор точек и характера воздействия на формирование социально-экономической модели являются исключительно сложными задачами, решение которых должно базироваться на комплексе методов многофакторного  моделирования. Анализ текущих и рассмотрение будущих траекторий развития социально-экономических параметров и составляющих ее элементов на основе оценки тенденций экономического развития на определенный период является важнейшей задачей для краевых органов власти и управления.

Определение характера и точек внесения управляющих воздействий — это начальный этап разработки детальных планов управления. Однако для привязки этих планов к конкретным условиям необходимо знать, когда надо их вносить. Задача состоит в определении времени влияния на СЭС для достижения определенных целей. Поскольку аппарат знаковых графов может дать только качественный результат, то время в данном случае определяется не как физическая величина, а как последовательность наступления событий.

Процесс моделирования происходит следующим образом. На каждом шаге происходит снятие данных с вершин мониторинга для идентификации ЭЗС. При успешной идентификации ЭЗС происходит расчет первой по приоритету программы управления. Если ее расчет невозможен, то выбирается для расчета следующая ситуация и т. д. После получения программы управления происходит внесение управляющих воздействий в модель СЭС. Последовательность наступления событий представляет собой сценарий поведения СЭС, а последовательность внесения управляющих воздействий — сценарий управления.

Результаты моделирования процессов поведения факторов, формирующих модель, определяются взаимодействием базовых социально-экономических процессов и факторов, действующих на процесс её формирования. При этом взаимовлияния базисных процессов могут образовывать циклы обратных связей, а взаимодействия циклов вызывать либо нарастающие колебания факторов, либо резкое монотонное усиление их – резонанс.

Результаты функционирования составляющих системы определяются большим числом переменных, взаимодействующих друг с другом, реагирующих с разной чувствительностью по отношению к изменениям окружающих переменных. Поэтому при математическом моделировании процесса функционирования сис­темы с целью выработки предложений по его совершенствованию воз­никает необходимость нахождения компромисса между точностью ре­зультатов моделирования и возможностью получения достоверной информации о динамике изменения фак­торов, необходимой для построения адекватной модели.

Моделирование взаимовлияния базовых фак­торов системы друг на друга рассматривается как попытка, во-первых, отобразить  взаимовлияние базовых факторов, которые оказывают как прямое, так и косвенное влияние на составляющие систему  параметры. Во-вторых, дополнить данную модель факторами макроэкономического и социального уровня.

Таким образом, алгоритм построения модели социально–экономического развития системы региона можно представить в виде схемы (рис. 1).

Рис. 1 – Алгоритм построения модели социально-экономического развития системы региона

Литература:

1. Глущенко В.В. Прогнозирование. 3-е издание. – М.: Вузовская книга, 2000. – 208 с.

2. Глущенко В.В., Глущенко И.И. Разработка управленческого решения. Прогнозирование-планирование. Теория проектирования экспериментов. -Железнодорожный, Моск.обл.: ТОО НПЦ «Крылья», 2007. – 400 с.

3. Горелов С. Математические методы в прогнозировании. – М.: Прогресс, 2003.