Хотомлянский А.Л., Черната Т.Н., Деревянко Т.А.

Модель распространения поражающих возмущений в производственных системах

Возмущения на входе производственной системы либо ее элементов передаются другим сопряженным элементам. При этом остается мало исследованным сам механизм распространения поражающих возмущений, приводящих к потере устойчивости сложных систем.

В отличие от технических систем, каждый элемент которой, как правило, описывается ограниченным перечнем унифицированных показателей (например, долговечностью или безотказностью в работе),  в производственных системах используется широкая номенклатура показателей, зависящая от роли и назначения структурного подразделения, а также  его места в общей схеме производственного процесса. Показатели могут быть как простыми (первичными), отражающими ресурсный потенциал системы и ее элементов, так и более агрегированными (сложными), являющиеся производными простых показателей.

В рассматриваемом контексте интерес представляют характеристики, изменение которых может оказать влияние на состояние сопряженных элементов системы. К числу таких характеристик можно отнести  показатели объемов деятельности, производственной себестоимости, качества продукции (услуг), ритмичности производства и др. Конкретный состав характеристик будет зависеть от отраслевой принадлежности производственной системы, а также роли и назначении элементов системы.

               Для описания распространения  возмущений импульсного типа в производственных системах воспользуемся обозначениями, приведенными в работе [2], представив производственную систему  в виде конечного графа , где  - множество вершин, а , - множество ребер. Каждой вершине и ребрам  графа приписываются количественные и качественные характеристики (показатели).

         На орграфе  возмущение, возникшее в вершине , будет передаваться вершине  i≠j по входящим в нее ребрам . Сохранившаяся доля передаваемого возмущения ∆_iпри переходе от вершины   ориентированного ребра графа к вершине  будет определяться по выражению:

∆_j= K_ij*∆_i                                                        (1)

где К_ij- передаточный коэффициент, характеризующий степень влияния i –го элемента системы на сопряженный с ним j –й элемент при импульсном возмущении определенной характеристики (0≤К_ij≤ 1).

          Если в вершину графа  входит   m ребер, то сохранившаяся доля передаваемого воздействия будет определяться по выражению:

               Для  определения передаточных функций могут использоваться детерминированные (расчетные) либо статистические методы. Выбор конкретного метода определяется природой показателя и особенностями организации производства.

               Так, для определения передаточной функции по показателю объема производства продукции могут привлекаться расчетные методы. Обозначим через ∆Q_i  отрицательное  возмущение в объемах выпуска продукции с точкой приложения в вершине i, которое будет передаваться вершине j. При отсутствии буферных емкостей (т.е. при жестких связях между вершинами) отрицательное  импульсное возмущение ∆Q_i  приведет к простоям ∆T_j=  в работе основного оборудования  j -го структурного подразделения, где  P_i - производительность основного оборудования в единицу рабочего времени. Тогда ∆Q_j= ∆T_j* P_j, а коэффициент передачи .

При наличии буферной емкости Ω_ijмежду вершинами ij К_Q= 0, если ∆Q_i  ≤ Ω_ij.Если ∆Q_i≥ Ω_ij, то величина передаваемого возмущения будет равна              ∆Q_i' = ∆Q_i- Ω_ij,  ∆T_j=,   ∆Q_j= *P_j. При этом .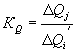

Наряду с расчетными методами определения коэффициентов передачи могут привлекаться статистические методы, применение которых показано в работе [3].

Знание количественных взаимосвязей между элементами системы служит основой для поиска компенсаторов возмущений, их блокирования  либо локализации поражающего воздействия.

Литература:

1.Кочкаров А.А. и Малинецкий Г.Г.Обеспечение стойкости сложных систем. Структурные аспекты. ИПМ им. М.В.Келдыша. РАН, Москва, 2005.

2.Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И.Лекции по теории графов. - М.: Наука, 1990.

3.Хотомлянский А.Л., Черната Т.Н.Статистический анализ взаимосвязи результатов производственной деятельности технологически сопряженных цехов металлургического комбината. //Известия высших учебных заведений. Черная металлургия. - №5. - 2004, С.70-73.