Катаргин Н.В., к.т.н. Богомолов А.И., к.т.н. Костюнин В.И.

Сравнение оценки стоимости опциона по модели Блэка-Шоулза и методом Монте-Карло

где

Цена (европейского) опциона put:

     Основная цель данной работы – продемонстрировать, как может изменяться возможная прибыль, связанная с владением опционом, в зависимости от волатильности цены базового актива и страйка. Для этого мы многократно (по 1000 раз) имитировали движение цены акции в течение 5 лет (60 месяцев) с шагом 1 месяц при годовой волатильности 10%, 20% и 30%. Предполагалась модель случайного блуждания цены

S(t) = S(t-1) + S(0) σ R

где S(0)– цена в начальный период времени, σ–месячная волатильность в процентах, R– случайная величина, нормально распределенная в диапазоне -3…+3. При каждой имитации определялось максимальное и конечное значение цены в течение 5 лет, которые сохранялись в памяти компьютера. Для каждого значения волатильности проводилось 1000 имитаций. Работа проводилась в среде Excel  с использованием Visual Basic. Некоторые имитации временных рядов цен представлены на Рисунке 1.

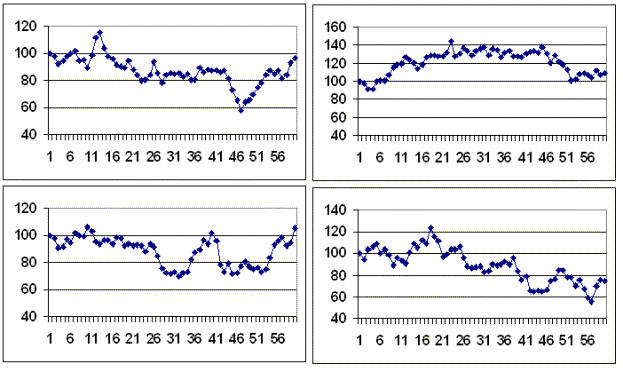
Рис. 1. Имитации движения цены базового актива в течение 5 лет; σ =20 %.

На Рисунке 2а представлена гистограмма частот максимумов цен базового актива. Видно, что распределение асимметричное и близко к логнормальному.

Рис. 2.  Частотное распределение максимумов цен базового актива (а)  и цен в конце срока 5 лет (б); S(0)=100, σ =20 %.

         Возникает вопрос – как использовать полученные временные ряды для оценки стоимости опциона call. Максимальный выигрыш, который может получить владелец американского опциона, равен разности максимальной цены акции в течение периода действия опциона и страйка. Из этой величины придётся вычесть и стоимость опциона. Максимальный проигрыш равен цене опциона, так как владелец опциона не обязан выкупать акцию, если её цена упала ниже страйка. Возможны два способа оценки возможного выигрыша:

I.  Вычислить среднее значение величины ( maxS(t) – страйк)  повсем сгенерированным временным рядампри заданных значениях страйка  и волатильности (американские опционы).

 II. Вычислить ту же величину, отбрасывая отрицательные значения       ( maxS(t) – страйк) , т.е. акции с максимальной ценой ниже страйка не выкупаются (американские опционы).

III. Вычислить среднее значение величины ( S(5 лет) – страйк) повсем сгенерированным временным рядампри заданных значениях страйка  и волатильности,   отбрасывая отрицательные значения (европейские опционы).     

В Таблице 1 представлены результаты расчётов по этим моделям, а также по модели Блэка-Шоулза (Б.-Ш.) при тех же параметрах и без учёта дисконта (r=0). При страйке 100 модели I и II совпадают, так как        maxS(t) ≥ S(0) = 100.

По результатам расчётов можно сделать некоторые выводы:

1. Доходы, вычисленные по моделям I и II, примерно пропорциональны ценам опционов, вычисленным по модели Блэка-Шоулза, и превышают их в 1,5 раза, кроме случая: Модель I, страйк 120, σ =10 %. Так и должно быть, так как для получения максимального дохода владелец опциона должен угадать максимум цены акции, причём не локальный, а по всему временному ряду. При вероятности правильного угадывания 35 % есть шанс вернуть деньги, потраченные на приобретение опциона.

2. Доходы, вычисленные по модели III, примерно совпадают с ценами опционов, вычисленных по модели Блэка-Шоулза.

3. Метод Монте-Карло позволяет наглядно демонстрировать зависимость дохода владельца опциона в зависимости от волатильности базового актива, страйка и времени действия опциона, что может быть полезным при обучении студентов.

                                                                                                       Таблица 1.

Литература.

1. Д. Лоуренс, Г. Макмиллан.  Опционы как стратегическое инвестирование. Изд. дом «Евро», 2005.