Алдажаров К.

Кинетика и динамика непрерывного процесса торговли

В большой системе, какой является экономика, переходные процессы длятся годами и рынок переходит из одного устойчивого состояния в другое через дефицит  или перепроизводство товаров, инфляцию или недостаток денег.

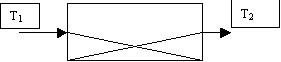                                  Рис.1. Схема стационарного рынка

  Условие стационарности требует соответствия распределений денег и товаров. Функция распределения товаров остается неизменной, деньги же приспосабливаются путем изменений цен.

  Наоборот, при снижении потока Д₁ на  входе цена товара снижается. Прибыль при этом также уменьшается, происходит перетекание капитала в более выгодные отрасли и наконец, через достаточное большое  время спрос и предложение снова приходят в равновесие через регулятор – рынок.

       Известно, что структура потоков оказывает существенное влияние на эффективность торгово - финансовых процессов, поэтому ее необходимо учитывать при моделировании рыночных процессов. При этом математические модели структуры потоков являются основой, на которой строится математическое описание  торгового процесса.

     При проведении торгов часто важно знать степень полноты  их завершения,  что, в свою очередь зависит от  распределения по времени пребывания торговых агентов на рынке, поскольку некоторая часть их может задерживаться на рынке, а другие, наоборот, "проскакивать", что непосредственно связано с временем контакта и "диффузией". Распределение времени пребывания торговых агентов на рынке имеет стохастическую природу и оценивается статистическим распределением.

     Рассмотрим более подробно систему одностадиального цикла процесса торгов и влияние  периодических изменений  величины входного потока на распределение плотности наполнения рынка товарами и деньгами. За начала отсчета примем такую плотность наполнения, при превышении которой масса денег и товаров приводит к инфляции. Поток Qнекоторого вида товаров Uчерез данное сечение рынка пропорционален градиенту плотности наполнения. Сопоставляя время t торгов с продвижением x от входа к выходу из рынка можно написать:

Явления, подчиняющиеся такому закону, описываются уравнением диффузии

Изменение плотности в данном сечении рынка равно разности втекающих и вытекающих потоков. Поток втекающий на рынок обозначим  A(1+m sin ω t); поток, направленный из рынка, будем считать пропорциональным плотности наполнения рынка во входной точке. Тогда граничные условия запишутся:

Обычно за начальное условие принимают или нулевое или установившееся значение исследуемой величины (для достаточно продолжительных процессов это безразлично). Запишем начальные условия в форме

Нашу однородную задачу с ненулевыми граничными и начальными условиями приведем к неоднородной  с нулевыми граничными и начальными условиями. Для этого введем новую функцию V(x, t):

Тогда новые граничные условия запишутся так:

Соответствующие начальные условия будут:

Уравнение примет вид:

где

Решение в соответствии с граничными условиями будем искать в виде ряда Фурье:

Окончательное решение нашего уравнения после преобразований и соответствующих подстановок будет:

где  

Коэффициенты при cos ωt и sin ωt определяют скорость нарастания и спада плотности наполнения рынка при периодическом изменении величины входного потока. Соответствующим выбором частоты возмущений ω, а следовательно γ, можно получить быстрое затухание амплитуды колебаний по объему рынка.

     Приведенный анализ позволяет выработать условия сглаживания случайных колебаний курса валют, цен на зерно, продуктов переработки и др.