Стохастический тренд индекса ПФТС

Основными индикаторами фондового рынка являются индексы, рассчитываемые на основании котировок определенной группы ценных бумаг. В зависимости от того, какие компоненты содержит индекс, он может отражать поведение определенной группы акций или всего фондового рынка. Индекс Украинского фондового рынка ПФТС (первая фондовая торговая система) признан международной финансовой корпорацией (МФК) как единственный индекс, используемый этой организацией при мониторинге внутреннего состояния украинского фондового рынка. Индекс определяет средний уровень наиболее ликвидных украинских акций, которые имеют наибольшую рыночную капитализацию. Информацию о состоянии индекса ПФТС публикует на своем сайте «Первая фондовая торговая система», которая представляет собой электронную биржу ценных бумаг Украины и поддерживает работу национальной электронной системы торговли ценными бумагами в режиме «online».

Большинство математико-статистических методов имеет дело с моделями, в которых наблюдения предполагаются независимыми и одинаково распределенными. При этом основное внимание уделяется проблемам идентификации моделей, отбору эндогенных и экзогенных показателей, но почти не обращается внимания на формальный анализ структуры исходных статистических рядов. Зависимость между наблюдениями чаще всего рассматривается как помеха в эффективном применении этих методов. Однако разнообразные данные в экономике, социологии, финансах, коммерции и других сферах человеческой деятельности поступают в форме временных рядов, в которых наблюдения взаимно зависимы, и характер этой зависимости как раз и представляет главный интерес для исследователя. Принципиальные отличия временного ряда от последовательности наблюдений, образующих случайную выборку, заключаются в следующем:

- в отличие от элементов случайной выборки члены временного ряда не являются независимыми;

- члены временного ряда не обязательно являются одинаково распределенными.

Аналитически временной ряд можно выразить уравнением вида:

Где - тренд ( долговременная тенденция ) развития;

- случайная величина ( случайный компонент ).

Функция определяет общую тенденцию развития изучаемого явления. Тренд может быть выражен как детерминированной, так и случайной функциями, либо их комбинацией. Компоненты временного ряда , и не наблюдаемы, они являются теоретическими величинами. Выявление этих компонент и является задачей анализа. В рядах с детерминированным трендом влияние предыдущих шоковых воздействий (резких изменений) затухает с течением времени, а в рядах со стохастическим трендом такое затухание отсутствует, и каждый отдельный шок влияет с одинаковой силой на последующие значения ряда. Такие ряды называют «временные ряды с долговременной корреляционной зависимостью» (time series with long memory) или «ряды с долговременной памятью». Каждое наблюдение таких рядов коррелирует до некоторой степени с последующими наблюдениями, а для корреляционной функции характерно медленное убывание. Детерминированные компоненты и обнаруживается с помощью спектральнго анализа [1]. Детерминированная составляющая имеет неограниченную спектральную плотность на низких частотах, а при наличии периодических составляющих спектральная плотность имеет максимумы (пики). Основанием для гипотезы о наличии долговременной

памяти является значение коэффициента Херста , который получают в результате анализа [2]. Процедура проверки гипотезы по статистике подробно описана в [3].

Благодаря развитию компьютерных технологий созданы программы, с помощью которых выполняют анализ. Одна из них Fractan 4.4. Эта программа распространяется бесплатно и помещена на многих Internet-сайтах, например, http://soft.softodrom.ru/Fractan-p44195. Однако, для расчетов в пакете Fractan требуется не менее трех тысяч эмпирических данных. Методика, описанная в [4], не требует большого числа данных, а результаты, полученные по этой методике статистически более значимы.

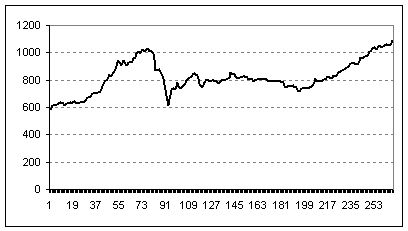
На Рис. 1 представлены данные динамики индекса ПФТС за 2010 год. Коэффициент Херста равен , гипотеза о наличии долговременной памяти принимается с вероятностью при значении статистики . Аналогичный результат получен по данным за все годы периода с 2000г. по 2010г. Следовательно, индекс ПФТС имеет стохастический тренд.

В настоящее время особую популярность для анализа и прогнозирования временных рядов приобретают приложения – нейроимитаторы, использующие нейронные сети различных архитектур. Например, свободно распространяемые - NeuroPro и NeuroShell (http://www.orc.ru). NeuroPro 0.25. Пакеты содержат программу, надстройку Excel, которая дает возможность применять нейронные сети из рабочих листов Excel [4].

Для индекса ПФТС была применена нейронная сеть Элмана в имитаторе NeuroPro 0.25, поскольку она способна помнить свои предыдущие действия и реализовывать задачи обучения, разворачивающиеся во времени, что актуально для прогнозирования временных рядов с памятью. На Рис.2 показаны результаты моделирования и прогнозирования на 20 дней вперед с помощью нейроимитатора NeuroPro 0.25. Черным цветом обозначены фактические данные, серым – прогнозные.

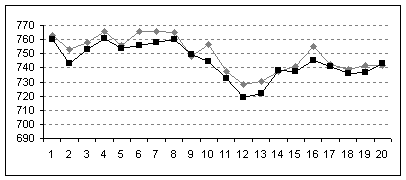
Рис.2. Результат прогнозирования.

Из рисунка видно, что модель полностью отражает тенденцию фактических данных, при этом среднеквадратическая ошибка . Таким образом, можно считать модель адекватной, а прогноз удовлетворительным.

Наличие стохастического тренда свидетельствует об инерционности фондового рынка. Это дает возможность под другим углом взглянуть на работу рынка и методологию оценки рисков.

Литература

1. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и управление/ Дж.Бокс, Дженкинс Г. - Вып. 1, 2 - М.:Мир, 1974.-197с.

2. Петерс Э. Фрактальный анализ финансовых рынков. М.: Интернет- трейдинг, 2004. - 304с.

3. Lo A.W. Long Term Memory in Stock Market Prices/ A.W.Lo //Econometrica.-1991.-№59.-P.1279-1313.

4. Хайкин С. Нейронные сети: полный курс, 2-е изд., испр./ Хайкин С. Пер. с англ. – М.: ООО “И.Д. Вильямс“, 2006. - 1104 с./ Под ред. д.т.н. Н.Н. Куссуль.