Методика исследования характеристик сложных организационно-технических систем, функционирующих в конкурентной среде в условиях риска

Структурная сложность рассматриваемой СОТС и особенности ее функционирования предопределяют невозможность использования традиционных подходов, которые, в большинстве случаев, не учитывают условия стохастической неопределенности, риска или параметрической неопределенности моделей систем. Разработана методика мониторинга текущих предприятия, функционирующего в конкурентной среде в условиях риска.

Для построения математической модели процесса функционирования СОТС воспользовались научно-методическим аппаратом теории марковских процессов [2,3]. Классифицированы m подсистем типовой подобной СОТС и определены все возможные ее состояния. Под требуемым состоянием функционирования СОТС подразумевается то ее состояние, которое соответствует требованиям нормативно-технической документации (НТД) и реализуется без нарушений и сбоев. Под нежелательным состоянием – то состояние, когда процесс функционирования имеет отклонения от условий, указанных в НТД. Нежелательные состояния СОТС возникают вследствие j-х внешних или внутренних случайных воздействий, а устранение последствий таких воздействий с целью возвращения СОТС в состояние S0 осуществляется на основе i-го алгоритма (, ). Таким образом, для каждого j-го нарушения имеется n возможных алгоритмов направленных действий. Граф состояний в этом случае имеет вид, показанный на рис. 1.

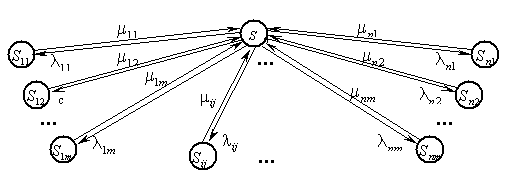
Рис. 1. Граф состояний СОТС

Интенсивности (рис. 1) возникновения внешних или внутренних случайных воздействий, приводящих к нарушениям функционирования СОТС и, соответственно, к переходам ее из требуемого состояния в любое нежелательное неизвестны. Этот факт и обуславливает неопределенность функционирования СОТС. В то же время, интенсивности восстановлений известны.

В общем случае подобные задачи теории марковских процессов решаются на основе использования систем дифференциальных уравнений Колмогорова. Но в силу того, что интенсивности lij неизвестны, система дифференциальных уравнений Колмогорова является параметрически неопределенной. Поэтому потребовалась идентификация в реальном времени значений интенсивностей , характеризующих текущее состояние СОТС, для чего воспользовались формализмом теории игр.

В силу особенностей рассматриваемого объекта объем статистической информации для данной задачи традиционно недостаточен, а количество реализаций невелико. Поэтому воспользовались наиболее распространенным в подобных случаях критерием Ходжа-Лемана (ХЛ) :

Где – функция выигрыша первого игрока, соответствующая антагонистической игре с матрицей A, в которой оптимальность смешанных стратегий первого игрока понимается в смысле критерия Ходжа-Лемана, b – параметр критерия ХЛ, , – множества смешанных стратегий, xi – вероятность выбора первым игроком i-й чистой стратегии, hj – вероятность выбора вторым игроком j-й чистой стратегии, lij – интенсивность возникновения внешних или внутренних случайных воздействий.

В случае применения критерия ХЛ может обеспечиваться ориентация как на средний результат (при коэффициенте b, близком или равном 1), так и на получение наилучшего гарантированного результата (при коэффициенте b, близком или равном 0). Для определения использована модель смешанного расширения матричных игр неклассического типа [2].

В синтезированной методике, таким образом, реализуется подход комбинированного использования теории игр и теории марковских процессов, позволяющий идентифицировать текущие характеристики технико-экономической подсистемы обеспечения жизнедеятельности предприятия, функционирующего в конкурентной среде в условиях риска.

Литература:

1. Охтилев М.Ю. и др. Интеллектуальные технологии мониторинга и управления структурной динамикой сложных технических объектов. М.: Наука, 2006. 410с.

2. Строцев А.А., Синицын С.В., Кузьменко А.Н. Методика оценки эффективности применения модели смешанного расширения матричных игр неклассического типа к задачам контроля технического состояния сложных систем // Радиоэлектроника. Известия ВУЗов. 2009. – Т. №50, №7.

3. Строцев А. А. Модифицированный метод Брауна решения матричной игры "неклассического" типа // Экономика и математические методы. - 2001. - Т. 37, N 3.