Паламарчук А.А. Автомобильно-дорожный институт ГВУЗ «ДонНТУ»
Математическое моделирование прецедентов системы «Заключение депозитного договора в коммерческом банке»
В настоящее время начинает получать широкое распространение новый метод научного исследования – математическое моделирование систем. Это практически единственный метод решения научных задач особой сложности, особенно задач, которые возникают при создании систем централизованного управления коммерческим банком [1]. Метод сводится к построению математической модели, позволяющей представить систему или процесс, и проведению экспериментов на модели.
Целью статьи является построение математической модели прецедентов виртуальной системы «Заключение депозитного договора в коммерческом банке», используя понятия универсальной алгебры конечных предикатов.
Для усовершенствования организационной структуры банка была создана виртуальная модель диаграммы состояний системы. Виртуальная модель имеет такие преимущества перед фактической системой:
1) Уменьшение персонала в составлении депозитного договора: теперь расчет процентов по депозитным договорам и проверку правильности заполнения договора выполняет «Депозитный эксперт», а «Операционист» извлечен из процесса проведения депозитных операций. Это позволяет снизить затраты Банка на оплату труда наемных рабочих.
2) Уменьшились затраты времени «Физического лица» на заключение депозитного договора, т.к. он не взаимодействует с «Бухгалтерией» (теперь «Касса» за малый отрезок времени по электронной почте связывается с «Бухгалтерией» и запрашивает регистрацию депозитного счета). Эти качества достигнуты за счет модернизации и инновационного внедрения в сферу деятельности Банка компьютеризации отдельных структур и отделов. Данные изменения в системе позволят привлечь больше клиентов-вкладчиков депозитов.
3) Извлечение из процесса проведения депозитных операций специальных карточек, т.к. их использование нецелесообразно (они являются лишней документацией, которая требует дополнительных затрат).
Таким образом, фактическая система упрощена, получила новые качества в быстроте обработки данных, лишена доли вероятности возникновения ошибок в процессе её работоспособности.
В результате объектного анализа состояний системы «Заключение депозитного договора в коммерческом банке» получены виртуальные диаграммы состояний системы для следующих сценариев рассматриваемого прецедента – «Виртуальный основной», альтернативный виртуальный поток событий «Есть ошибки в заполнении депозитного договора», альтернативный виртуальный поток событий «Обнаружены фальшивые деньги».
Алфавит букв для данной системы:
А = {a11,1, a12,1, a13,1 , a14,1, a15,1 , a16,1 , a17,1, …, a310,4 , a311,4 , a312,4},
где первый нижний индекс – это номер состояния объекта, второй нижний индекс – это номер объекта, верхний индекс – номер сценария.
Множество переменных следующее: В = {x1, x2, x3, x4}, соответственно объектам системы.
Введен алфавит букв: S = {S1, S2, S3}. Элементы данного алфавита ассоциированы с математическими моделями сценариев системы «Заключение депозитного договора в коммерческом банке».
Образовав дизъюнкцию элементов алфавита букв S и, приравняв ее к единице, получена математическая модель прецедента в виде уравнения алгебры конечных предикатов:
![]() .
.
Т.к. элементы алфавита букв S ассоциированы с математическими моделями сценариев системы, то данное уравнение можно записать в виде:
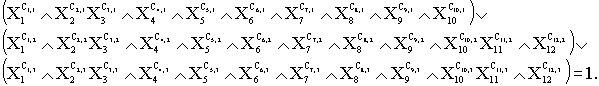
Конъюнктивные члены левой части уравнения являются конституантами единицы, следовательно, показатели узнавания предикатов являются решениями уравнения, содержательная интерпретация которых содержится в том, что реализация прецедента возможна по одному из допустимых сценариев [2].
Таким образом, полученные результаты в дальнейшем могут использоваться для оптимизации работы системы «Заключение депозитного договора в коммерческом банке». Модель прецедентов позволяет описать процесс на концептуальном уровне и не только изучить систему, но и построить ее виртуальный образ [3].
Литература Васюренко О.В. Банківські операції: навч. посібник / О.В. Васюренко. – К.: Знання, 2002. – 255 с. Никольская И.Л. Математическая логика: учебник / И.Л. Никольская. – М.: Высшая школа, 1981. – 127 с. Шабанов-Кушнаренко Ю.П. Теория интеллекта / Ю.П. Шабанов-Кушнаренко. – Х.: Высшая школа, 1984. – 144 с.
