Дмитренко И.С. Донбасская государственная машиностроительная академия
Моделирование спроса и потребления в маркетинге в практических задачах по курсу исследования операций
Основными задачами и функциями маркетинга является управление рыночной системой производственной и сбытовой деятельности предприятия, при которой в основе принятия хозяйственного решения лежит рыночная информация, а обоснованность решений проверяется рынком в ходе реализации товаров и услуг. При таком подходе начальным пунктом всего цикла предпринимательской деятельности становится изучение потребительского спроса.
Уровень удовлетворения материальных потребностей общества можно выразить целевой функцией потребления ![]() , где вектор
, где вектор ![]() включает разнообразные виды товаров и услуг. Свойства этой функции удобно изучать, используя геометрическую интерпретацию уравнений
включает разнообразные виды товаров и услуг. Свойства этой функции удобно изучать, используя геометрическую интерпретацию уравнений ![]() , которые в маркетинге носят название кривых безразличия, представляя собой линии уровня целевой функции. Среди основных свойств целевой функции, учитывающихся при построении соответствующих математических моделей, стоит выделить следующие свойства: Функция
, которые в маркетинге носят название кривых безразличия, представляя собой линии уровня целевой функции. Среди основных свойств целевой функции, учитывающихся при построении соответствующих математических моделей, стоит выделить следующие свойства: Функция ![]() является возрастающей функцией всех аргументов, т.е. увеличение потребления любого блага при неизменном уровне потребления всех других благ увеличивает значение данной функции. Кривые безразличия (линии уровня) не могут пересекаться, т.к. в противном случае один и тот же набор благ одновременно соответствовал бы нескольким разным уровням материального благосостояния. Кривые безразличия являются выпуклыми вверх кривыми.
является возрастающей функцией всех аргументов, т.е. увеличение потребления любого блага при неизменном уровне потребления всех других благ увеличивает значение данной функции. Кривые безразличия (линии уровня) не могут пересекаться, т.к. в противном случае один и тот же набор благ одновременно соответствовал бы нескольким разным уровням материального благосостояния. Кривые безразличия являются выпуклыми вверх кривыми.
В качестве примера приведем квадратичную целевую функцию потребления для трех агрегированных групп товаров, построенную на основе обработки данных бюджетной статистики (пример взят из [2]):
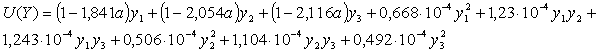
где параметр a обозначает число детей в семье, y1- потребление продуктов питания, y2- потребление промышленных товаров, y3- потребление платных услуг. На практических занятиях в высшей школе, естественно приводить примеры, имеющие хорошую наглядную геометрическую интерпретацию и допускающие применение классических методов математического анализа.
Рассмотрим один из примеров, иллюстрирующий рассмотренную маркетинговую модель, в двухмерной постановке.
Уровень удовлетворения материальных потребностей некоторой семьи характеризуется целевой функцией потребления ![]() где
где ![]() - потребление продуктов питания,
- потребление продуктов питания, ![]() - потребление промышленных товаров, включая услуги. Составить функции спроса на товары I и II группы от дохода
- потребление промышленных товаров, включая услуги. Составить функции спроса на товары I и II группы от дохода ![]() , считая доход переменным фактором, если цены на товары I и II группы остаются неизменными и равны
, считая доход переменным фактором, если цены на товары I и II группы остаются неизменными и равны ![]() и
и ![]() денежных единиц соответственно. Построить графики полученных функций спроса на товары I и II группы в зависимости от дохода
денежных единиц соответственно. Построить графики полученных функций спроса на товары I и II группы в зависимости от дохода ![]() . Выяснить, как изменится спрос на товары I и II группы, если доход семьи возрастет от
. Выяснить, как изменится спрос на товары I и II группы, если доход семьи возрастет от ![]() до
до ![]() денежных единиц. Для решения задачи применим метод классической оптимизации - метод множителей Лагранжа.
денежных единиц. Для решения задачи применим метод классической оптимизации - метод множителей Лагранжа.
Составим функцию Лагранжа для данной задачи:
Необходимым условием экстремума функции Лагранжа является равенство нулю частных производных первого порядка по всем переменным:
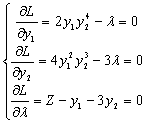
![]()
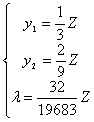
Таким образом, на приобретение продуктов питания семья тратит в среднем 33% дохода, а на промышленные товары с услугами около 22% денежных единиц от общего дохода.
Проведем геометрический анализ результатов решения. Построим графики полученных функций спроса на товары I и II группы в зависимости от дохода ![]() (рис.1).
(рис.1).
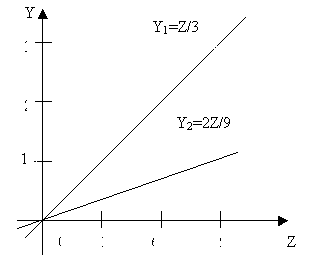
 Рис 1.
Рис 1.
Построенные прямые, называемые кривыми Энгеля, характеризуют покупательский спрос в зависимости от дохода. В данном случае спрос на данный товар возрастает примерно пропорционально доходу, что характерно, например, для спроса на одежду, фрукты и др.
Литература: Красс М.С. Математика в экономике. Основы математики: Учебник.-М.: ИД ФБК-ПРЕСС.2005. с. 360-364. Федосеев В.В., Эриашвили Н.Д. Экономико-математические методы и модели в маркетинге.- М.:ЮНИТИ_ДАНА,2001.с.116-122.
