Д.э.н. Ахметжанов Б.А., к.т.н. Судариков А.Е., Якупова О.В. Карагандинский государственный технический университет, Казахстан

Информационные системы в экономике

Международный финансовый кризис и связанные с ним падение производства и спроса на уголь вынуждают принимать первоочередные меры по снижению трудоемкости и себестоимости добычи угля, повышению качества и выделению средств на развитие шахт и разрезов.

Одним из главных признаков угольного производства является стохастичность процессов и вероятностный характер параметров. Это обстоятельство оказывает существенное влияние на определение условий, параметров характер решаемых задач в области оптимального ведения горных работ.

Во всех случаях качество угля, поступающего на обогащение, зависит от отдельного забоя или шахты. Поэтому, вопрос о том, как в настоящее время учитывается качество угля при планировании развития горных работ на шахте, достаточно рассмотреть на примере какой-либо одной формы организации комплекса.

Исходные качественные характеристики добываемых углей заданы природой и неодинаковы даже в пределах одного шахтного поля. Эффективность горного производства определяется целесообразностью разработки имеющихся запасов месторождений.

Особенностью карагандинских углей является их неоднородный петрографический состав и низкий интервал степени метаморфизма. Качество угля, добываемого в очистных забоях на отдельных шахтах определяется, в зависимости от марочного соотношения (марки К и КЖ), характеристики получаемого концентрата и его выход (%).

Чтобы обеспечить стабильность качественных характеристик перерабатываемого угля, таких как зольность, содержание серы и влаги, необходимо смоделировать и обосновать рациональную модель, которая определит порядок отработки пластов, участков и шахтных полей в целом с заданным качеством.

При разработке предсказывающей модели достаточно эффективным является использование метода множественной регрессии. Опубликовано большое число работ, в которых множественный регрессионный анализ применялся для математического описания различных объектов и явлений [1].

Регрессионный анализ позволяет изучить влияние на исследуемый показатель ряда факторов, имеющих случайный и неслучайный характер, определить вклад каждого из них, влияние в совокупности и в чистом виде, количественно оценить связи между исследуемыми величинами в условиях действия большого числа факторов.

(1)

где bi, - коэффициенты уравнения множественной регрессии;

bо - свободный член уравнения множественной регрессии;

хi – независимые переменные.

Для определения наличия связей между исследуемыми величинами обычно определяют следующие характеристики и критерии, обозначенные через независимые переменные:

х1 - независимая переменная, определяющая процентное содержание угля марки К в общем объеме, поступающем на переработку, %; х2 - независимая переменная определяющая содержание золы в угле марки К, %; хЗ - независимая переменная, определяющая процентное содержание серы в угле марки К, %; х4 - независимая переменная, определяющая содержание влаги в угле марки К, %; х5 - независимая переменная, определяющая процентное содержание марки КЖ в общем объеме угля поступающего на переработку, %; х6 - независимая переменная, определяющая процентное содержание золы в угле марки КЖ, %; х7 - независимая переменная, определяющая процентное содержание серы в угле марки КЖ, %; x8 - независимая переменная, определяющая процентное содержание влаги в угле марки КЖ, %.

(2)

Наиболее часто используемой характеристикой тесноты связи между двумя случайными величинами является коэффициент корреляции (формула 3).

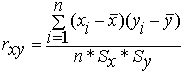(3)

где - средние величины функций и аргументов;

Sx, ,Sy - среднеквадратические значения функций и аргументов;

STATISTICA является наиболее динамично развивающимся статистическим пакетом и по многочисленным рейтингам является мировым лидером на рынке статистического программного обеспечения [3,4].

Она включает в себя мощные возможности по работе с данными, богатые графические возможности и большое количество методов и процедур статистического анализа. STATISTICA 6.0 полностью удовлетворяет основным стандартам среды Windows. Это, прежде всего стандарты пользовательского интерфейса - MDf, использование технологий DDE - динамического обмена данными из других приложений, OLE - связывания и внедрения объектов, поддержка основных операций с буфером обмена и др.

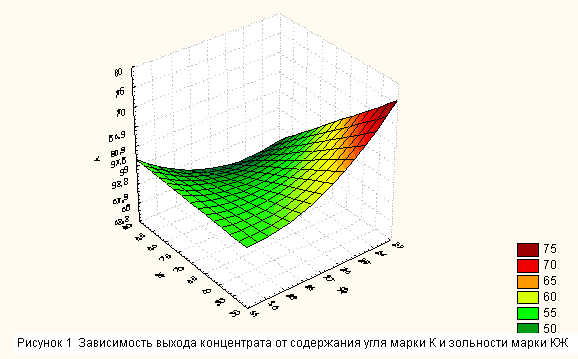
Для более наглядного отображения связей исследуемых параметров, путем аппроксимации в трехмерном пространстве построены графики зависимости выхода концентрата от технологических параметров обогащаемого угля. Изображение в трехмерном пространстве связи исследуемых факторов позволяет визуально определять области, представляющие наибольший интерес для дальнейшего, более глубокого исследования.

На рисунке 1 изображена зависимость выхода концентрата (у) от зольности угля марки К (х2) и зольности угля марки КЖ (х6) в обогащаемой шихте. Анализ рисунка позволяет сделать вывод, что максимальный выход концентрата достигается при зольности угля марки К не более 31,0% и зольности угля марки КЖ не более 26,3%.

Таким образом, в результате реализации модели была найдена теоретическая зависимость выхода концентрата от количественного и качественного состава исходной шихты для обогащения. В результате анализа было установлено, что наибольшее влияние на выход концентрата оказывает процентное соотношение марок угля в исходной шихте, максимальный выход концентрата достигается при коэффициенте марочного состава для угля марки К равном 0,55, для угля марки КЖ соответственно 0,45.

Определенные оптимальные параметры по результатам многомерного корреляционного анализа (х1-х8), позволяют получить минимально возможный выход концентрата равный 56,04% (при среднем выходе концентрата 59,63%). Теоретически максимально возможный выход концентрата может достигать 65,07%. Рациональное соотношение марок и определенное в результате исследования влияние показателей качества исходной шихты на выход продуктов обогащения дают, в свою очередь, возможность значительно рационализировать календарное планирование.

Литература: Дрейпер Н. Смит Г. Прикладной регрессионный анализ. М.: Финансы и статистика.- 1986. Шепелев И. Г. Математические методы планирования и управления в строительстве. Челябинск.: Челябинский политехнический институт.- 1974. Боровиков В. П., Боровиков И. П. Статистический анализ и обработка данных в среде Windows. М.: Информационно-издательский дом “Филинъ”.- 1998. Боровиков В. П. Популярное введение в программу Statistica. М.: Компьютер пресс.- 1998.