Дмитренко И.С.
Донбасская государственная машиностроительная академия
Графоаналитический метод решения задач с нелинейной системой ограничений и целевой функцией
Исходя из уровня знаний, подготовки, и следуя наиболее понятному для студенчества наглядному способу решения задач, было решено практиковать на занятиях по дисциплинам: исследование операций и экономико-математические методы решения задач, графоаналитические методы решения задач нелинейного программирования как наиболее эффективные, наглядные и понятные методы решения.
В данной статье пойдет речь об одной из многих экономических моделей, рассматриваемых в образовательном процессе и о возможном ее решении графоаналитическим методом, синтезирующим графические построения и аналитические расчеты.
Постановка задачи взята из [2]. Предприятие может выпускать два вида изделий. На их изготовление идет два вида ресурсов. Запасы ресурсов на предприятии, плановые нормы их расхода ![]() , плановая себестоимость
, плановая себестоимость ![]() и оптовые цены указаны в таблице (все данные в расчете на 1 тыс. шт. изделий).
и оптовые цены указаны в таблице (все данные в расчете на 1 тыс. шт. изделий).
|
Тип ресурса |
Запас ресурса |
Нормы расхода на одно изделие вида | ||
|
А |
1 |
500 |
20 |
10 |
|
2 |
699 |
30 | ||
|
Себестоимость |
5 |
4 | ||
|
Цена |
9 |
7 | ||
Из-за брака в производстве расход ресурсов зависит от объема ![]() производства и в первом приближении выражается линейной функцией
производства и в первом приближении выражается линейной функцией ![]() , а себестоимость
, а себестоимость ![]() продукции - функцией
продукции - функцией ![]() . Изделия могут выпускаться в любых соотношениях, так как сбыт, обеспечен. Составить план выпуска изделий, обеспечивающий получение максимальной прибыли.
. Изделия могут выпускаться в любых соотношениях, так как сбыт, обеспечен. Составить план выпуска изделий, обеспечивающий получение максимальной прибыли.
Так как ![]() - объем производства изделия вида А,
- объем производства изделия вида А, ![]() - объем производства изделия вида В, то на производство
- объем производства изделия вида В, то на производство ![]() и
и ![]() единиц изделий А и В будет израсходовано
единиц изделий А и В будет израсходовано
![]() единиц ресурса 1-го типа и
единиц ресурса 1-го типа и
![]() единиц ресурса 2-го типа
единиц ресурса 2-го типа
Составим функцию прибыли по формуле: П=Ц-С. Таким образом, полная прибыль от производства ![]() и
и ![]() единиц изделий А и В будет равна:
единиц изделий А и В будет равна:
![]()
Итак, математическая модель задачи имеет вид:
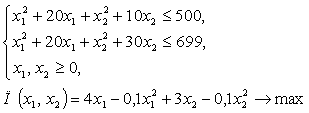
Данная задача относится к задаче нелинейного программирования, т.к. переменные ![]() и
и ![]() входят в ограничения и целевую функцию в степенях выше первой.
входят в ограничения и целевую функцию в степенях выше первой.
В системе ограничений выделим в левой части неравенств полные квадраты, приведем уравнение кривой второго порядка к каноническому виду:
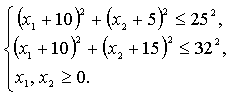
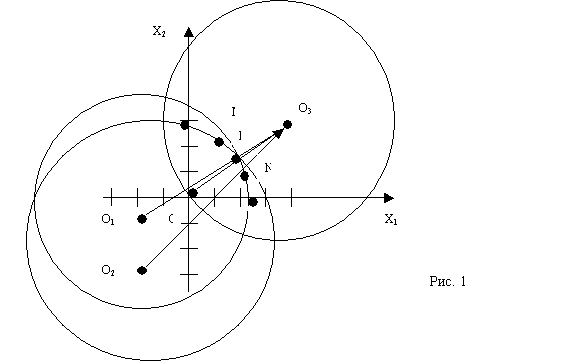
Данные кривые второго порядка представляют собой окружности, с центрами в точках О1(-10;-5) и О2(-10;-15) и радиусами R1=25 и R2=32 соответственно. Построим множество решений задачи – криволинейную область ОАВС (рис 1).
![]() или
или ![]()
Данная кривая – окружность с центром в точке О3(20;15) и радиусом R3=25. Определим направление ( в точке О(0;0)), в котором целевая функция возрастает (т.к. необходимо найти максимум этой функции) – это направление указывает вектор- градиент целевой функции. ![]() . Направление градиента - к центру окружности – точке О3(20;15). Таким образом, точка, в которой целевая функция имеет наибольшее значение будет лежать либо на дуге АВ, либо на дуге ВС, в точке касания линии уровня целевой функции к дуге соответствующей окружности, либо в точке пересечения окружностей- точке В. Координаты точек касания M и N и точки пересечения В, а также значения целевой функции в них можно найти, используя элементарные формулы аналитической геометрии на плоскости. Отметим лишь, что максимум данной функции находится в точке N(12,63;7,63), а значение максимальной прибыли П= 51,63362.
. Направление градиента - к центру окружности – точке О3(20;15). Таким образом, точка, в которой целевая функция имеет наибольшее значение будет лежать либо на дуге АВ, либо на дуге ВС, в точке касания линии уровня целевой функции к дуге соответствующей окружности, либо в точке пересечения окружностей- точке В. Координаты точек касания M и N и точки пересечения В, а также значения целевой функции в них можно найти, используя элементарные формулы аналитической геометрии на плоскости. Отметим лишь, что максимум данной функции находится в точке N(12,63;7,63), а значение максимальной прибыли П= 51,63362.
Таким образом, можно сделать вывод, что данному предприятию, в соответствующих экономических условиях, необходимо выпускать 12,63 тыс.шт. изделий вида А и 7,63 тыс.шт. изделий вида В, максимальная прибыль предприятия при этом составит порядка 51,63362 ден.ед.
Заметим, что решение задач нелинейного программирования графическими методами на практических занятиях по исследованию операций, либо какой-либо другой экономико-математической дисциплине, является лучшей адаптированной схемой к построению наиболее приближенным к современным экономико-математическим моделям промышленности, и довольно не сложным и понятным для нынешнего студенчества методам построения решения. Данные методы используют достаточно большой объем материала аналитической геометрии и дифференциального исчисления для реализации подобных моделей. Тем не менее, следует отметить, что графоаналитический метод решения соответствующих моделей легко программируется и может также использоваться при выполнении курсовых и дипломных проектов для студентов старших курсов.
Литература:
1. Ляшенко И.Н., Карагодова Е.А., Черникова Н.В., Шор Н.З. Линейное и нелинейное программирование. Киев, «Высшая школа», 1975. 348-350с.
2. Сборник задач и упражнений по высшей математике: Мат. программирование: Учеб.пособие / А.В.Кузнецов, В.А.Сакович, Н.И.Холод и др.; 2-е изд.,перераб. и доп.- Мн.:Выш.шк.,2002. 271-278с.
