Керимкулов С.Е., Кантарбаева А.У.

Использование «бегущей средней» для построения регрессионной модели

На этом круглосуточно работающем и являющимся самым ликвидным рынком в мире ежедневно заключаются контракты покупки-продажи валют со сроком от одного дня до 12 месяцев. Основными валютами на этом рынке являются доллар США, евро, японская йена, швейцарский франк, английский фунт стерлингов.

Эконометрические исследования развития экономических показателей в условиях высокой неопределенности и динамичности требуют обобщения и развития современных методов на принципиально новых подходах экономической науки.

Определение и изучение финансового рынка в целом и котировок цен в частности является основной задачей технического анализа финансовых рынков. Методы технического анализа включают в себя методы фильтрации основанных на применении математических формул к движениям рынка. Методы этой группы различными способами подают сигналы о развороте бычьего или медвежьего тренда, а также подтверждают тот или другой сценарий развития цены – рост, спад или отсутствие серьёзных движений (см. [1-3]).

Одним из инструментов методов фильтрации являются скользящие средние. Средние величины предназначены для сглаживания случайных колебаний цены и выявления трендов. Однако, при построении графика скользящей средней существует проблема выбора порядка или «времени пробега» средней подходящего под анализ нужного периода каждого ценового тренда (средняя большого порядка будет постоянно отставать, средняя очень малого порядка будет давать очень много ложных сигналов).

Пусть ,  неравномерные групповые периоды времени , где  --я группа периодов времени с промежутком времени .

Условное математическое ожидание  временного ряда независимых случайных величин ,  на множестве  определяется величиной [1-2]:

,                                           (1)

если ряд (1) сходится, где

-условная вероятность.

Дисперсия  временного ряда независимых случайных величин ,  на множестве  определяется величиной [1-2]:

,                                                (3)

если ряд (1) сходится, где

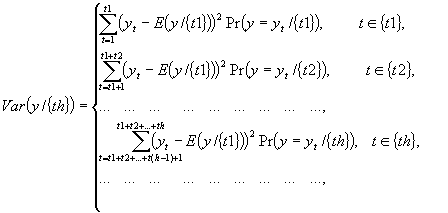, ,        (4)

-условная вероятность.

,                                                (5)

, ,                   (6)

где  неизвестная случайная величина.

Основные предпосылки регрессионной модели [1-2]:

1. Кусочно-постоянные значения параметров  на множестве :

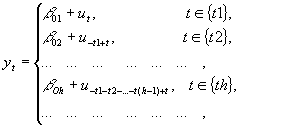                                  (7)

где  случайные ошибки.

2. Временной ряд ,  и случайные ошибки  независимо распределенная выборочная случайная величина.

3. Временной ряд  и ,  и случайные ошибки  и ,  некоррелированы:

; .                              (8)

4. Математическое ожидание случайных ошибок  равно нулю:

.                                                   (9)

5. Временной ряд ,  и случайные ошибки  нормально распределенная случайная величина.

В труде [4] работы Отелбаева подробно изложены известные модели  «усреднения Отелбаева» которые предполагают построение неравномерных групповых периодов времени  временного ряда ,  Отметим, что она использована для асимптотической оценки функции распределения собственных значений дифференциальных операторов.

«Время пробега» -й группы периодов времени с длиной , ,  временного ряда ,  с постоянной дисперсией является величина, соответствующая условию:

, .                                 (10)

Предлагаемый метод предполагает самонастраивание «времени пробега» в зависимости от динамичности рассматриваемого процесса.

Результативность построения средней зависит от того, на сколько точно мы приблизились в построении средних к циклу колебаний курса. Чем точнее угадан цикл, тем точнее выводы. Так как, в случае построения средней со значительным сдвигом от курса можно столкнуться с явлением, когда правила анализа средних не только не помогает, но и даёт прямо противоположные результаты.

Механизм самонастраивания «времени пробега» в зависимости от темпа движения и направления курса позволяет при построении бегущей средней приблизиться к циклу колебаний курса, что является не маловажной задачей при построении регрессионной модели.   

«Бегущей средней» ,  временного ряда ,  с постоянной дисперсией называется величина [4]:

, .                                  (11)

Тогда неравномерные групповые периоды времени  с постоянной дисперсией на -й группы периодов времени с длиной времени  для временного ряда ,  определяется как объединение взаимно-непересекающейся группы периодов времени составленных с промежутком времени «время пробега»  и интервалов , т.е. , где  .

Теперь рассмотрим конкретный пример временного ряда, составленного на основе архивных данных из интернета ресурса, например (см. [5]) ежеминутного торга как цена открытия обменного курса Евро/Доллар США на торговой сессии мирового рынка валют FOREX от 6 января 2009 года за 6 часов (см. Табл. 1 и Рис. 1).

Таблица 1

Цена открытия торговой сессии мирового рынка валют FOREX от 6 января 2009 года за 6 часов, минут, Евро/100Доллар США*

________________________________

*) Интернет ресурс: http://www.forexite.com/free_forex_quotes/forex_history_arhiv.html [5]

Далее используя определения условное математическое ожидание (1), дисперсии (3), спецификации и основные предпосылки регрессионной модели (7)-(8) временного ряда ,  на множестве неравномерных групповых периодов времени , также применяя метод наименьших квадратов, получим оценки параметров регрессии:

                                (12)

числовые значения, которых приведены в таблице 2.

Таблица 2

Расчетная цена торговой сессии мирового рынка валют FOREX от 6 января 2009 года за 6 часов, минут, Евро/100Доллар США*

________________________________

*) Интернет ресурс: http://www.forexite.com/free_forex_quotes/forex_history_arhiv.html [5]

Цена открытия и регрессионная модель торговой сессии мирового рынка валют FOREX от 06.01.2009г. за 6 ч., минут, Евро100/Доллар США100*

Рисунок 1

________________________________

*) Построено авторами на основе: http://www.forexite.com/free_forex_quotes/forex_history_arhiv.html [5]

Построение графика средней осуществляется  способом создания  границ вариации для временного ряда ,

,                                                       (13)

, ,                  (14)

и как следствие создание периода отвечающего условию (11):

,                                          (15)

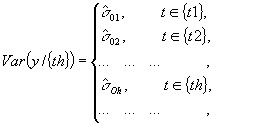, ,                  (16)

каждому временному ряду ,  соответствует дисперсия ,  Увеличение порядка средней не отвечающего условию (11) путём включения в период нового временного ряда приведёт к резкому скачку вариации.

Литература

[1] Greene, William H. Econometric analysis. 6th edition. New Jersey: Prentice Hall, - 2008. – 1178p.

[2] Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера.– М.: ЮНИТИ-ДАНА, 2002.-311с.

[3] Керимкулов С.Е. Моделирование макроэкономических процессов в Казахстане. Монография. Алматы: НИЦ «Fылым», – 2001.-240 с.

[4] Отелбаев М. Оценки спектра оператора Штурма-Лиувилля, Алма-Ата, «Ғылым», 1990.

[5] Котировка торговой сессии мирового рынка валют FOREX от 6 января 2009 года / Архив котировок торга FOREX / Интернет ресурс: http://www.forexite.com/free_forex_quotes/forex_history_arhiv.html