Кучеренко А.Г.

Обучение нейронной сети с использованием алгоритма сопряженных градиентов и множественной линейной регрессии для задачи прогнозирования спроса

Цель работы – моделирование динамики продаж продукции с применением нейронных сетей для предсказания объема спроса в будущем периоде.

Чаще всего для прогнозирования применяются нейронные сети, обучаемые по алгоритму обратного распространения ошибки. Классическое обратное распространение – алгоритм градиентного спуска первого порядка, в соответствии с которым корректируются весовые коэффициенты сети в направлении антиградиента. Он обладает некоторыми недостатками, такими как линейная сходимость и попадание в зону локального минимума. Для преодоления этих сложностей алгоритм подвергают различным модификациям: расчетом градиента на основе матрицы производных второго порядка, применения алгоритмов нечеткой логики, имитации отжига.

Обучение нейронной сети представляет собой многокритериальную задачу нелинейной оптимизации. Её целью является поиск оптимального набора весовых коэффициентов (экстремума функции) для минимизации ошибки сети.

В данной работе рассматривается применение алгоритма сопряженных градиентов, имеющим большую эффективность по сравнению с классическим алгоритмом наискорейшего спуска, и метода множественной линейной регрессии для неслучайной инициализации весовых коэффициентов.

В задаче обучение нейронной сети алгоритм сопряженных градиентов применяется для минимизации квадратичной функции вида

                                        ,                                        (1)

где w – вектор n элементов; G – матрица Гессиана.

Направление поиска экстремума выбирается таким образом, чтобы оно было ортогональным и сопряженным со всеми предыдущими направлениями:

где  – фактическое значение направления градиента.

Изменение весов рассчитывается по формуле

                                              .                                              (3)

Коэффициенты  и  используются для определения сопряженного направления. Значение  должно минимизировать , для расчета можно применить метод золотого сечения или другой линейный алгоритм поиска минимума. Для расчета коэффициента  применяется формула Флетчера–Ривза:

                                                .                                                (4)

Для квадратичных функций метод сопряженных градиентов находит минимум за n шагов (n – размерность пространства поиска), поэтому алгоритм нуждается в перезапуске на каждом  шаге. Для метода Флетчера–Ривза это выполняется с помощью .

1. Инициализация весов  ().

2. Расчет градиента .

3. Определение направления .

4. Расчет .

5. Коррекция весовых коэффициентов .

6. Если ошибка несущественна – остановить обучение.

7. Если  установить ,  и перейти к шагу 2.

8. Определить .

9. Рассчитать , , вектор направления  и перейти к шагу 4.

Для расчета градиента на этапах 2 и 9 используется целевая функция ошибки нейронной сети:

                                      .                                      (5)

где N – количество обучающих образов;  и  – фактический и желаемый выходы сети соответственно.

Выбор стартовой точки, который обеспечивается первоначальной инициализацией весов сети, играет важную роль в процессе обучения.

Инициализация случайными равномерно распределенными значениями, харак­терная для градиентных алгоритмов, не гарантирует избегания локальных минимумов в процессе спуска. Этот этап может быть преодолен с применением множественной линейной регрессии (МЛР). В этом случае весовые коэффициенты связей входного и скрытого слоев по-прежнему инициализируются случайно, а веса связей скрытого и выходного слоев рассчитываются с помощью МЛР.

Процедура неслучайной инициализации выглядит следующим образом.

Как только инициализированы веса нейронов скрытого слоя и на вход сети подан обучающий образ, рассчитывается сигнал перед выходным слоем:

                                               ,                                               (6)

где s – номер обучающего образа; i – номер нейрона входящего слоя; j – номер нейрона скрытого слоя;  – вес связи нейронов между входящим и скрытым слоями;  f – функция активации.

Выходной сигнал сети рассчитывается по формуле:

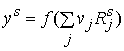                                               ,                                                (7)

где  – вес связи между скрытым и выходным слоями.

Сигмоидальная функция активации 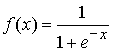 разлагается в ряд Тейлора:

                                                 .                                                  (8)

Применяя линейную аппроксимацию (8) к (7) получаем линейную связь между выходами сети и сигналом скрытого слоя:

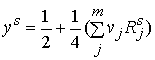                                                                                          (9)

или

                                  ,                                  (9)

где m – количество нейронов в скрытом слое.

Уравнение (9) является типичной моделью множественной линейной регрессии, где  – независимая переменная, а параметр  оценивается стандартными регрессионными методами.

Для проведения эксперимента использовались данные некоторой коммерческой фирмы о продажах изоляционных материалов и проведении маркетинговых акций (участии в выставках). Структура выбранных данных представлена в таблице 1.

Таблица 1 – Структура данных

Использование атрибута Месяц года обусловлено необходимостью передать нейронной сети информацию о сезонности прогнозируемой величины. Участие в выставке характеризует возможный всплеск величины продаж в будущих периодах. Каждый тренировочный образ содержит значения выбранных атрибутов за 5 последних недель.  Прогнозируемая величина характеризует объем спроса в будущем периоде. Соответственно, сеть имеет 15 нейронов во входном слое и 1 нейрон на выходе. В скрытом слое решено разместить 9 нейронов. Обучающая выборка содержит 200 образов, еще 50 образов составили контрольную выборку и в процессе обучения не предъявлялись сети.

Прогнозирование проводилось по четырем сценариям:

1. Использование алгоритма сопряженных градиентов с МЛР;

2. Использование алгоритма сопряженных градиентов без МЛР.

3. Использование алгоритма наискорейшего спуска с МЛР;

4. Использование алгоритма наискорейшего спуска без МЛР.

Производительность сценариев оценивалась по таким показателям: количеству итераций алгоритма, СКО и проценту правильно предсказанных знаков изменения.

Результаты представлены в таблице 2.

Эксперимент показал, что прогнозирование объемов спроса с использованием исторических данных, учетом сезонной компоненты и временем проведения маркетинговых мероприятий возможно с удовлетворительным уровнем ошибки.

Талица 2 – Результаты эксперимента

Также эксперимент подтвердил, что алгоритм сопряженных градиентов позволяет обучить сеть быстрее наискорейшего спуска.

Неслучайная инициализация весов нейронов выходного слоя существенно повлияла на производительность алгоритмов, позволив в случае с алгоритмом сопряженных градиентов в полтора раза сократить количество итераций. Дальнейшее увеличение эффективности может быть достигнуто с применением методов инициализации весов связей между нейронами входного и скрытого слоев. Это может быть реализовано с помощью алгоритмов нечеткой логики, имитации отжига и др. Другим путем повышения эффективности является использование более сложных сетевых архитектур.

Литература:

1. В.В. Круглов, В.В. Борисов. Искусственные нейронные сети. Теория и практика. 2 изд. – М.: Горячая линия – Телеком, 2002. 382 с.

2. С. Оссовский. Нейронные сети для обработки информации. – М.: Финансы и статистика, 2002. 344 с.

3. О.Г. Руденко, Е.В. Бодянский. Искусственные нейронные сети: Научное пособие. – Харьков: ООО «Компания СМИТ», 2006. 404 с.