Броншпак Г.К, Бубенко П.Т., Чернышов С.И.

Математические аспекты обоснования эффективности экономического кластера

В настоящее время экономическая наука активно использует математический аппарат, включая его достаточно сложные разделы. К ним, в частности, можно отнести теории множеств, игр и катастроф. Вместе с тем, поведение экономических систем, в первую очередь, определяют процессы генерации и распределения материально-финансовых ресурсов между субъектами хозяйственной деятельности, что позволяет выстраивать балансовые соотношения. Они органично сопрягаются с аппаратом линейной алгебры, который предоставляет эффективные средства, как аналитического исследования, так и численной реализации.

В этой связи модель Леонтьева «затраты – выпуск» широко применяется для анализа макроэкономических процессов. Однако заметим, с математической точки зрения, являются упомянутые выше субъекты отраслями, или же предприятиями не имеет значения и, тем не менее, авторам не встречались содержательные примеры реализации данной модели в задачах микроэкономического уровня.

Причина, в определенной мере, объясняется отсутствием статистических данных, которые необходимы для построения матрицы баланса. Действительно, предприятие располагает информацией лишь по вопросам непосредственного взаимодействия с партнерами, но о том, как они могут быть связаны между собой, практически ничего не знает. Кроме того, трудно указать критерий, на основании которого устанавливались бы границы такого баланса. То есть, скольких субъектов и по какому принципу следует учитывать?

В противовес сказанному, макроэкономические балансы могут привязываться, например, к количеству отраслей; существуют службы, которые занимаются сбором и обработкой статистической информации. Однако такой процесс является достаточно продолжительным и соответственно использование результатов исследования балансовых соотношений для управления экономикой в режиме реального времени становится невозможным.

На основании приведенных соображений, нами сделан вывод, который представляется существенным. Его смысл состоит в том, что модель Леонтьева в стоимостной интерпретации очень органично сопрягается с кластером и может быть эффективно использована для принятия решений по управлению его текущей деятельностью. При этом под управлением мы понимаем координацию действий участников кластера. Такая область практических приложений модели «затраты – выпуск» с новой стороны раскрывает ее замечательный потенциал.

Определяющую роль в этой связи играют следующие факторы:

- процедура такой идентификации представляет собой один из важнейших инструментов кластерной теории;

- обмен информацией между участниками кластера о перетекании материально-финансовых потоков позволяет оперативно определять элементы упомянутой матрицы;

- подобного рода информационный обмен олицетворяет собой ключевую особенность кластера как организационно-экономической системы.

Заметим также, что в ходе практической реализации координационных мероприятий объективно присущее кластеру качество взаимного доверия между участниками позволяет замыкать встречные потоки посредством сглаживания временных лагов, без чего соотношения баланса потеряли бы смысл. Иначе говоря, если баланс строится сегодня, отгрузка товара произошла вчера, а оплата поступит завтра, то сдвиги по времени нивелируются.

И, наконец, немаловажная деталь состоит в том, что высокая степень открытости коммерческой информации препятствует получению участниками кластера теневых доходов. Действительно, если элементы матрицы баланса – фиктивны, то решения, принимаемые с ее помощью, окажутся ошибочными, а соответственно проблема конкурентоспособности такого «кластера» переходит в иррациональную плоскость.

Собственно говоря, и понятие кластера как организационно-экономической системы, участники которой на неформальной основе обмениваются знаниями и опытом, утрачивает в этом случае предметный смысл. Нельзя ли предположить, что именно вследствие фактора детенезации доходов – ВТО так благоприятствует развитию кластеров, в противовес субсидированию национальных производителей государством по отраслевому признаку?

Содержащийся далее материал посвящен вопросам реализации модели Леонтьева под углом зрения преимуществ в этой связи кластерной организации. В процессе изложения будут показаны аналитические возможности аппарата линейной алгебры применительно к классу матриц, которые характерны для данной модели (п.1). Мы заострим внимание на интерпретации с помощью соотношений баланса неустойчивых состояний экономической системы, когда ее поведение может непредсказуемо преобразиться под воздействием малых возмущений (п.2).

В конструктивном отношении, заслуживает внимания раскрытие уникальности потенциала кластера по обеспечению своей конкурентоспособности, а также особенность его функционирования на условиях внутренних цен (п.3). Приведенные здесь доводы базируются на методологии рационального сочетания расчетно-теоретических возможностей с механизмами принятия решений гуманитарного свойства, которые объективно присущи кластеру.

Общие соображения и выводы концептуального характера подытоживает ряд конкретных примеров (п.4). Они наглядно демонстрируют, как явления структурной неэффективности экономической системы, так и возможность их преодоления с помощью кластерного подхода.

1. Методологический потенциал соотношений стоимостного баланса

Использование балансовых соотношений позволяет свести определение стоимостей продукции участников производственно-коммерческого процесса к решению системы линейных алгебраических уравнений , где векторы

, или

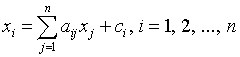.                                                                          (1)

Здесь  – стоимость продукции -го участника (при неизменных объемах производства или услуг аналогичная цене);  – часть стоимости продукции -го участника, составляющая его доход;  – часть стоимости продукции -го участника, которую потребил -й участник;  – вклад -го участника в производство -го вида продукции (включая оплату труда, материалов, услуг сторонних организаций и т. п.), а также часть оплаты -го внешнего потребителя, приходящаяся на компенсацию себестоимости производства -го вида продукции.

При этом  и  предполагаются данными. Вследствие сделанных определений  (что означает неотрицательность матрицы ); . Случай  соответствует посреднической, франчайзинговой деятельности, а также использованию прошлого опыта, знаний и т. п. Заметим, что модель (1) непосредственно распространяется на ситуацию, когда участники производят по нескольку видов продукции.

Как представляется, в задачах микроэкономики «стоимостная» модель имеет существенные преимущества по сравнению с трактовкой  и  как натуральных величин (см., например [1, с. 11-12]). Действительно, у всех  в (1) – одинаковая размерность – денежного эквивалента. Соответственно весьма прозрачен предметный смысл безразмерных коэффициентов . И, напротив, дробного вида размерность  в «натуральной» модели существенно осложняет использование аппарата матричного анализа для исследования и численной реализации системы уравнений (1).

Заметим также, что, как правило, соотношения между объемами продукции участников микроэкономической системы, необходимые для того, чтобы обеспечить нужный уровень и структуру конечного выпуска, можно определить из соображений технологического характера. В условиях конкурентной среды гораздо более информативны показатели стоимости этой продукции, поскольку от них непосредственно зависят как персонификация потенциальных партнеров, так и спрос внешнего потребителя.

По теореме Хоукинса – Саймона для строгой положительности решения системы уравнений (1), при сделанных выше предпосылках, необходимо и достаточно, чтобы все главные миноры , где

– единичная матрица, были положительными [1, с. 29]. Практический смысл решения  очевиден, поскольку стоимость видов продукции (услуг) не может равняться нулю или быть отрицательной.

Методы вычисления определителей хорошо известны [2, с. 165-168; 3, с. 191-196], однако даже при сравнительно небольшом порядке  они не являются конструктивными. Причина заключается в быстром накоплении погрешности округления значащих цифр (см., в частности, замечание В.В.Воеводина [4, с. 7]). Поэтому с уверенностью судить об удовлетворении конкретной матрицы  условиям данной теоремы не представляется возможным. Следует также заметить, что предметная интерпретация упомянутых миноров весьма затруднительна.

Р.Беллман, исключая эти условия, потребовал строгой положительности всех  и соответственно

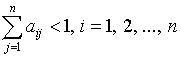  [5, с.329-331]. Однако такой подход не всегда приемлем из-за сужения класса рассматриваемых задач. Действительно, получается, что каждый из участников экономической системы (1), должен обязательно вносить в выпускаемую им продукцию свой труд текущего периода. Для организаций кластерного типа, где развиты отношения неформального партнерства, подобного рода ситуации, в целом, не характерны.

Предусмотрен также случай , но при этом все  должны быть строго положительны, что редко встречается в экономике. Действительно, все участники экономической системы должны непосредственно взаимодействовать друг с другом.

В этой связи большой интерес представляет замечание М.Моришима, со ссылкой на Р.М.Солоу, о том, что для удовлетворения условиям Хоукинса – Саймона матрица  должна быть неразложимой [1, с. 29]. То есть такой, что перестановкой строк и столбцов ее нельзя привести к виду

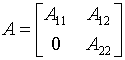, где на главной диагонали располагаются квадратные матрицы. Одновременно предполагается, что суммы элементов каждой из строк матрицы  не превышают единицу и хотя бы одна из этих сумм меньше единицы. Данная предпосылка полностью соответствует сказанному выше в отношении системы уравнений (1).

Критерий Солоу базируется на теоремах Перрона-Фробениуса, которые в весьма отчетливой форме представлены М.Моришима [1, с. 247-248] и являются исключительно важными для практических приложений. Они позволяют судить о рациональности структурного устройства экономической системы на основании свойств соответствующей матрицы . В первую очередь, можно сделать вывод о том, что неразложимость матрицы  представляет собой весьма существенную предпосылку эффективного функционирования экономической системы.

Действительно, если матрица  неотрицательна, неразложима,

(одна из сумм строго меньше единицы), то , матрица, обратная , положительна и решение системы уравнений (1) определяется как

.                                                                                             (2)

Если та же матрица  разложима, то гарантируется лишь . Утверждения теорем Перрона-Фробениуса допускают целый ряд интерпретаций в категориях предметной области. Так, если матрица  разложима, то экономическая система, описываемая системой уравнений (1):

- может плохо поддаваться управлению, о чем свидетельствует неадекватность реагирования ее неотрицательного собственного значения  (см. ниже (3)) на изменение элементов ;

- по той же причине, отдельные подсистемы могут быть неудовлетворительно сопряжены между собой и, вообще, обладают способностью производить ненужную работу, расходуя ресурсы;

- она также в гораздо большей мере предрасположена к выходу на неустойчивые режимы функционирования, вследствие того что  (отличие от (2) принципиально).

Доказательства теорем Перрона-Фробениуса базируются на исследовании поведения собственных значений матрицы . То есть, параметра , при котором решение однородного уравнения

                                                                                                        (3)

нетривиально. В качестве признания научной значимости полученных результатов, М.Маркус и Х.Минк охарактеризовали свойства неотрицательных матриц как замечательные [6, с. 165] (здесь приведен также большой перечень следствий данных теорем, с. 168-174).

Заметим, что некоторые  значений , удовлетворяющие системе уравнений (1), будучи положительными, тем не менее, могут оказаться ниже себестоимости производства. Если их установить на договорной основе, то определение оставшихся  сводится к решению системы, состоящей из  уравнений:

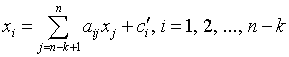, (4) где свободные члены

.

Если при этом все  (что, вообще говоря, является менее вероятным), то решение системы уравнений (4), положительно. В альтернативном варианте (то есть, когда хотя бы одно из значений ): с одной стороны, положительность решения системы уравнений (4) не гарантируется; с другой, постановка задачи во многом утрачивает смысл. Вместе с тем, и негативный результат может быть полезным, сигнализируя о необходимости структурного видоизменения экономической системы.

М.Моришима привел в форме теорем следующие результаты для неразложимой матрицы . Пусть в условиях неизменных объемов выпуска, внешний потребитель готов приобретать продукцию -го участника по более высокой цене, а остальные цены остались прежними. Тогда стоимость продукции всех участников системы (1) возрастет, причем в процентном отношении рост у -го вида продукции будет наибольшим [1, с. 32]. Продемонстрирована также устойчивость динамической системы вида (1) к возмущениям начального состояния, обусловленная  при  [1, с. 37].

Следует принять во внимание, что понятие разложимости неотрицательной матрицы, не связано с ее размером , а зависит лишь от расположения нулевых и ненулевых элементов [7, с. 256]. Это соображение используется при построении, ориентированного графа (орграфа), который соответствует матрице . Орграф матрицы  сильно связен, если для любых двух вершин (подразумеваются участники экономической системы) существует связывающий их ориентированный путь.

Имеется простая проверка, а именно: матрица  неразложима, если ее орграф сильно связен [8, с. 129-130]. Методы поиска сильно связных компонентов больших систем, которые могут быть использованы, в частности, для идентификации потенциальных участников экономического кластера, подытожены С.Писсанецки [9, п.5].

Однако, даже без положений математических теорем, соотношения стоимостного баланса (1) обладают очевидной полезностью. Действительно, посредством вариации значений  и , можно производить целый ряд исследований. Таких как оценка изменения экономической ситуации при необходимости снижения цены вида продукции, или же увеличения объема поставок одному из внешних потребителей и т. п.

Несомненно, подобного рода информация весьма существенна для анализа процессов, происходящих в экономической системе. Важную роль при проведении вариативных расчетов играет детально разработанный аппарат численной реализации систем линейных алгебраических уравнений [2 – 4, 8].

Следует отметить, что материально-финансовые потоки экономических систем в реальной ситуации, как правило, не удовлетворяют условию сильной связности. Для его выполнения необходима слишком высокая плотность непосредственных взаимодействий в каждой из пар участников. Однако здесь вновь обращает на себя внимание кластер. Суть в том, что ему объективно присущ интенсивный обмен между участниками опытом и знаниями (см. основополагающие труды М.Портера и целый ряд других источников [10, 11]).

Передаваясь на безвозмездной основе, они, тем не менее, представляют собой интеллектуальные продукты, которые могут оцениваться в денежном эквиваленте (см., в частности [12, 13]). Вместе с тем, конкретно использовать эти оценки в настоящем не предполагается. Важен собственно факт существования, образно выражаясь, гипотетически неразложимой матрицы интеллектуально-финансовых потоков кластера. Соображения этой направленности будут развиты ниже, п.3.

Сделаем отступление от текста, обратив внимание на используемое нами понятие участника экономической системы (которое ни в коей мере не является оригинальным), хотя можно было бы оперировать, например, с субъектом хозяйственной деятельности. Причина, очевидно, связана с глубоко проникшей в экономику терминологией системного анализа и теории игр. Они, в свою очередь, позаимствовали соответствующие термины из сферы игорных развлечений.

Однако если говорить по существу, то между экономикой, а также, например, искусством дипломатии, ведения войн и т. п., на самом деле, имеется с игрой много общего. Везде существуют свои правила, вынужденно придерживаясь которых, каждый из участников стремится к выигрышу.

Причем, если в карточной игре – четыре участника, то двое из них не имеют права согласовывать свои ходы, или же состоять в сговоре. Правила экономики также запрещают участникам раскрывать друг другу «карты», но только лишь на уровне монополий. Поэтому кластер вполне можно рассматривать в разрезе сговора его участников для совместного противостояния угрозам внешнего окружения. И точно также как в карточной игре они получают, тем самым, весомые преимущества.

Таким образом, с организационно-экономической точки зрения, достоинства кластера несомненны. Включая его полезность для государства, вследствие упоминавшейся выше детенезации доходов, а также перспектив поддержки со стороны международных организаций, развития инфраструктуры региона и т. п. И, вместе с тем, как показывает мировой опыт, создать кластер совсем не просто. В первую очередь, он предъявляет высокие требования к морально-этической состоятельности потенциальных участников, что подразумевает такие качества как готовность к диалогу, принятию компромиссных решений, видению на перспективу и, вообще, отсутствие инстинктов первобытного человека.

Возвращаясь к основной теме настоящего изложения, отметим, что одним из главных преимуществ экономического кластера, по общему мнению, является высокий потенциал достижения синергетического эффекта [14], который зачастую характеризуют как 2 + 2 = 5. Вместе с тем, для его реализации, используя свою координационно-управленческую адаптивность, кластер может временно находиться и в альтернативном состоянии, а именно: 2 + 2 = 3.

Естественно, совершая такого рода «зигзаги», кластер будет вынужден периодически выходить за пределы предпосылок и условий экономико-математических теорем. Так, отвечающая ему матрица  совсем не обязательно будет неотрицательной. Соответственно возрастает роль ситуативного принятия управленческих решений в трудно прогнозируемой ситуации и с этой точки зрения необходимо учитывать следующие обстоятельства.

2. Устойчивость финансовых потоков в контексте обусловленности соответствующих им матриц

Решение системы линейных алгебраических уравнений общего вида

,                                                                                                               (5)

где  – невырожденная матрица, даже в случае невысокого порядка  может обладать неустойчивостью, которая подразумевает неадекватно сильную зависимость решения от элементов матрицы или свободного члена. В подавляющем большинстве случаев это свидетельствует о негативных свойствах рассматриваемой системы.

Число обусловленности матрицы

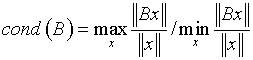, где , играет роль множителя в увеличении погрешности, или же вариации свободного члена  [15, с. 56-58]. Оно является также мерой близости  к вырожденной матрице, хотя точная формулировка данного утверждения проблематична.

Если  невелико, матрица  – хорошо обусловлена, и наоборот. Значение  – гораздо более важный показатель сложности решения системы уравнений (5), чем малая величина  или большой порядок . Очевидно упомянутая сложность непосредственно взаимосвязана со спектром потенциально возможных поведений экономической системы, а соответственно и ее управляемостью. Заметим, что с несколько иных позиций та же проблематика обусловленности матриц освещена в работах [2, с. 145-155; 16, с. 402-411].

В качестве иллюстрации, авторы [15] привели пример:

и, если вектор  заменить близким к нему , то решением становится . При этом

.

Таким образом, при очень малом изменении свободного члена решение совершенно преобразилось. Иначе говоря, для покрытия минимально возросшего спроса в экономической системе должны произойти кардинальные изменения. В категориях экономики ситуацию можно интерпретировать также как прорывный выход более дешевой продукции на монополизированный рынок.

В [3, с. 48-49] рассмотрены две системы уравнений, у которых близки как свободные члены, так и элементы матрицы :

                                                         (6) а решения имеют вид соответственно:

, то есть, резко отличаются. Изменение пятой значащей цифры в компоненте вектора  привело к изменению первой значащей цифры в решении. Причем не существует численного метода, который мог бы устранить такую чувствительность к малым возмущениям.

Модель (6) допускает интерпретацию. Два участника непрочной коалиции выпускают одинаковый вид продукции. Доля второго на рынке немного выше и, тем не менее, выручка делится пополам. Увеличение спроса при сохранении цены продукции приводит к тому, что один участник дважды повторяет хорошо освоенную им процедуру, тогда как другой вынужден покинуть рынок. Соответственно коалиция прекращает существование.

Для несимметричных матриц

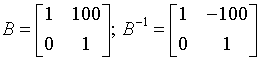 (7) при  решения уравнений  и  имеют вид соответственно: . Таким образом, погрешность порядка 1% в векторе  привела к совершенно неадекватному изменению . Плохая обусловленность в данном случае вызвана тем, что внедиагональные элементы матриц как , так и  одинаково велики. Как отметил Г.Стренг, это противоречит интуитивному представлению о том, что с возрастанием  матрица  должна становиться «меньше» [3, с. 327].

Интерпретировать (7) в качестве экономической модели можно следующим образом. Дешевый продукт с низкой эластичностью исчез. Соответственно замещающий его продукт приобретается по сверхвысокой цене.

Процедура вычисления , где

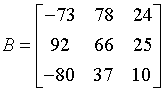                                                                                          (8)

проанализирована в [17, с. 12-13]. Плохая обусловленность такой задачи вытекает из следующего обстоятельства. Пусть

,

тогда , однако, на самом деле . Иначе говоря, если накопление ошибок округления будет соответствовать малому возмущению матрицей , то результаты вычислений окажутся совершенно бесполезными.

Пример показывает, что возмущение минимальной интенсивности одного из звеньев может радикально изменить поведение экономической системы. Однако если о ней судить по величине , иначе говоря, без специального анализа, а в категориях, которые близки к соображениям здравого смысла, то может быть сделан неправильный вывод о неплохой сбалансированности системы (8).

Весьма оригинальный пример для матрицы

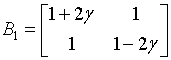,                                                                                        (9) где ,  – единичная ошибка округления в компьютерной памяти, продемонстрировал Б.Парлетт [18, с. 49-50]. Оказывается, если к матрице  прибавить матрицу , то ее наименьшее собственное значение  изменится с  на . Причем, ни один метод не способен вычислить  точнее без повышения разрядности. Малое изменение любого из элементов матрицы (9) в гораздо большей степени сказывается на величине .

В предметном отношении сказанное означает, что экономическая система, имеющая неэффективные связи между участниками, способна легко выходить из равновесного состояния при воздействиях даже слабой интенсивности. Соответственно она является также и плохо управляемой. Наряду с этим матрица

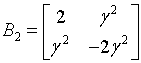имеет приблизительно такой же спектр собственных значений как . Если к  прибавить ту же матрицу , то в элемент  вносится очень большая относительная ошибка. И, тем не менее, она в точности соответствует той ошибке, с которой находится .

Иначе говоря, малые возмущения элементов  адекватно сказываются на решении. Как отметил Б.Парлетт, причина состоит в том, что  представляет собой «крайний» пример специального класса матриц, называемых градуированными. «Меньшие элементы таких матриц располагаются выше больших», например [18, с. 50, 179]:

;

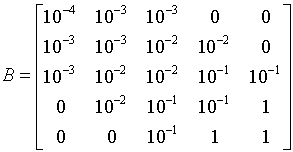(разница численных значений косвенно свидетельствует о потенциале соответствующих алгоритмов численной реализации).

Более точно градуированные матрицы можно определить следующим образом:

- элементы, располагающиеся на главной диагонали, убывают снизу вверх;

- элементы каждого из столбцов, начиная с первого ненулевого значения, убывают снизу вверх;

- при этом элементы, располагающиеся на главной диагонали, представляют собой исключение.

Вследствие таких особенностей появляется вполне реальная возможность для сопряжения связей разной интенсивности и, вообще, целенаправленного создания структурно эффективных систем, что является важным в плане практических приложений. Действительно, предположим, что предметный смысл элементов  матрицы

такой же, как у коэффициентов  системы уравнений (1).

Тогда  можно рассматривать как разность между стоимостью -го вида продукции и вкладом в ее производство -го участника. При  также и все свободные члены . На основании структурного устройства приведенных матриц, можно сформулировать правила построения эффективной системы:

- деятельность всех участников экономической системы – рентабельна, чему соответствуют ;

- рентабельность участников пропорциональна их вкладу в результаты деятельности экономической системы;

- этот вклад определяется значениями ,  и возрастает с увеличением номера строки ;

- наиболее и наименее результативные участники непосредственно взаимодействуют между собой ;

- эта тенденция распространяется в соответствии со снижением (уменьшение ) /повышением (увеличение ) результативности участников;

- часть стоимости продукции -го участника, передаваемой партнеру, увеличивается пропорционально росту его сравнительной результативности (значения).

Заметим, что такого рода интерпретацию нельзя содержательно распространить на случай , где  – матрица системы уравнений (1). Градуированная матрица  и неразложимая матрица , в условиях теоремы Перрона – Фробениуса, могут рассматриваться как олицетворяющие собой различные подходы к достижению структурной устойчивости.

В системе, которую характеризует градуированная матрица , стимулируются: результативность деятельности участников; их концентрация на развитии производственно-коммерческих контактов между собой; содействие процессам системной консолидации. Конечно, в полной мере соответствовать разрешению таких задач может только организация кластерного типа. С этой точки зрения, формирование кластера в привязке к особенностям градуированной матрицы заслуживает серьезного внимания.

Следует подчеркнуть, что, конструктивные рекомендации в отношении, как структуры кластера, так и функций его участников, которые сообщает градуированная матрица, совсем не очевидны. Здесь видится определенная сопряженность с исследованием на основе строгих постановок теории игр Э.Муленом  вопросов мотивации к кооперационной деятельности [19, п.1.2]. По его мнению, кооперация – хрупкое предприятие. Его устойчивость обеспечивают достаточные доходы и справедливость их распределения.

Фактор такой «справедливости» особенно актуален в связи с тем, что для экономических систем характерны матрицы несимметричного вида, с . Задачи на собственные значения для них значительно сложнее, чем в случае  из-за неустойчивости вычислительных процедур. Другая особенность несимметричных задач, существенно затрудняющая их исследование, заключается в том, что собственные числа могут быть комплексными. Поэтому «геометрия» возмущений собственных чисел в несимметричных задачах становится двумерной [20; 21, п.4].

Параметр  является собственным значением несимметричной матрицы  при выполнении неравенства

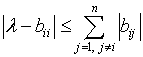 (10) для хотя бы одного значения  [4, с. 63]. Иначе говоря, любое собственное значение матрицы  находится, по крайней мере, в одном из кругов (носящих имя Гершгорина) с центрами . Собственные значения несимметричных матриц, которые заключены в областях пересечений кругов, не удается определять по отдельности.

Поведение экономической системы в такой ситуации оказывается трудно предсказуемым. Можно ожидать наступления критического состояния при, казалось бы, незначительной вариации элементов матрицы . Соответственно система уравнений (5) становится, по существу, неразрешимой, что подразумевает экономический коллапс из-за невозможности проведения товарно-денежных операций. Потенциально опасными в смысле его возникновения могут быть целые диапазоны соотношений между элементами . Вместе с тем, следует подчеркнуть, что для оценки соответствующих областей развит достаточно конструктивный инструментарий на базе критерия (10).

Однако все предшествовавшие рассуждения основывались на предпосылке о том, что матрица  известна. Но такая возможность может быть реализована лишь в формате экономической системы уникального типа, которую мы отождествляем с понятием «кластер». Как представляется, его стратегия должна состоять в том, чтобы максимально соответствовать модели Леонтьева в условиях теоремы Перрона-Фробениуса для неразложимой матрицы (ей  ни чем не угрожает). В ситуациях, когда это становится невозможным, следует, тем не менее, все равно использовать базовую модель, проецируя на нее реалии состояния кластера. С целью предметной интерпретации возникающих отклонений и соответствующей корректировки управленческих решений.

Заметим в этой связи, что при конструировании систем для различных практических приложений, во избежание экстремальных режимов функционирования, обычно стараются сместить параметр  подальше от собственных значений соответствующих матриц. В преломлении к кластеру это может делаться, например, путем распараллеливания материально-финансовых потоков с созданием торгового дома, холдинга, или же неприбыльной организации. Для вычислительного моделирования такого рода мероприятий эффективны алгоритмы, изложенные в работах С.Писсанецки и В.А.Фильштинского [9, 22].

3. Уникальность кластера, как организационно-экономической системы, с позиций матричного анализа

В силу своей сущности конкурентоспособный кластер – это эффективно управляемая организационно-экономическая система. Такую эффективность предопределяет, в первую очередь, интеллектуальный потенциал кластера, включая механизмы координации действий его участников. Очевидно, интеллектуально-информационные потоки кластера имеют высокую степень разветвленности, орграф соответствующей им матрицы  сильно связен и, следовательно, она неразложима (см. п.1).

В противном случае матрицу  легко развить до неразложимой посредством информационной компоненты. Обратим внимание, с такого рода построениями может быть связан один из инструментов конструирования кластера, представляющийся весьма практичным. Иначе говоря, топологические характеристики системы могут использоваться для установления взаимодействий между участниками и выбора траекторий принятия решений.

Совсем иного характера матрица  – материально-финансовых потоков, которая в реальной ситуации, как правило, разложима, вследствие сравнительно небольшой частоты парных взаимодействий. Какую-либо корректировку такого положения ограничивает производственно-технологический фактор. Тем не менее, как матрица , так и

  – квадратные; их элементы являются безразмерными.

Поскольку соответствующие матрице  потоки допускают измерение в денежном эквиваленте (см. п.1), мы можем формально представить общую матрицу финансовых потоков

, (11) где

,

которая, также как и , неразложима. Задача сводится к решению системы линейных алгебраических уравнений

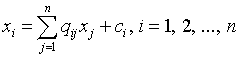.                                                                         (12)

Упомянутая выше формальность обусловливается тем, что процедуры вычисления элементов  достаточно нетривиальны и, в целом, плохо сопрягаются с вопросами ситуативного управления деятельностью кластера. Заметим также, что одна из особенностей нематериального актива, состоит в возможности его многократной передачи без потерь стоимости (в некотором смысле, это противоречит идее баланса).

Однако в настоящем нам важна собственно неразложимость матрицы . При этом для удовлетворения условиям теоремы Перрона-Фробениуса, в интерпретации п.1, требуется чтобы

,                                                                    (13)

причем хотя бы одна из этих сумм была строго меньше единицы. Тогда ,  не является корнем однородного уравнения (3) (при подстановке  на место ), иначе говоря, собственным значением матрицы . Соответственно

  и решение системы уравнений (12) является положительным.

Вместе с тем роль матрицы  состоит не только в реализации условия неразложимости. Под воздействием интеллектуально-информационных потоков исходная матрица  будет некоторым образом оптимизироваться, приобретая вид

(где нулевые элементы располагаются аналогично ).

Условия (13) можно представить следующим образом:

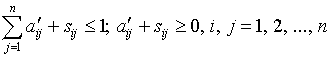,                                                      (14) из общих соображений, полагая, что для большинства сочетаний  

, (15) то есть, использование интеллектуальных продуктов позволяет сокращать издержки производства. Критерий эффективности кластера в таком случае мог бы иметь обобщенный характер вида

.

Из неравенств (13) – (15), вытекает целесообразность минимизации денежного эквивалента интеллектуально-информационных ресурсов. Но, в свою очередь, ими определяется повышение экономичности за счет перехода от матрицы  к . Таким образом, возникает своеобразная задача оптимизации, для разрешения которой, как представляется, наиболее адекватна методология [23], рационально синтезирующая информационно-алгоритмическую сложность со стоимостью практической реализации.

В этой связи отметим также замечание Р.Беллмана и С.Дрейфуса о том, что ценность информации может измеряться в категориях эффективности решений, которые с ее помощью принимаются [24, с. 342].

На основании приведенных соображений становится очевидным, что определение  в качестве матрицы интеллектуально-информационных потоков не является вполне точным. Действительно, главную роль, оказывается, играют не объем и стоимость нематериальных активов, а эффективность их использования для практических целей.

Вследствие этого мы приходим к выводу о том, что кластер должен иметь координирующий орган, который бы оперативно осуществлял сбор, обработку информации и принятие управленческих решений. Включая стимулирование лишь объективно необходимых взаимодействий между участниками. В таком случае потоки, соответствующие матрице , логично охарактеризовать как информационно-аналитические.

Упростим теперь ситуацию, полагая , что характерно для начального этапа развития кластера. Соответственно система уравнений (12) приобретает вид

; из сопоставления с (1), а также вследствие неразложимости матрицы  и (11), (13) вытекает, что , или же все  (такие варианты лишают рассуждения содержательного смысла). В противном случае при неизменном векторе  стоимость продукции  должна возрасти за счет увеличения издержек производства и, конечно, подобная возможность является нежелательной.

Таким образом, в подтверждение сказанного выше, можно сделать еще более конкретный вывод о том, что интенсивности потоков  должны быть минимально приемлемыми. Иначе говоря, информацию следует рационально дозировать (что представляет собой достаточно нетривиальную задачу). Естественно, возникает вопрос об оценке такой приемлемости, в связи с чем, следует отметить:

- матрица  должна быть неразложимой, иначе позитивные качества системы уравнений (12) в значительной мере утрачиваются;

- свойство неразложимости  достигается за счет  – матрицы информационно-аналитических потоков;

-  выстраивается на основе  – матрицы материально-финансовых потоков;

- для создания кластера необходимо проведение работ по привлечению потенциальных участников, сбору и обработке соответствующей информации.

На этом основании, минимальный эквивалент стоимости потоков матрицы  предопределяют факторы:

1. Склонность участников к предоставлению достоверной информации по матрице .

2. Организационно-управленческий профессионализм координирующего органа.

3. Осознание неразрывного единства понятий «кластер» и «неразложимость матрицы ».

Первый из этих факторов является основополагающим. Как представляется, именно в нем заключается главное преимущество и уникальность кластера, как организационно-экономической системы. Соответственно идентификацию матрицы стоимостного баланса следует рассматривать в качестве одной из определяющих компонент понятия «кластер». На пути создания кластера в части морально-психологических и транзакционных аспектов могут потребоваться значительные издержки, которые не отнесены нами к матрице .

Последний из указанных выше факторов подразумевается в его практической реализации посредством эффективной деятельности организационно-управленческого звена. Заметим также, матрица  останется неразложимой, если принять , где  и , такие, что . Это наблюдение приводит к не совсем очевидному выводу: в первую очередь, при создании кластера должны прилагаться усилия по развитию взаимодействий между участниками, которые не имеют прямых контактов по технологическому признаку.

Очевидно, при управлении текущей деятельностью кластера весьма важную роль играет следующее обстоятельство. Математические теоремы никак не гарантируют, что в какой-то период времени стоимость продукции одного из участников окажется ниже себестоимости производства, тогда как другой может сбыть ее внешнему потребителю, нарушая внутренние взаимосвязи, по более высокой цене.

Кроме того, некоторые из участников могут представлять собой неприбыльные организации, но их нельзя заменить, а деятельность, например, координирующего органа трудно поддается оценке в стоимостном эквиваленте.

Подытоживая приведенные соображения, можно сделать следующие выводы:

1. Деятельность финансово неприбыльных участников должна с повышенной аккуратностью и неформально учитываться при исследовании систем уравнений стоимостного баланса.

2. Критерием результативности кластера является сумма элементов вектора внешнего спроса , которая подлежит перераспределению между участниками.

3. Для этого, в дополнение к общей ментальности кластера [10], существует специальный аппарат согласования позиций сторон и поддержки принятия решений (см. [19, 25 – 28]).

4. Итак, кластеру объективно присуще функционирование в рамках механизма внутренних цен, что следует отнести к одному из его конкурентных преимуществ.

5. Приведенные выше соображения в отношении матриц  и , являясь весьма важными для раскрытия уникальных особенностей кластера, тем не менее, носят качественный характер.

6. Их следует трактовать в качестве доказательства существования конкурентных преимуществ экономического кластера, однако, при условии эффективного сотрудничества и координации действий его участников.

7. В этом процессе социальная (гуманитарная) компонента кластера выполняет функции механизма эффективной адаптации отношений экономического партнерства.

Для реализации стратегии кластера в целом, а также определения внутренних цен целесообразно использовать вариативные расчеты на базе системы уравнений (1), учитывая следующие предпосылки:

- матрица  неразложима за счет присутствия минимальных значений  на месте ;

- свободные члены  и коэффициенты  определены посредством оптимизации и других инструментов;

- суммы элементов каждой из строк матрицы  не превосходят или меньше единицы.

При этом обобщенную схему управления деятельностью кластера можно представить в разрезе расчетно-аналитического сопровождения:

- определение стоимости единиц  видов продукции, выходящей на внешнего потребителя, и в сопоставлении с гарантированной ликвидностью – значений , характеризующих конкурентоспособность;

- определение доли участников в «активе» и «пассиве» посредством соответствующих соотношений между величинами  и ;

- ликвидация «пассива» средствами сокращения «актива» до рыночного уровня, включая аналогичную оценку долей участников;

- проверка выполнения интегрального критерия результативности кластера, а именно

,                                                                                                       (16) где – суммарный дисконт, с позиций долей участников и удовлетворения их интересов;

- повторение расчетов в привязке к (16) для вариантов снятия с производства неконкурентоспособного вида продукции, установления договорных стоимостей части , перераспределения коэффициентов  и т. п.;

- установление внутренних цен на продукцию и услуги участников с использованием также механизмов согласования позиций сторон, присущих кластеру.

С помощью обозначенного алгоритма участникам кластера предоставляется конструктивная возможность для оценки влияния своих действий на конечные результаты и рациональной выработки управленческих решений. Вместе с тем, на этапе создания кластера потенциальные участники получают инструмент, позволяющий прогнозировать конкурентные преимущества своей организации.

Однако весьма информативными могут быть и гораздо более простые оценки, о чем свидетельствует материал заключительного раздела. В этой связи, предварительно, на простом примере проиллюстрируем преимущества, которые может приносить сотрудничество субъектов экономической деятельности.

Имеются два субъекта, работающие самостоятельно. Для большей прозрачности, предположим, что их затраты одинаковы и рентабельность каждого (по отношению к цене) составляет 20%:

, откуда

, где  и  – доходы субъектов.

В результате совместной деятельности согласно

                                                                                    (17) (то есть, при тех же затратах и рентабельности каждого) получаем

.

Таким образом, затраты остались без изменения, в размере , а суммарный доход увеличился до в  раза. Однако в точно такой же пропорции возросла суммарная стоимость  продукции субъектов (ставших теперь участниками экономической системы). Возникает резонный вопрос – можно ли при таком росте, даже теоретически, обеспечить конкурентоспособность продукции?

Вместе с тем, конкурентоспособность определяется стоимостью единицы продукции, или же ценой

,

где  – объем производства в натуральном выражении. Поэтому в эффективной системе вида (17) ликвидность производимой участниками продукции и фактический рост их рост доходов  могут достигаться за счет соответствующего увеличения объемов .

Очевидно с увеличением порядка матрицы , выстраиваемой по аналогии с (17), тенденция охарактеризованного роста доходов будет проявляться в еще большей степени. При этом конечно, матрица  не должна быть вырожденной; более тонкие моменты такого рода условий освещает теория положительных решений операторных уравнений [29, п.4].

По существу, решение приведенного примера олицетворяет собой метод количественной оценки синергетического эффекта, реализация которого потенциально возможна в экономической системе. Однако следует подчеркнуть, в качестве такой системы может выступать только кластер, иначе нам не известна матрица  и проведение расчетов утрачивает смысл.

4. Иллюстрация эффективности кластерного подхода к организации экономической деятельности*

Приведем ряд расчетных оценок, которые производились в процессе конструирования кластера молочного профиля. Рассматривается система, включающая семь основных участников, связанных отношениями технологического партнерства. Их специализация:

№1 – производство кормов;

№№ 2, 3 – производство молока;

№4 – производство сыров;

№5 – производство цельномолочной продукции;

№№ 6, 7 – реализация сыро-молочной продукции.

Для воплощения этой системы в кластер необходимо показать достигаемые таким образом преимущества. Воспользуемся моделью (1) с , соответственно матрица

.                                                                                  (18)

Задача 1. Участники №№ 1-5 не выходят на внешнего потребителя, то есть , . Вклад (часть от реализации внешнему потребителю) и доход участников №№ 6, 7 составляют соответственно: ;  (миллионов гривен) и ; . Упомянутая часть от реализации распределяется между участниками №№ 4, 5 следующим образом:

.                                                                      (19)

Других источников поступления средств участники №№ 4, 5 не имеют и соответственно

;                                            (20) в свою очередь, они получают доход  и , а с участниками №№ 2, 3 производят расчет следующим образом:

.                                                         (21)

Заметим, что на основании цен производителя и продаж конечному потребителю участники №№ 4, 5 могут точно судить о «справедливости» коэффициентов , . Однако ситуация во взаимоотношениях переработчиков, производителей молока и кормов является весьма непрозрачной. Не раскрывая реальную себестоимость производства, участники могут ориентироваться лишь на сложившиеся рыночные цены.

Но какие для этого были побудительные причины и как они сказались на рентабельности технологических партнеров в смысле «справедливости» разделения дохода от реализации – непонятно. Не зная себестоимости переработчиков и торговцев, участники № 2, 3 фактически устанавливают цены своей продукции, исходя из себестоимости ее производства и цен сыро-молочной продукции для конечного потребителя. Аналогично и участник №1 не знает себестоимости производителей молока.

Участники №№ 2, 3 также получают доход в размере  и , а с участником №1 производят расчет, определяемый коэффициентами

;                                                                                          (22) одновременно  представляет собой доход этого участника. О коэффициентах  будет сказано ниже.

В результате матрица (18) приобретает вид

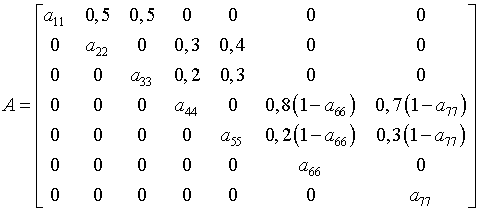.                        (23)

Нетрудно заметить, что вследствие большого количества нулевых элементов этой матрицы система уравнений (1) распадается. То есть, вычисление значений  может осуществляться последовательно:

; способствуя большей наглядности рассматриваемой задачи в ее исходной постановке, этот фактор затем продемонстрирует очень интересные эффекты.

Итак, охарактеризована ситуация технологического партнерства, когда участники не сообщают друг другу размер своей рентабельности. Тем не менее, все они заинтересованы в конкурентоспособности конечной продукции и хотели бы иметь расчетный аппарат для проведения соответствующей оценки. Рассмотрим случай, когда рентабельность всех участников, на самом деле, одинакова и изменяется в пределах от 0 до 50%, то есть

,                                                                  (24) предполагая, что объемы производства продукции при этом остаются неизменными. Зависимость стоимостей продукции участников от их рентабельности, найденная путем решения системы линейных алгебраических уравнений (1) с матрицей (23), показана на рис. 1.

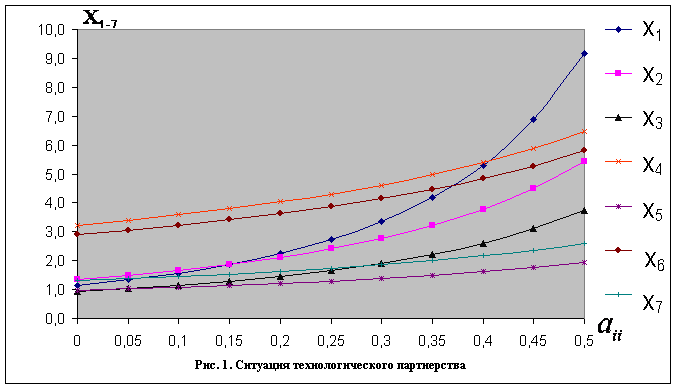
Как можно заметить, лишь в сравнительно небольшом диапазоне возрастания  полученные результаты соответствуют логике процесса создания стоимости конечной продукции. Иначе говоря, цены торговцев должны быть выше стоимости сыров и цельномолочной продукции у производителей. Продукция переработчиков, в свою очередь, дороже, чем молоко. Стоимость молока выше по сравнению с кормами, которые пошли на его производство.

Однако из-за диспропорций в сопряжениях между участниками №№ 4, 5; №№ 2, 3 и №1 с ростом  наблюдается явный перекос распределения суммарно создаваемой стоимости в пользу производителей молока и кормов. Начиная с некоторого значения , стоимость кормов достигает стоимость конечной продукции и соответственно деятельность такой системы становится абсурдной.

Задача 2. Предположим, что в отличие от предыдущего случая участники договорились между собой об оплате получаемой продукции с сохранением существовавших пропорций (которые указаны выше), однако за вычетом получаемых ими доходов. Иначе говоря, все взаимоотношения становятся такими же, как между участниками №№ 4, 5 и №№ 6, 7. При этом соотношения (19) и равенства (20) остаются в силе, а вместо (21) и (22) получаем:

; соответственно изменятся элементы строк 1-3 матрицы (23).

Если реальные рентабельности участников удовлетворяют условию (24), решение системы уравнений (1) становится таким, как показано на рис. 2. Нетрудно сделать вывод о том, что эта экономическая система не содержит внутренних противоречий. Ее можно охарактеризовать как объективно присущую организации кластерного типа, в которой участники предоставляют друг другу достоверные сведения о финансово-хозяйственной деятельности.

Задача 3. Однако обе рассмотренные постановки задач предполагали возможность повышения рентабельности участников за счет роста стоимости конечной продукции. В действительности это, как правило, является невозможным. Если теперь предположить, что рентабельность достигаться участниками за счет повышения экономичности производства и услуг (интерпретируемого как вложение внутренних ресурсов), то приходим к решению системы уравнений (1) относительно теперь уже показателей себестоимости  с матрицей следующего вида:

.

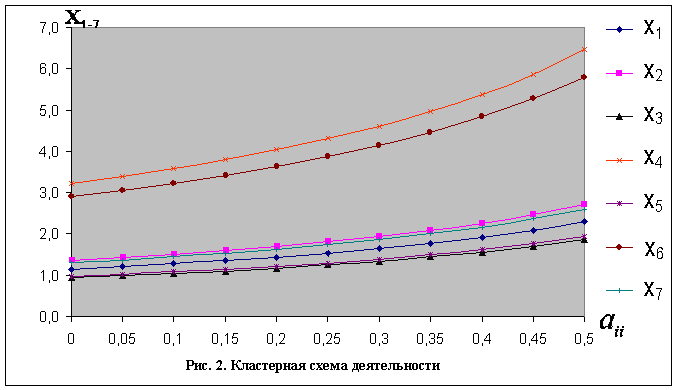
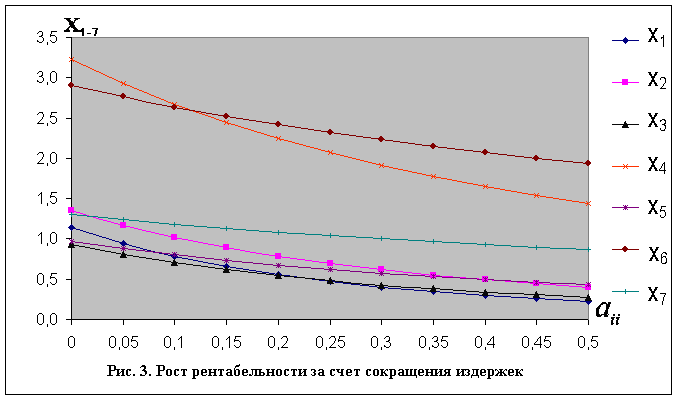
Снижение себестоимости продукции, которое необходимо для роста рентабельности согласно (24), характеризует рис. 3.

Здесь отражен вполне реалистичный факт более быстрого снижения себестоимости производителей по сравнению с предприятиями торговли. Суть в том, что за счет себестоимости производителей компенсируется не только повышение их собственной экономичности, но также и аналогичные процессы в торговой сети. С учетом, естественно, коэффициентов, пропорциональных частям передаваемой на реализацию продукции. Подчеркнем, что подразумевается не собственно себестоимость производства, а информативно характеризующий ее показатель.

Задача 4. Эта и последующая постановки задач имеют, по сравнению с теми, которые рассмотрены выше, иной характер, а именно рентабельность участников в каждом случае принимается постоянной. Предположим, что их взаимодействие определяется матрицей (18) следующего вида:

,                                                  (25) то есть, рентабельность каждого участника составляет 10%. При этом свободный член первого из уравнений (1) может изменяться в пределах . Иначе говоря, производитель кормов продает их не только участникам рассматриваемой системы, но и внешнему потребителю. Вид решения в этом случае достаточно очевиден, рис. 4.

Он является ориентиром, который позволит судить о том, какие изменение произойдут в системе, если торговле кормами станут оказывать содействие участники №№ 6, 7 (профессионалы этого вида деятельности), получая вознаграждение согласно

.                                                                                          (26)

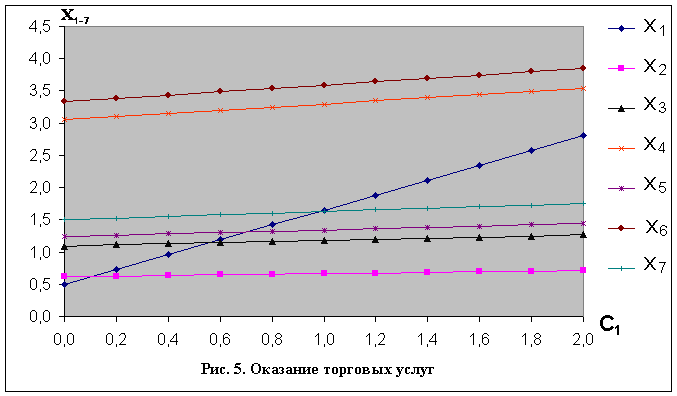
При подстановке этих коэффициентов в (25) система уравнений (1) перестает быть «распадающейся» (см. сказанное выше); ее решение приобретает вид, показанный на рис. 5. Как нетрудно заметить, распределение стоимостей продукции

участников значительно изменилось. Действительно, в системе появились дополнительные расходы на торговлю и участники №№ 6, 7 от этого выиграли.

Но наряду с этим, резко возросла стоимость продукции участника №4 (производитель сыров), что явилось достаточно неожиданным. Темп роста  оказался практически таким же, как  и гораздо большим по сравнению с  (торговля). В свою очередь, рост близкий к участнику №7, продемонстрировали участники №№ 2, 3 и 5, непосредственно от продажи кормов ничего не получающие.

Представим теперь всего лишь минимальные отклонения от нуля тех же коэффициентов (26), а именно:

,                                                                                     (27) приводящие к решению, показанному на рис. 6.

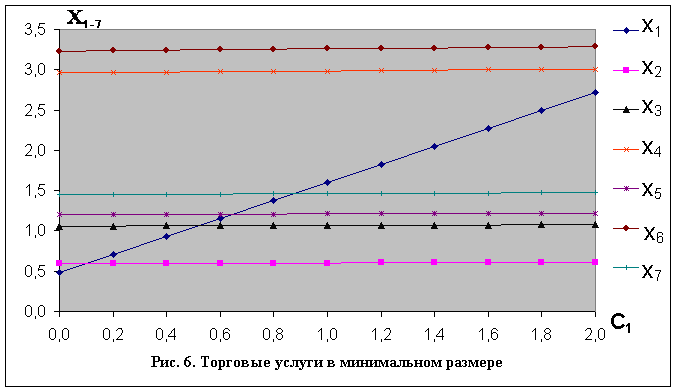
Однако и в этом случае стоимость продукции участника №4 выходит точно на ту же отметку, что в предыдущем. Достаточно сопоставить данные рис. 5 и 6, а также рис. 4. Претерпела изменение лишь динамика роста в зависимости от значения . На первый взгляд, совсем незначительные изменения коэффициентов , , привели, тем не менее, к резкому изменению функции . Едва ли такой результат можно было прогнозировать без проведения расчетной оценки.

С предметной точки зрения, за этим – явная неэффективность организации экономических отношений в рассматриваемой системе и, более того, она является неустойчивой (см. материал п.2). В самом деле, элементы (27) на порядок меньше по сравнению с (26) и соответствующая матрица  очень близка к (25), однако эффект, вызванный их появлением, оказался столь же значительным (подразумевается сопоставление с данными рис. 4).

Парадоксальный результат получается в гипотетическом варианте 90%-ной рентабельности всех участников, рис. 7. Для поддержания баланса системы все участники, за исключением №2, должны дотироваться извне. Конечно, модель экономической системы, образованной на основе матрицы (25), в условиях высокой рентабельности участников является нежизнеспособной.

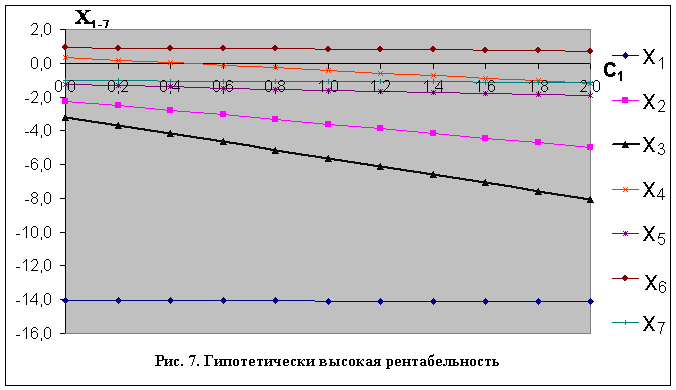
Объяснение состоит в том, что суммы элементов каждой из строк этой матрицы при  больше единицы, вследствие чего условие положительности решения системы уравнений (1):

  не выполняется (см. п.1).

Задача 5. Пусть теперь, в условиях предыдущей постановки экономическая система представляет собой кластер, порождающий матрицу задачи 2. При  получаем

;                                      (28) решения для случаев, когда элементы ,  определяются согласно (26) и (27), показаны на рис. 8 и 9 соответственно.

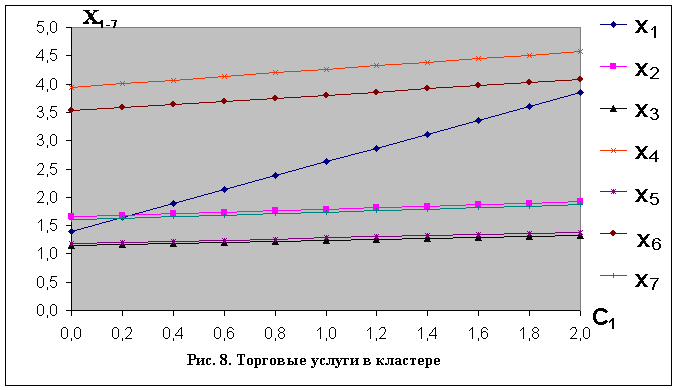
На основании сопоставления значений , представленных на рис. 8, 9, со значениями  при  рис. 2, можно сделать вывод о том, что в случае организации кластерного типа, то есть когда во взаимоотношениях участников учтены реально получаемые ими доходы, поведение экономической системы является вполне прогнозируемым. Действительно, отсутствует сильная зависимость решений от малых изменений данных задачи, исчез безосновательный скачок функции .

Задача 6. Вновь рассматривается матрица (25), но вместо свободного члена  изменяется . Иначе говоря, участник №2 продает свое молоко не только участникам №№ 4, 5, но также и внешнему потребителю. Из решения, показанного на рис. 10, вообще говоря, вытекает противоречие, состоящее в том, что вместе с ростом стоимости молока растет также и стоимость кормов. Очевидно, постановка задачи требует уточнения в том плане, может ли участник №1 обеспечить необходимые объемы производства кормов, или же понадобится подключение сторонних субъектов. В таком случае размер матрицы  увеличится.

Далее предполагается, что объемы кормов, адекватные росту , обеспечиваются исключительно участником №1. Кроме того, участники №№ 6, 7 аналогично предыдущему получают вознаграждение за помощь в торговле:

; ; .                (29)

Заметим, что если в этом случае рентабельность является очень высокой, то для указанных значений ,  получаем решения, еще более абсурдные, чем на рис. 7. Система «накачивается» средствами извне в гораздо большем размере, причем лидером является все тот же производитель кормов.

Решения системы уравнений (1) с матрицей (28) и элементами , , которые определяются согласно (29), показаны на рис. 11 и 12 соответственно.

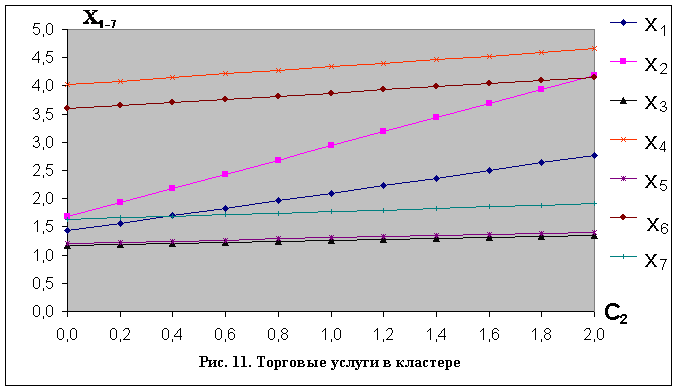
На основании сопоставления с данными рис. 2, можно сделать вывод о том, что они вполне удовлетворительно отражают логику функционирования экономической системы.

Рассматривались также постановки задач с учетом факторов:

- стимулирование участниками развития кормопроизводства;

- зависимость рентабельности торговцев от объемов реализации;

- взаимодействие между переработчиками молока.

Выводы

Модель Леонтьева, в стоимостной интерпретации, порождает класс матриц, теория которых является весьма конструктивной. Вследствие этого появляется возможность для оценки эффективности структурного устройства и процессов, происходящих в кластере, а также оптимизации управленческих решений.

Уникальность кластера, как организационно-экономической системы, а также решающий фактор его конкурентоспособности, обусловлены возможностью идентификации матрицы материально-финансовых потоков (включая реальные доходы), вследствие доверительных взаимоотношений участников.

В этой связи предложена обобщенная схема управления деятельностью кластера, включающая алгоритм определения внутренних цен на продукцию участников с использованием расчетных средств и механизмов согласования позиций сторон, которые объективно присущи кластеру.

В общем случае, матрицы баланса могут проявлять свойства неустойчивости под воздействием малых возмущений. Данное обстоятельство служит убедительным основанием для того, чтобы присоединиться к известному мнению об объективной неустойчивости экономической системы в условиях совершенной конкуренции.

В процессе управления деятельностью кластера необходимо стремиться к тому, чтобы он соответствовал модели Леонтьева, удовлетворяющей (в определенном смысле) условиям 2-й теоремы Перрона-Фробениуса. При возникновении различного рода отклонений они должны быть в каждом случае предметно интерпретированы и затем устранятся посредством координации действий участников.

Литература

1. Моришима М. Равновесие, устойчивость, рост (Многоотраслевой анализ). – М.: Наука, 1972. – 279 с.

2. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. – М.; Л.: Физматгиз, 1963. – 734 с.

3. Стренг Г. Линейная алгебра и ее применения. – М.: Мир, 1980. – 454 с.

4. Воеводин В.В. Вычислительные основы линейной алгебры. – М.: Наука, 1977. – 303 с.

5. Беллман Р. Введение в теорию матриц. – М.: Наука, 1969. – 367 с.

6. Маркус М., Минк Х. Обзор по теории матриц и матричных неравенств. – М.: Наука, 1972. – 232 с.

7. Ланкастер П. Теория матриц. – М.: Наука, 1978. – 280 с.

8. Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. – М.: Наука, 1984. – 318 с.

9. Писсанецки С. Технология разреженных матриц. – М.: Мир, 1988.  – 411 с.

10. Портер М. Конкуренция. – СПб: Изд. дом «Вильямс», 2001. – 495 с.

11. Соколенко С.И. Производственные системы глобализации: Сети. Альянсы. Партнерства. Кластеры: Украинский контекст. – К.: Логос, 2002. – 645 с.

12. Андрощук Г.А. Оценка промышленной и интеллектуальной собственности //Государственный бюллетень о приватизации. – 1997. – №1.  – С. 59-71.

13. Горячковская Н. Объекты интеллектуальной собственности (Методы и способы ценообразования) //Бизнес Информ. – 1998. – №7. – С. 46-50.

14. Кемпбелл Э., Саммерс Лаче К. Cтратегический синергизм. – СПб: Питер, 2004. – 414 с.

15. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. – М.: Мир, 1980. – 454 с.

16. Хорн Р., Джонсон Ч. Матричный анализ. – М.: Мир, 1989. – 655 с.

17. Грегори Р., Кришнамурти Е. Безошибочные вычисления. Методы и приложения. – М.: Мир, 1988. – 208 с.

18. Парлетт Б. Симметричная проблема собственных значений. Численные методы. – М.: Мир, 1983. – 382 с.

19. Мулен Э. Кооперативное принятие решений: Аксиомы и модели. – М.: Мир, 1991. – 463 с.

20. Икрамов Х.Д. Несимметричная проблема собственных значений. Численные методы. – М.: Наука, 1991. – 240 с.

21. Малышев А.Н. Введение в вычислительную линейную алгебру. – Новосибирск: Наука, 1991. – 228 с.

22. Фильштинский В.А., Фильштинский С.В. Взаиморасчет, взаимозачет, коллективные сделки. – Харьков: Бизнес Информ, 1996. – 91 с.

23. Трауб Дж., Васильковский Г., Вожьняковский Х. Информация, неопределенность, сложность. – М.: Мир, 1988. – 183 с.

24. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. – М.: Наука, 1965. – 458 с.

25. Саати Т., Кернс К. Аналитическое планирование. Организация систем. – М.: Радио и связь, 1991. – 224 с.

26. Моисеев Н.Н. Математические задачи системного анализа. – М.: Наука, 1981. – 487 с.

27. Гермейер Ю.Б. Игры с непротивоположными интересами. – М.: Наука, 1976. – 327 с.

28. Управление по результатам /Т.Санталайнен, Э.Воутилайнен, П.Поренне, Й.Х.Ниссинен. – М.: ИГ «ПРОГРЕСС», «УНИВЕРС», 1993.– 319 с.

29. Интегральные уравнения /П.П.Забрейко, А.И.Кошелев, М.А.Красносельский и др. – М.: Наука, 1968. – 448 с.

* Расчеты выполнены А.О.Гаревым, НТУ «ХПИ»