Коваленко О.Г.

Использование аппарата теории массового обслуживания для решения экономических задач

В статье рассматриваются методы экономико-математического моделирования, которые широко используются в различных областях экономики, при принятии управленческих решений в финансовой сфере в силу разработанности математического аппарата и возможности практической реализации.

Применение математических методов требует:

* системного подхода к исследованию заданного объекта, учета взаимосвязей и отношений с другими объектами (предприятиями, фирмами);

* разработки математических моделей, отражающих количественные показатели системной деятельности работников организации, процессов, происходящих в сложных системах, какими являются предприятия;

* совершенствования системы информационного обеспечения управления предприятием с использованием электронно-вычислительной техники.

На рисунке 1 приведены основные математические методы, применяемые в экономическом анализе.

Теория массового обслуживания, как раздел исследования операций, на основе теории вероятности исследует математические методы количественной оценки процессов массового обслуживания. Особенность всех задач, связанных с массовым обслуживанием, — случайный характер исследуемых явлений. Количество требований на обслуживание и временные интервалы между их поступлениями имеют случайный характер, однако в совокупности подчиняются статистическим закономерностям, количественное изучение которых и есть предмет теории массового обслуживания

Рисунок 1 - Классификация основных математических методов, применяемых в экономическом анализе

Примерами систем массового обслуживания (СМО) могут служить:

• посты технического обслуживания автомобилей;

• посты ремонта автомобилей;

• персональные компьютеры, обслуживающие поступающие заявки

или требования на решение тех или иных задач;

• станции технического обслуживания автомобилей;

• аудиторские фирмы;

• отделы налоговых инспекций, занимающиеся приемкой и

проверкой текущей отчетности предприятий;

• телефонные станции и т. д.

В качестве основных критериев эффективности функционирования СМО в зависимости от характера решаемой задачи могут выступать:

• вероятность немедленного обслуживания поступившей заявки;

• вероятность отказа в обслуживании поступившей заявки;

• относительная и абсолютная пропускная способность системы;

• средний процент заявок, получивших отказ в обслуживании;

• среднее время ожидания в очереди;

• средняя длина очереди;

• средний доход от функционирования системы в единицу времени и т. п.

Независимо от характера процесса, протекающего в системе массового обслуживания, различают два основных вида СМО:

• системы с отказами, в которых заявка, поступившая в систему в момент, когда все каналы заняты, получает отказ и сразу же покидает очередь;

• системы с ожиданием (очередью), в которых заявка, поступившая в момент, когда все каналы обслуживания заняты, становится в очередь и ждет, пока не освободится один из каналов.

Рассмотрим частный случай системы с ожиданием - одноканальную СМО с ожиданием. Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание - простейший поток с интенсивностью . Длительность обслуживания – h - случайная величина, подчиненная показательному закону распределения. Поток обслуживания является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.

Рисунок 2 – Граф состояний одноканальной СМО с ожиданием

Состояния СМО имеют следующую интерпретацию:

 — канал свободен;

— канал занят (очереди нет);

 — канал занят (одна заявка стоит в очереди);

 - канал занят (п -1 заявок стоит в очереди);

 - канал занят (N-1  заявок стоит в очереди).

Определим характеристики одноканальной СМО с ожиданием:

1. Вероятность ожидания обслуживания:

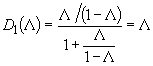
2. Обслуженная нагрузка (пропускная способность):

3. Средняя длина очереди:

4. Среднее время ожидания обслуживания:

Рассмотрим применение теории массового обслуживания на следующем примере. В магазине работает один продавец, который обслуживает одного покупателя в среднем за 2 минуты. Поток покупателей простейший с интенсивностью, равной 20 покупателям в час (). Необходимо определить следующие вероятностные характеристики магазина для стационарного режима работы: абсолютную пропускную способность магазина; среднюю длину очереди; среднее время ожидания в очереди;

вероятность простоя продавца.

Решение.

1. Пропускная способность магазина:

 (покупателя в минуту)

2. Средняя длина очереди:

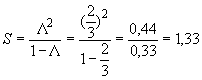(покупателя)

3. Среднее время ожидания в очереди:

(минуты)

4. Вероятность простоя продавца:

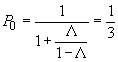
Математические методы ускоряют проведение экономического анализа, способствуют более полному учету влияния факторов на результаты деятельности, повышению точности вычислений.

                               Литература:

1. Айвазян С.А., Мхитарян В.С. :прикладная статистика и основы экономики: Учебник-М.:ЮНИТИ,1998

2. Лабскер Л.Г., Бабешко Л.О.: Теория массового обслуживания в экономической сфере: Учебное пособие- М.: ЮНИТИ, 1998

3. Бережная Е.В., Бережной В.И.: Математические методы моделирования экономических систем: Учебное пособие- 2-е издание; перераб. и доп.- М.: Финансы и статистика, 2006-432с.: ил.