Жураковская А.В.
Моделирование логистических процессов
Движение материальных потоков на предприятии осуществляется квалифицированным персоналом с помощью разнообразной техники: транспортные средства, погрузочно-разгрузочные устройства и т. д. В этот логистический процесс вовлечены различные здания и сооружения, ход же самого процесса существенно зависит от степени подготовленности к нему, самих движущихся и периодически накапливаемых в запасах грузов. Совокупность производительных сил, обеспечивающих прохождение грузов, лучше или хуже, но всегда как-то организована. По существу, если имеют место материальные потоки, то всегда имеет место какая-то материалопроводящая система. Традиционно эти системы специально не проектируются, а возникают как результат деятельности отдельных элементов. Рассмотрим классический пример задачи с материалопроводящим потоком – транспортную задачу. [4]Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Классическая транспортная задача – это задача нахождения оптимального плана перевозок однородного продукта или взаимозаменяемых продуктов из пунктов производства в пункты потребления, и встречается чаще всего в практических приложениях линейного программирования. Линейное программирование является одним из разделов математического программирования – области математики, разрабатывающей теорию и численные методы решения многомерных экстремальных задач с ограничениями. [2]
В зависимости от способа представления условий транспортной задачи она может быть представлена в сетевой (схематичной) или матричной (табличной) форме. Транспортная задача может также решаться с ограничениями и без ограничений. [3]
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления А1, А2, ..., Аm в n пунктов назначения В1, В2, ..., Вn. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим ТЗ, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза.
Пусть cij – это тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, аi – запасы груза в i-м пункте отправления, bj – потребности в грузе в j-м пункте назначения, xij –количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции
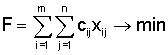
при условиях
Поскольку переменные xij (
;) удовлетворяют системам линейных уравнений и условию неотрицательности, обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки. [3]
Для решения данной задачи применяется метод потенциалов, который является упрощенным вариантом модифицированного симплекс-метода .
Таким образом, правильно формализованная транспортная задача позволяет получить рациональные результаты при построении оптимизационной модели, что, в свою очередь, на практике позволяет сократить транспортные расходы. Сокращение транспортных расходов очень выгодно отражается на себестоимости продукции, перевозимой данным транспортом, а так же на себестоимости продукции, составляющие которой перевозятся данным транспортом. Это, в свою очередь, позитивно влияет на формирование чистой прибыли.
Литература:
1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высш.шк., 1986. – 320 с.
2. Акоф Р., Сасиени М. Основы исследования операций. М. Мир, 1971
3. Вагнер Г. Основы исследования операций, т.1. М., Мир, 1972; т. 2-3. М., 1973.
4. Гольштейн Е.Г., Юдин Д.Б. Новые направления в линейном программировании. М., Наука, 1966.