Ширяев А.Ю.
Об оценивании параметров распределений и проверке гипотез по цензурированным выборкам
Методы оценивания параметров модели, проверка ее адекватности, проверка различных гипотез о параметрах или составляющих модели опираются на имеющуюся априорную информацию, на количество и структуру наблюдений, характеризующих состояние системы. После того, как высказаны предположения о характере вероятностной модели, на основе имеющихся наблюдений обычно решают два вида задач статистического анализа. Во-первых, стараются оценить параметры этой модели таким образом, чтобы она с наибольшей точностью описывала соответствующее явление. Во-вторых, с использованием некоторого критерия проверяют адекватность модели данному явлению. Если модель представляет собой закон распределения, то проверка осуществляется с использованием некоторого критерия согласия. На этапе такой проверки с минимальными вероятностями ошибок гипотеза об адекватности модели должна быть принята, если это действительно так, или отклонена в пользу другой модели, более подходящей. Цель такой проверки – уловить отклонения модели от “истинной”, если они есть, а не постараться их не заметить.Специфика задач надежности, физическая сущность конкретной предметной области учитываются на этапе выбора вида модели, а методы статистического анализа при этом опираются на вид модели и структуру наблюдаемых данных. В задачах надежности очень часто имеют дело с цензурированными выборками. При этом, вследствие потерь информации из-за цензурирования снижается качество статистических выводов: труднее идентифицировать модель и различать близкие законы распределения, снижается точность оценивания параметров. В то же время при вычислении по цензурированным выборкам оценок максимального правдоподобия (ОМП) сталкиваются со значительной смещённостью оценок, при этом величина смещения зависит от степени цензурирования и от объёма выборки. При достаточно больших объёмах выборок (возможно применение критериев типа 
(Пирсона, Никулина). При простых гипотезах и цензурированных наблюдениях для проверки могут использоваться критерии Реньи, которые в этой ситуации являются “свободными от распределения”. Однако очевидно, что при проверке сложных гипотез они теряют это свойство и, следовательно, необходимы соответствующие исследования распределений их статистик. Отметим кстати, что в этих статистиках вполне обосновано с наибольшим весом берутся наблюдения вблизи точек цензурирования. Применимость критериев согласия типа типа Колмогорова и типа 
Мизеса при цензурированных наблюдениях также требует дополнительных исследований. При этом следует иметь в виду, что проверка сложных гипотез тесно взаимосвязана с проблемой оценивания параметров.
При условии, что будет реализован алгоритм эффективного решения первой задачи, решение второй не вызывает в настоящий момент принципиальных трудностей, так как с помощью методов статистического моделирования и с использованием возросших возможностей компьютерной техники с достаточной для практического применения точностью могут быть построены приближенные модели предельных распределений статистик.
То, что касается возможной точности оценивания, то для ОМП скалярного параметра она ограничивается снизу асимптотической дисперсией
где n – объем выборки. Информационное количество Фишера по цензурированной выборке определяется соотношением
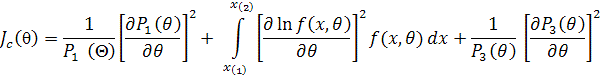
где – вероятность попадания в область цензурирования слева, 
- вероятность попадания в область цензурирования справа, а наблюдаемая область лежит в пределах от до 
. Если выборка цензурирована только справа, то в выражении исчезает левое слагаемое, только слева - правое слагаемое. Это соотношение позволяет судить о потерях информации о параметре распределения в зависимости от степени цензурирования слева или справа и возможной точности оценивания. Чем больше потери информации, тем меньше возможная точность оценивания.
Об эффективности оценивания параметров по цензурированной выборке по отношению к оцениванию по полной выборке (без цензурирования) можно судить по величине , где 
– количество информации Фишера по полной выборке.