Конина О.В.

Контроль качества в образовании: математический аспект

К базовым математическим моделям контроля качества образовательного процесса относятся: бальная, нормативно-классификационная, эталонная модели и модель ранжирования объектов системы образования.

R = α1Х1 + α2Х2 + … + αnХn             (1)

где αi – весовые множители, назначаемые экспертами эвристически (экспертный опрос).

Преимущества рассматриваемой модели заключаются в ее простоте и малой трудоемкости, однако выделяется ряд недостатков:

1) необходимость выбора весовых множителей экспертным путем;

2) суммирование величин, имеющих разные размерности;

3) невозможность оценки степени реализации потенциала.

В нормативно-классификационной модели рейтингов [1] вся совокупность исходных показателей состояния и активности  деятельности заданного объекта разделяется на два множества показателей:

2) показатели активности и результативности, характеризующие результаты функционирования данного объекта за предшествующий период планирования (подразделяются на виды деятельности).

Показатели потенциальных возможностей и видов деятельности каждой из групп нормируются относительно некоторых величин, имеющих экономический смысл. Для каждой группы потенциальных возможностей и вида деятельности экспертным методом определяются весовые коэффициенты, и осуществляется вычисление рейтингов потенциалов по различным видам потенциальных возможностей и рейтингов активности по различным видам деятельности.

Профессором В.И.Чернецким была предложена эталонная модель управления большими системами управления [2], сущность которой заключается в предположении о том, что можно выбрать некоторый идеальный (эталонный) объект управления, значения параметров которого являются оптимальными в том или ином смысле. Затем значения контролируемых параметров всех других объектов управления, относящихся к тому же типу, что и эталонный объект, оцениваются по отклонениям от значений параметров эталонного объекта. На основе результатов сравнения фактических и эталонных значений контролируемых параметров синтезируется дополнительный контур управления (контур самонастройки), основной целью которого является последовательное изменение некоторых технологических параметров, определяющих динамику движения объекта в необходимом направлении.

В модели ранжирования объектов системы высшего образования рассчитывается интегральное качество исследуемого объекта с помощью ком­плексного интегрального показателя качества, основанного на объективной значимости каждого фактора:

R(Аi) = 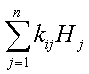             (2)

где R(Аi) - интегральное качество объекта Аi, m - количество объектов; n - количество признаков; Hj - значимость j-гo признака: kij - качественная оценка j-гo признака для i-го объекта. [3]

Использование данной формулы позволяет варьировать качественные показатели в зависимости от типа образовательного учреждения, а также задач оценки качества образования. Таким образом, оценка качества образования подразумевает введение количественной характеристики показателей образовательного процесса, которая характеризует выбранную стратегию управления как хорошую или плохую. Данные показатели, определяющие качество деятельности образовательного учреждения математически представляют собой функцию векторов текущего состояния процесса и управляющего воздействия. Математические оценки позволяют объектив оценить анализируемый показатель.

Список использованной литературы:

1. Васильев В.Н. и др. О математических моделях оптимального управления системы подготовки специалистов. – Петрозаводск: Изд-во Петр. ГУ, 1997. – 267с. – С.145.

2. Федюкин В.К. Методы оценки и управления качеством промышленной продукции. – М.: Знание, 2000. – 364с. – С.143.

3. Черницкий В.И. Математическое моделирование динамических систем. – Петрозаводск: Изд-во Петр. ГУ, 1996. – 348с. – С.266.