Индексный анализ

Общее понятие об индексах и индексном методе

В практике статистики индексы наряду со средними величинами являются наиболее распространенными статистическими показателями. С их помощью характеризуется развитие национальной экономики в целом и ее отдельных отраслей, исследуется роль отдельных факторов в формировании важнейших экономических показателей, индексы используются также в международных сопоставлениях экономических показателей, определении уровня жизни, мониторинге деловой активности в экономике и т. д.

Индекс (лат. index) – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Различия условий может проявляться во времени (индексы динамики), в пространстве (территориальные индексы) и в выборе в качестве базы сравнения какого-либо условного уровня.

По охвату элементов совокупности (ее объектов, единиц и их признаков) различают индексы индивидуальные (элементарные) и сводные (сложные), которые в свою очередь делятся на общие и групповые.

Индивидуальные индексы – это результат сравнения двух показателей, относящихся к одному объекту, например сравнение цен какого-либо товара, объема его реализации и т. д. В статистико-экономическом анализе деятельности предприятий и отраслей широко применяются индивидуальные индексы качественных и количественных показателей. На-

пример, индекс цен ip = P1 / P0 характеризует относительное изменение уровня цены единицы каждого вида продукции в отчетном периоде по сравнению с базисным и является качественным показателем.

Индекс физического объема iq = q1 / q2 показывает, во сколько раз изменилось производство данного вида продукции в отчетном периоде по отношению к периоду, с которым проводилось сравнение, и является количественным показателем.

Сводный индекс характеризует соотношение уровней нескольких элементов совокупности (например, изменение объема выпуска нескольких видов продукции, имеющих различную натурально-вещественную форму, или изменение уровня производительности труда при производстве нескольких видов продукции). Если изучаемая совокупность состоит из нескольких групп, то сводные индексы, каждый из которых характеризует изменение уровней отдельной группы единиц, являются групповы1ми (субиндексами), а сводный индекс, охватывающий всю совокупность единиц, – общим (тотальным) индексом. Сводные индексы выражают соотношение сложных социально-экономических явлений и состоят из двух частей: индексируемой величины и соизмерителя, который называется весом.

Показатель, изменение которого характеризует индекс, называется индексируемым. Индексируемые показатели могут быть двоякого рода. Одни из них измеряют общий, суммарный размер (объем) того или иного явления и условно называются объемными, экстенсивными (физический объем продукции данного вида, численность работников, общие затраты труда на производство продукции, общая себестоимость продукции и т. п.). Эти показатели получаются как итог непосредственного подсчета или суммирования и являются исходными, первичными.

Другие показатели измеряют уровень явления или признака в расчете на ту или иную единицу совокупности и условно называются качественныжи, интенсивныши: выработка продукции в единицу времени (или на одного работника), затраты рабочего времени на единицу продукции, себестоимость единицы продукции и т. д. Эти показатели получаются путем деления объемных показателей, т. е. носят расчетный, вторичный характер. Они измеряют интенсивность, эффективность явления или процесса и, как правило, являются либо средними, либо относительными величинами.

При использовании индексного метода применяется определенная символика, т. е. система условных обозначений. Каждый индексируемый показатель обозначается определенной буквой (обычно латинской). Введем следующие условные обозначения:

Q – количество (объем) произведенной продукции (или количество проданного товара) данного вида в натуральном выражении;

Т – общие затраты рабочего времени (труда) на производство продукции данного вида, измеряемые в человеко-часах или человеко-днях; в некоторых случаях этой же буквой обозначается среднее списочное число работников;

z – себестоимость единицы продукции;

t – трудоемкость единицы продукции;

p – цена единицы продукции или товара;

– общий расход сырья, материала или топлива на производство продукции данного вида и объема.

Показатели за базисный период имеют в формулах подстрочный знак «0», а за сравниваемый (текущий, отчетный) период – знак «1». Индивидуальные индексы обозначаются буквой i и тоже снабжаются подстрочным знаком – обозначением индексируемого показателя. Так, iQ означает индивидуальный индекс количества (физического объема) произведенной продукции (или проданного товара) данного вида; iz – индивидуальный индекс себестоимости единицы продукции данного вида и т. п.

Сводные индексы обозначаются буквой I и также сопровождаются подстрочными значками показателей, изменение которых они характеризуют. Например, It – сводный индекс трудоемкости единицы продукции и т. д.

Индивидуальные индексы являются обычными относительными величинами, т. е. могут быть названы индексами только в широком понимании этого термина. Индексы в узком смысле, или собственно индексы, – это тоже показатели относительные, но особого рода. Они имеют более сложную методику построения и расчета, а специфические приемы их построения и составляют суть индексного метода.

Социально-экономические явления и характеризующие их показатели могут быть соизмеримыми, т. е. иметь общую меру, и несоизмеримыми. Так, объем продукции или товара одного и того же вида и сорта, произведенные на разных предприятиях или проданные в разных магазинах, соизмеримы и могут суммироваться, а объемы разных видов продукции или товаров несоизмеримы и непосредственно суммироваться не могут. Нельзя, например, складывать килограммы хлеба с литрами молока, метрами ткани и парами обуви. Несоизмеримость и невозможность непосредственного суммирования при построении и расчете сводного индекса объясняется здесь не столько различием натуральных единиц измерения, сколько различием потребительских свойств, неодинаковой натурально-вещественной формой этих продуктов или товаров.

В связи с этим для исчисления сводных индексов необходимо привести их составные части к сопоставимому виду. Единство различных видов продукции или разных товаров состоит в том, что они являются продуктами труда, имеют определенную стоимость и ее денежное выражение – цену (p). Каждый продукт имеет также ту или иную себестоимость (z) и трудоемкость (t). Эти качественные показатели и могут быть использованы в качестве общей меры – коэффициентов соизмерения разнородных продуктов. Умножая объем продукции каждого вида (Q) на соответствующую цену, себестоимость или трудоемкость единицы продукции, мы сведем различные продукты к одному и тому же единству и получим сравнимые показатели.

Аналогично обстоит дело и при построении сводных индексов качественных показателей. Пусть, например, нас интересует изменение общего уровня цен на различные проданные товары. Хотя формально цены разных товаров соизмеримы, однако непосредственное их суммирование без учета количества проданного товара каждого вида дает величину, лишенную самостоятельного практического значения. Поэтому сводный индекс цен нельзя построить как отношение простых сумм: ip = Σp1/Σp2. Цены отдельных товаров не учитывают конкретного количества проданных товаров и их статистического веса и роли в процессе товарооборота. Простые суммы цен отдельных товаров непригодны для построения сводного индекса еще и потому, что цены зависят от единицы измерения товаров, изменение которых даст другие суммы и другую величину индекса.

Следовательно, при построении сводных индексов качественных показателей их нельзя рассматривать в отрыве от связанных с ними объемных показателей, в расчете на единицу которых вычислены эти качественные показатели. Только умножив тот или иной качественный показатель (p, z, t) на непосредственно связанный с ними объемный показатель (Q), мы сможем учесть роль и статистический вес каждого вида продукции (или товара) в том или ином экономическом процессе – процессе образования общей стоимости (pQ), общей себестоимости (zQ), общих затрат рабочего времени (tQ) и т. п. Вместе с тем мы получим показатели, суммирование которых имеет практическую значимость.

Таким образом, первая особенность индексного метода и собственно индексов состоит в том, что индексируемый показатель рассматривается не изолированно, а во взаимосвязи с другими показателями.

Умножая индексируемый показатель на другой, связанный с ним, мы сводим различные явления к их единству, обеспечиваем их количественную сравнимость и учитываем их вес в реальном экономическом процессе. Поэтому показатели-сомножители, связанные с индексируемыми показателями, принято называть весами индексов, а умножение на них – взвешиванием.

Однако умножение значений индексируемого показателя на связанные с ними значения другого показателя (веса) еще не решает проблему собственно индекса. Умножив, например, цены на соответствующие им количества товаров, мы найдем стоимость этих товаров в каждом периоде и тем самым решим проблему соизмерения и взвешивания. Однако сопоставление полученных сумм произведений (Σp1Q1 и Σp0Q0) дает показатель, который характеризует изменение товарооборота, зависящего от двух факторов – цен и количества (объема) товаров, но не дает характеристику изменения уровня цен и уровня производства товаров:

Для того чтобы индекс охарактеризовал изменение только одного фактора, нужно устранить в формуле (7.1) изменение другого фактора, зафиксировав его как в числителе, так и в знаменателе на уровне одного и того же периода. Например, для оценки объема разнородной продукции в двух сравниваемых периодах нужно оценить товары, проданные в обоих периодах по одним и тем же, например базисным, ценам (р0). Полученный показатель отразит изменение только одного фактора – физического объема продукции Q:

А для оценки изменения уровня цен на группу товаров нужно сопоставлять одинаковые объемы этих товаров, т. е. количество товаров (Q) зафиксировать и в числителе, и в знаменателе индекса на одном и том же уровне (либо на базисном, либо на отчетном). Таким образом, построенные сводные индексы цен будут характеризовать только изменение цен, т. е. индексируемого показателя, так как изменение весов (Q) будет устранено (элиминировано) благодаря их фиксированию: Ip =Σp1q1/Σp0q1; Ip =Σp1q0/Σp0q0.

В обоих случаях (Iq и Ip) индекс отразил изменение только одного фактора – индексируемого показателя благодаря фиксированию другого (весов) на одном и том же уровне. Элиминирование влияния изменения весов путем их фиксирования в числителе и знаменателе индекса на одном и том же уровне – вторая особенность индексов и индексного метода.

Рассматривая проблемы, возникающие при построении собственно индексов, ставилась задача дать сравнительную характеристику уровней сложного явления, состоящего из разнородных элементов (разные виды продукции и т. п.). Так, Ip должен показать, как изменился в целом уровень цен, т. е. измерить динамику цен различных товаров в виде одного обобщающего показателя. Исторически собственно индексы появились как результат решения именно этой экономической задачи – задачи обобщения, синтеза динамики отдельных элементов сложного явления в одном обобщающем показателе, сводном индексе.

Однако собственно индексы используются для решения и другой задачи – анализа влияния изменения отдельных показателей-факторов на изменение показателя, представляющего функцию этих факторов-аргументов. Так, общая стоимость проданных товаров (товарооборот – Σpq) есть функция их цен (р) и количеств (объемов – Q), поэтому можно поставить задачу измерить влияние каждого из этих факторов на изменение товарооборота, т. е. определить, как он изменился отдельно за счет изменения каждого фактора. Индексы, применяемые для решения подобных аналитических задач, также строятся с использованием специфических особенностей индексного метода – взвешивания и элиминирования изменения весов.

Таким образом, собственно индекс – это относительный показатель особого рода, в котором уровни социально-экономического явления рассматриваются в связи с другим (или другими) явлением, изменение которого при этом элиминируется. Показатели, связанные с индексируемым показателем, используются в качестве весов индекса, а взвешивание и элиминирование изменения весов (фиксирование в числителе и знаменателе индекса на одном и том же уровне) составляют специфику собственно индексов и индексного метода.

Агрегатные индексы качественных показателей

Каждый качественный показатель связан с тем или иным объемным показателем, в расчете на единицу измерения которого он исчисляется (или к единице измерения которого относится). Так, цена единицы товара связана с его количеством (Q); с объемом произведенной продукции связаны такие качественные показатели, как цена (р), себестоимость (z) и трудоемкость (t = T / Q) единицы продукции, а также удельный расход сырья, материалов (m = M / Q).

Сводные индексы качественных показателей должны характеризовать не их изменение вообще применительно к какому-либо произвольному набору товаров или продукции, а изменение цен, себестоимости, трудоемкости или удельных расходов вполне определенного количества произведенной продукции или проданных товаров. Это и достигается путем взвешивания – умножения уровней индексируемого качественного показателя на значения связанного с ним объемного показателя (веса) – и фиксирования весов в числителе и знаменателе индекса на одном и том же уровне. Сопоставление сумм таких произведений дает агрегатный индекс. Аналогично могут быть построены агрегатные индексы динамики себестоимости и трудоемкости единицы продукции, а также индекс удельного расхода сырья или материала.

Основной проблемой при построении этих сводных индексов является экономически обоснованный выбор уровня, на котором нужно зафиксировать веса индекса, т. е. в данном случае объем продукции (или товаров) – Q.

Обычно перед сводным индексом динамики качественного показателя ставится задача измерить не только относительное изменение уровня, но и абсолютную величину того экономического эффекта, который получен в текущем периоде в результате этого изменения: сумму экономии покупателей за счет снижения цен (или сумму их дополнительных расходов, если цены повысились), сумму экономии (или дополнительных затрат) за счет изменения себестоимости и т. п.

Такая постановка задачи приводит к индексам динамики качественных показателей с весами текущего периода:

• во-первых, исследователя интересует изменение себестоимости или трудоемкости той продукции, которая выпущена в настоящее время, а не в прошлом;
• во-вторых, экономический эффект должен быть увязан с фактическими результатами текущего, отчетного, а не предыдущего (базисного) периода.

В качестве примера приведем агрегатный индекс себестоимости:

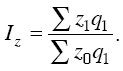
Таким образом, в этом индексе числитель представляет собой сумму фактических затрат на продукцию в отчетном периоде, а знаменатель – условную величину, которая показывает, сколько средств было бы затрачено на продукцию отчетного периода, если бы себестоимость единицы каждого вида продукции сохранялась на базисном уровне.

Реальный экономический эффект, полученный за счет изменения себестоимости единицы продукции, выражается абсолютной величиной, которая вычисляется как разность между суммами в числителе и знаменателе индекса: (Σz1q1 ?Σz0q1) или (Σ z1Σz0 q1).

Следовательно, взвешивание по весам отчетного (текущего) периода увязывает индекс качественного показателя с показателем экономического эффекта, который получен за счет изменения индексируемого показателя. Поэтому агрегатные индексы динамики качественный показателей строятся и вычисляются обычно с весами отчетного периода:

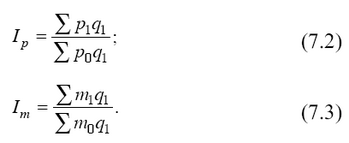
Формула (7.2) представляет собой сводный индекс цен, а формула (7.3) – расчет сводного индекса расхода материалов. В этих индексах разность между числителем и знаменателем характеризует в первом случае уменьшение либо увеличение затрат на приобретение одного и того же набора товаров в зависимости от знака разности; во втором случае – увеличение или уменьшение расхода материалов на производство одного и того же объема продукции.

Агрегатные индексы объемных показателей

Объемные показатели могут быть соизмеримыми (Т, рQ, zQ) и несоизмеримыми (объем продукции или товаров разного вида – Q). Соизмеримые объемные показатели могут непосредственно суммироваться, и построение агрегатных индексов не вызывает трудностей.

Для получения общего итога и построения агрегатного индекса несоизмеримого объемного показателя нужно предварительно соизмерить отдельные значения этого показателя. Исходя из экономической сущности явления, нужно найти общую меру и использовать ее в качестве коэффициента соизмерения. Такой общей мерой для объемных показателей являются связанные с ними качественные показатели. Так, объемы различных видов продукции могут быть соизмерены с помощью цены (р), себестоимости (z) и трудоемкости (t) этих продуктов. Умножая индексируемый объемный показатель на тот или иной качественный показатель, не только обеспечивается возможность суммирования, но одновременно учитывается также роль каждого элемента, например продукта, в реальном экономическом процессе, т. е. его статистический вес в этом процессе.

Поскольку в индексе объемного показателя в качестве весов могут выступать различные качественные показатели, возникает вопрос о том, какой же именно их них следует использовать. Этот вопрос в каждом конкретном случае должен решаться в соответствии с той познавательной экономической задачей, которая ставится перед индексом, т. е. выбор тех или иных весов-соизмерителей должен быть обоснован экономически.

В практике экономической и статистической работы в качестве весов агрегатного индекса объема продукции обычно используются цены. Так строятся индексы объема промышленной и сельскохозяйственной продукции, а также индексы физического объема товарооборота.

В ряде случаев изменение объема продукции интересует не само по себе, а с точки зрения его влияния на изменение показателя более сложного порядка: общей стоимости продукции, общей ее себестоимости, общих затрат рабочего времени, общего объема производства на данном его участке и т. п. В таких случаях выбор весов-соизмерителей определяется взаимосвязью показателей-факторов, от которых зависит более сложный показатель.

Чтобы индекс отражал только изменение индексируемого объемного показателя, веса в его числителе и знаменателе фиксируются на уровне одного и того же периода. В практике экономической работы в индексах динамики объемных показателей веса обычно фиксируются на уровне базисного периода (см. формулу 7.2). Это обеспечивает возможность построения систем взаимосвязанных индексов.

Для индивидуальных объемных показателей (объем реализации, объем производительности продукции, посевная площадь) веса выбираются на уровне базисного периода. Например:

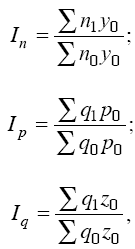
где In– сводный индекс урожайности; I – сводный индекс стоимости товарооборота; Iq – сводный индекс себестоимости.

В отличие от индексов качественных показателей, которые исчисляются по сравнимому кругу единиц (сравнимой продукции), сводные индексы объемных показателей в целях полноты и точности должны охватывать весь круг единиц, произведенных (или проданных) в каждом периоде. В связи с этим возникает вопрос о том, какие значения весов следует брать для тех видов продукции, которые в одном из сравниваемых периодов не производились.

В практике статистики в таких случаях применяются два способа. При расчете индексов объема промышленной продукции новые ее виды, для которых нет цен базисного периода, оцениваются условно по ценам текущего периода. При расчете же индексов объема проданных товаров используется метод, основанный на условном предположении, что и цены на новые товары изменились в той же степени, что цены на сравниваемый круг аналогичных товаров.

Ряды агрегатных индексов с постоянными и переменными весами

При изучении динамики экономических явлений строятся и исчисляются индексы за ряд последовательных периодов. Они образуют ряды либо базисных, либо цепных индексов. В ряду базисных индексов сравнение индексируемого показателя в каждом индексе производится с уровнем одного и того же периода, а в ряду цепных индексов индексируемый показатель сопоставляется с уровнем предыдущего периода.

В каждом отдельном индексе веса в его числителе и знаменателе обязательно фиксируются на одном и том же уровне. Если же строится ряд индексов, то веса в нем могут быть либо постоянными для всех индексов ряда, либо переменными.

Ряд базисных индексов объема продукции Σq1p0/Σq0p0,Σq2p0/Σq0p0,Σq3p0/Σq0p0 и т. д. имеет постоянные веса (р0). Постоянные веса (р0) имеет и ряд цепных индексов: Σq1p0/Σq0p0,Σq2p0/Σq1p0,Σq3p0/Σq2p0 и т. д.

Ряд цепных индексов цен Σp1q1/Σp1q0,Σp2q2/Σp2q0, Σp3q3 /Σp3q2 и т. д. построен с переменными весами (в 1-м индексе – q1 во 2-м – q2 и т. д.).

Для индексов динамики с постоянными весами имеет силу взаимосвязь между цепными и базисными темпами роста (индексами):

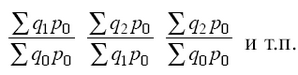
Таким образом, использование постоянных весов в течение ряда лет позволяет переходить от цепных индексов к базисным, и наоборот. Поэтому ряды индексов объема продукции и объема проданных товаров строятся в статистической практике с постоянными весами. Так, в индексах объема продукции в качестве постоянных весов используются цены, зафиксированные на уровне, который был установлен на 1 января какого-либо базисного года. Такие цены, используемые в течение ряда лет, называются сопоставимыми (фиксированными).

Использование в индексах объема продукции (товаров) сопоставимых цен позволяет путем простого суммирования получать итоги за несколько лет. Сопоставимые цены не должны сильно отличаться от действующих (текущих) цен, поэтому их периодически пересматривают, переходя к новым сопоставимым ценам. Чтобы иметь возможность исчислять индексы объема продукции за длительные периоды, в течение которых применялись различные сопоставимые цены, продукцию одного года оценивают как в прежних, так и в новых фиксированных ценах. Индекс за длительный период исчисляют цепным методом, т. е. путем перемножения индексов за отдельные отрезки этого периода.

Ряды индексов качественных показателей, которые экономически правильно взвешивать по весам текущего периода, строятся с переменными весами.

Построение сводных территориальных индексов

При построении территориальных индексов, т. е. при сравнении показателей в пространстве (межрайонные, сравнение между разными предприятиями и др.), возникают вопросы о выборе базы сравнения и района (объекта), на уровне которого следует зафиксировать веса индекса. В каждом конкретном случае эти вопросы нужно решать исходя из задач исследования. Выбор базы сравнения зависит, в частности, от того, будут ли сравнения двусторонними (например, сравнение показателей двух соседних территориальных единиц) или многосторонними (сравнение показателей нескольких территорий, объектов).

При двусторонних сравнениях каждая территория или объект с одинаковым основанием может быть принят как в качестве сравниваемого, так и в качестве базы сравнения. В связи с этим возникает вопрос о фиксировании весов сводного индекса на уровне того или иного района (объекта). Пусть, например, нужно определить, в какой из двух областей и насколько процентов ниже себестоимость единицы продукции и больше объем ее производства.

Если сравнивать область А с областью Б, достаточно обоснованный и простой путь состоит в том, чтобы зафиксировать в индексе себестоимости в качестве весов объемы продукции в целом по обеим территориям (Q = QA + QБ), тогда получим: Iz =Σzq/Σzq.

При многосторонних сравнениях, например при сравнениях качественных показателей по нескольким областям, нужно, соответственно, расширить и границы территории, на уровне которой фиксируются веса.

В сводных территориальных индексах объемных показателей в качестве весов могут быть приняты средние уровни соответствующих качественных показателей, вычисленные в целом по сравниваемым территориям. Так, в нашем примере

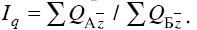
Средние индексы

В зависимости от методологии расчета индивидуальных и сводных индексов различают средние арифметические и средние гармонические индексы. Другими словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего арифметического или гармонического индекса, т. е. он может быть преобразован в средний арифметический и средний гармонический индексы.

Идея построения сводного индекса в виде средней величины из индивидуальных (групповых) индексов вполне объяснима: ведь сводный индекс является общей мерой, характеризующей среднюю величину изменения индексируемого показателя, и, конечно, его величина должна зависеть от величин индивидуальных индексов. А критерием правильности построения сводного индекса в форме средней величины (среднего индекса) является его тождественность агрегатному индексу.

Преобразование агрегатного индекса в средний из индивидуальных (групповых) индексов производится следующим образом: либо в числителе, либо в знаменателе агрегатного индекса индексируемый показатель заменяется его выражением через соответствующий индивидуальный индекс. Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический, если же в знаменателе – то в средний гармонический из индивидуальных индексов.

Например, известен индивидуальный индекс физического объема iq = q1/q0 и стоимость продукции каждого вида в базисном периоде (q0p0). Исходной базой построения среднего из индивидуальных индексов служит сводный индекс физического объема:

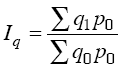
(агрегатная форма индекса Ласпейреса).

Из имеющихся данных непосредственно суммированием можно получить только знаменатель формулы. Числитель же может быть получен перемножением стоимости отдельного вида продукции базисного периода на индивидуальный индекс:

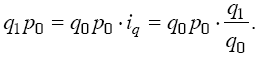
Тогда формула сводного индекса примет вид:

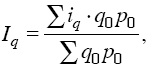
т. е. получим средний арифметический индекс физического объема, где весами служит стоимость отдельных видов продукции в базисном периоде.

Допустим, что в наличии имеется информация о динамике объема выпуска каждого вида продукции (q) и стоимости каждого вида продукции в отчетном периоде (p1q1). Для определения общего изменения выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше:

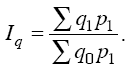
Числитель формулы можно получить суммированием величин q1P1, а знаменатель – делением фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, т. е. делением: p1q1/iq, тогда:

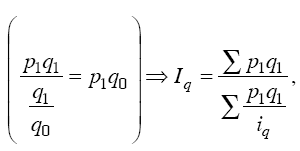
таким образом, получаем формулу среднего взвешенного гармонического индекса физического объема.

Применение той или иной формулы индекса физического объема (агрегатного, среднего арифметического и среднего гармонического) зависит от имеющейся в распоряжении информации. Также нужно иметь в виду, что агрегатный индекс может быть преобразован и рассчитан как средний из индивидуальных индексов только при совпадении перечня видов продукции или товаров (их ассортимента) в отчетном и базисном периодах, т. е. когда агрегатный индекс построен по сравнимому кругу единиц (агрегатные индексы качественных показателей и агрегатные индексы объемных показателей при условии сравнимого ассортимента).