Статистика процентных ставок. Простые и сложные проценты - Экономическая статистика (Яковлева А.В.)

Статистика процентных ставок является составной частью статистики финансов. Базисным понятием статистики процентных ставок являются процентные деньги или проценты.

Процентные деньги – это абсолютная величина дохода от предоставленных в долг финансовых ресурсов (выдача ссуды, предоставление банковского кредита, учет векселя, помещения денег на депозитный счет и т. д.).

При заключении договора о выдаче денег в долг кредитор и должник договариваются о размере процентной ставки.

Процентная ставка представляет собой отношение абсолютной суммы процентных денег, выплачиваемых в единицу времени, к величине ссуды. Процентная ставка чаще всего выражается в процентах.

Также при заключении договора о выдаче денег в долг определяется период действия данного договора (несколько лет, месяц, неделя, день и т. д.) и периодичность начисления процентов. Временной интервал, в конце которого начисляется процентная ставка, называется периодом начисления (год, полугодие, квартал, месяц, день). На практике процентная ставка указывается в процентах годовых.

Проценты могут выплачиваться либо по мере их начисления, либо присоединяться к основной сумме долга (капитализация процентов). Увеличение начальной суммы денег в результате начисления процентов называется наращиванием этой суммы.

Процентные ставки классифицируются по ряду признаков.

По методу начисления процентов различают:

1. процентные ставки;
2. учетные ставки.

Процентные ставки используются в том случае, если базой для начисления процентов является первоначальная стоимость займа, и начисленные проценты присоединяются к этой сумме в конце отдельных периодов начисления или срока займа в целом (например, начисление процентов за кредит, на счет в банке и т. д.). Проценты, полученные по процентной ставке (ставке наращения), называются также декурсивными.

Если начисление процентов базируется на сумме, которая уплачивается должником, то в этом случае применяется учетная ставка, и проценты удерживаются при выдаче ссуды. Проценты, полученные по учетной ставке, называются также антисипативными.

Обозначим процентную ставку i. Тогда процентные деньги J за полученную ссуду будут рассчитываться на основе размера ссуды Р, процентной ставки i и времени пользования ссудой n, которое измеряется в годах (долях года).

Если база для начисления процентов является постоянной в течение всего времени пользования ссудой, то при расчетах процентных денег используются простые проценты:

J1=P * i – за первый год;

J2 = J1 + P * i = P * i * 2 – за второй год;

...

Jn = Jn-1 + P * i = P * i * n – за n лет.

В этом случае сумма, которую обязан заплатить должник с наращенными за весь период процентами, т. е. наращенная сумма долга S, определяется по формуле простых процентов:

S = P * (1 + in).

При сроке пользования ссудой менее одного года:

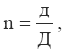
где д – это число дней ссуды;

Д – число дней в году (360, 365, 366).

Чаще всего простые проценты применяются при заключении сделок сроком до одного года.

Если база для начисления процентов периодически меняется в связи с присоединением суммы начисленных процентов к первоначальной сумме долга в течение пользования ссудой, то при расчетах используются сложные проценты:

За первый год: S1 = P + P * i = P * (1 + i);

за два года: S2 = S1 * (1 + i) = P * (1 + i) * (1 + i) = P * (1 + i)2;

...

за n лет: Sn = P * (1 + i)n.

Последняя формула называется формулой сложных процентов.

Сложные проценты применяются при долгосрочных финансовых операциях сроком более 1, 3, 5 и т. д. лет.

При использовании сложных процентов процентная сумма J за период n лет рассчитывается по формуле:

J = S – P = P * [(1 + i)n – 1].