Определение оптимального размера заказа

Оптимальный размер партии поставляемых товаров и, соответственно, оптимальная частота завоза зависят от следующих факторов: объем спроса (оборота); транспортно-заготовительные расходы; расходы на хранение запаса. В качестве критерия оптимальности выбирают минимум суммы расходов транспортно-заготовительных и на хранение. Транспортно-заготовительные расходы при увеличении размера заказа уменьшаются, так как закупки и перевозки товаров осуществляются более крупными партиями и, следовательно, реже. Расходы по хранению растут прямо пропорционально размеру заказа.

Для решения данной задачи необходимо минимизировать функцию, представляющую сумму расходов транспортно-заготовительных и на хранение, т. е. определить условия, при которых

С_общ = С_хран + С_трансп,

где С_общ – общие затраты на транспортировку и хранение; С_хран – затраты на хранение запаса; С_тсп – транспортно-заготовительные расходы.

Предположим, что за определенный период времени величина оборота составляет Q. Размер одной заказываемой партии S. Допустим, что новая партия завозится после того, как предыдущая полностью закончилась. Тогда средняя величина запаса составит S/2. Введем размер тарифа (М) за хранение товара. Он измеряется долей, которую составляют издержки по хранению за период Т в стоимости среднего запаса за тот же период.

Стоимость хранения товаров за период Т можно рассчитать по следующей формуле:

С_хран = М (S/2).

Размер транспортно-заготовительных расходов за период Т определится по формуле

С_хран = K(Q/S)

где К – транспортно-заготовительные расходы, связанные с размещением и доставкой одного заказа; Q/S – количество заказов за период времени. Подставив данные в основную функцию, получим Со₆щ = М (S/2) + K (Q/S).

Минимум С_общ имеется в точке, в которой ее первая производная по S равна нулю, а вторая производная больше нуля.

Найдем первую производную:

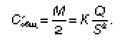
Найдем значение S, обращающее производную целевой функции в нуль:

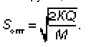
Полученная формула, позволяющая рассчитать оптимальный размер заказа, в теории управления запасами известна как формула Уилсона.