Методический инструментарий финансовых вычислений
Концепция и методический инструментарий оценки стоимости денег во времени
Финансовый менеджмент требует постоянного осуществления различного рода финансово-экономических расчетов, связанных с потоками денежных средств в разные периоды времени. Ключевую роль в этих расчетах играет оценка стоимости денег во времени.
Концепция стоимости денег во времени состоит в том, что стоимость денег с течением времени изменяется с учетом нормы прибыли на финансовом рынке, в качестве которой обычно выступает норма ссудного процента (или процента). Иными словами, в соответствии с этой концепцией одна и та же сумма денег в разные периоды времени имеет разную стоимость; эта стоимость в настоящее время всегда выше, чем в любом будущем периоде.
Концепция стоимости денег во времени играет основополагающую роль в практике финансовых вычислений. Она предопределяет необходимость учета фактора времени в процессе осуществления любых долгосрочных финансовых операций путем оценки и сравнения стоимости денег при начале финансирования со стоимостью денег при их возврате в виде будущей прибыли, амортизационных отчислений, основной суммы долга и т.д.
В процессе сравнения стоимости денежных средств при планировании их потоков в продолжительном периоде времени используется два основных понятия — будущая стоимость денег или их настоящая стоимость.
Будущая стоимость денег представляет собой сумму инвестированных в настоящий момент средств, в которую они превратятся через определенный период времени с учетом определенной ставки процента (процентной ставки). Определение будущей стоимости денег характеризует процесс наращения их стоимости (компаундинг), который состоит в присоединении к их первоначальной сумме начисленной суммы процентов.
Настоящая стоимость денег представляет собой сумму будущих денежных средств, приведенной с учетом определенной ставки процента к настоящему периоду времени. Определение настоящей стоимости денег характеризует процесс дисконтирования их стоимости, который представляет операцию, обратную наращению, осуществляемую путем изъятия из будущей стоимости соответствующей суммы процентов (дисконтной суммы или "дисконта").
При проведении финансовых вычислений, связанных с оценкой стоимости денег во времени, процессы наращения или дисконтирования стоимости могут осуществляться как по простым, так и по сложным процентам.
Простой процент представляет собой сумму дохода, начисляемого к основной сумме денежного капитала в каждом интервале общего периода его использования, по которой дальнейшие ее перерасчеты не осуществляются. Начисление простого процента применяется, как правило, при краткосрочных финансовых операциях.
Сложный процент представляет собой сумму дохода, начисляемого в каждом интервале общего периода его использования, которая не выплачивается, а присоединяется к основной сумме денежного интервала и в последующем платежном интервале сама приносит доход. Начисление сложного процента применяется, как правило, при долгосрочных финансовых операциях (инвестировании, кредитовании и т.п.).
Расчеты суммы процента могут осуществляться как в начале, так и в конце каждого интервала общего периода времени. В соответствии с этим, методы начисления процента разделяют на предварительный и последующий.
Предварительный метод начисления процента (метод пренумерандо или антисипативный метод) характеризует способ расчета платежей, при котором начисление процента осуществляется в начале каждого интервала.
Последующий метод начисления процента (метод постнумерандо или декурсивный метод) характеризует способ платежей, при котором начисление процента осуществляется в конце каждого интервала.
Платежи, связанные с выплатой суммы процента и возвратом основной суммы долга представляют собой один из видов денежного потока, подразделяемый на дискретный и непрерывный.
Дискретный денежный поток характеризует поток платежей на вложенный денежный капитал, который имеет четко детерминированный период начисления процентов и конечный срок возврата основной его суммы.
Непрерывный денежный поток характеризует поток платежей на вложенный денежный капитал, период начисления процентов по которому не ограничен, а соответственно не определен и конечный срок возврата основной его суммы. Одним из наиболее распростаренных видов непрерывного денежного потока является аннуитет (финансовая рента) — длительный поток платежей, характеризующийся одинаковым уровнем процентных ставок в каждом из интервалов рассматриваемого периода времени.
Основным инструментом оценки стоимости денег во времени выступает процентная ставка (ставка процента) — удельный показатель, в соответствии с которым в установленные сроки выплачивается сумма процента в расчете на единицу денежного капитала. Обычно процентная ставка характеризует соотношение годовой суммы процента и суммы предоставленного (заимствованного) денежного капитала (выраженное в десятичной дроби или в процентах). Это понятие отличается многообразием конкретных его видов, используемых в практике финансовых вычислений. Процентная ставка, используемая в процессе наращения или дисконтирования стоимости денежных средств (оценки их будущей и настоящей стоимости), классифицируется по следующим основным признакам (рис. 3.1).
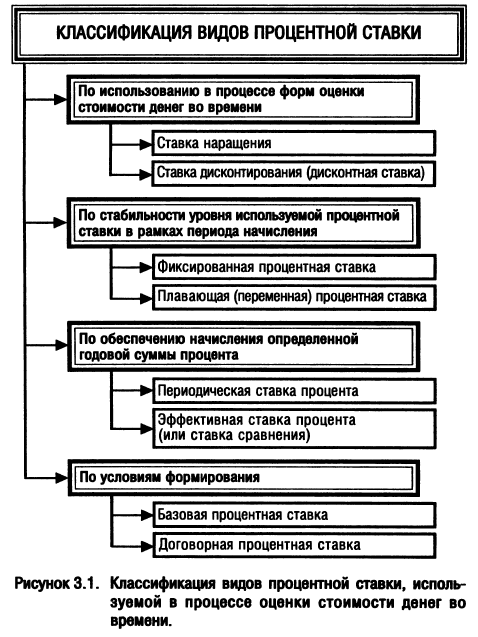
1. По использованию в процессе форм оценки стоимости денег во времени различают ставку наращения и ставку дисконтирования (дисконтную ставку).
Ставка наращения представляет собой процентную ставку, по которой осуществляется процесс наращения стоимости денежных средств (компаундинг), т.е. определяется их будущая стоимость.
Ставка дисконтирования (дисконтная ставка) представляет собой процентную ставку, по которой осуществляется процесс дисконтирования стоимости денежных средств, т.е. определяется их настоящая стоимость.
2. По стабильности уровня используемой процентной ставки в рамках периода начисления выделяют фиксированную и плавающую процентные ставки.
Фиксированная ставка характеризуется неизменным ее уровнем на протяжении всех интервалов общего периода начисления.
Плавающая (или переменная) процентная ставка характеризуется регулярно пересматриваемым ее уровнем по соглашению сторон в разрезе отдельных интервалов общего периода начислений. Такой пересмотр обусловливается изменением средней нормы процента на финансовом рынке (или в отдельных его сегментах), изменением темпа инфляции и другими условиями.
3. По обеспечению начисления определенной годовой суммы процента различают периодическую и эффективную процентные ставки.
Периодическая ставка процента при обеспечении определенной годовой суммы процента может варьировать как по уровню, так и по продолжительности отдельных интервалов на протяжении годового периода платежей.
Эффективная ставка процента (или ставка сравнения) характеризует среднегодовой ее уровень, определяемый отношением годовой суммы процента, начисленного по периодическим его ставкам, к основной сумме капитала.
4. По условиям формирования различают базовую и договорную процентные ставки.
Базовая процентная ставка характеризуется определенным исходным ее уровнем в качестве первоначальной основы последующей ее конкретизации кредитором (заемщиком) в зависимости от условий осуществления соответствующей финансовой операции.
Договорная процентная ставка характеризует конкретизированный ее уровень, согласованный кредитором и заемщиком и отраженный в соответствующем кредитном (депозитном, инвестиционном) договоре.
Система основных базовых понятий позволяет последовательно рассмотреть методический инструментарий оценки стоимости денег во времени в разрезе наиболее характерных вариантов осуществления такой оценки. Этот методический инструментарий дифференцируется в разрезе следующих видов вычислений (рис. 3.2).
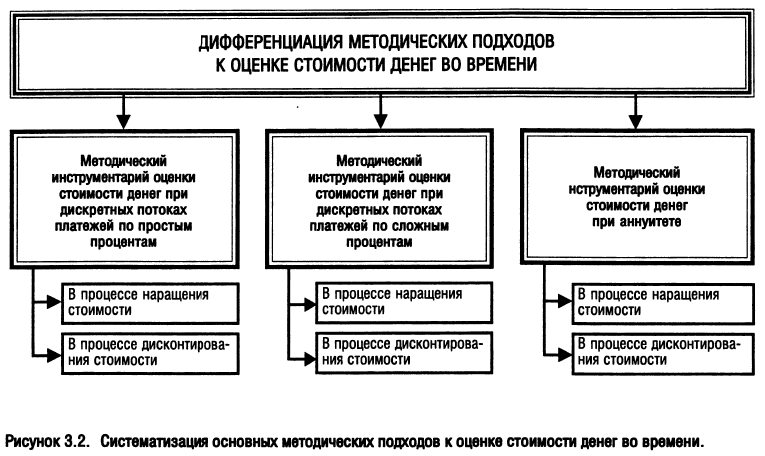
I. Методический инструментарий оценки стоимости денег по простым процентам использует наиболее упрощенную систему расчетных алгоритмов.
1. При расчете суммы простого процента в процессе наращения стоимости (компаундинга) используется следующая формула:
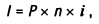
где I — сумма процента за обусловленный период времени в целом;
Р — первоначальная сумма (стоимость) денежных средств;
n — количество интервалов, по которым осуществляется расчет процентных платежей, в общем обусловленном периоде времени;
i — используемая процентная ставка, выраженная десятичной дробью.
В этом случае будущая стоимость вклада (S) с учетом начисленной суммы процента определяется по формуле:
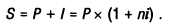
Пример: Необходимо определить сумму простого процента за год при следующих условиях: первоначальная сумма вклада — 1000 усл. ден. eд.; процентная ставка, выплачиваемая ежеквартально —20%.
Подставляя эти значения в формулу, получим сумму процента:
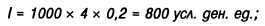
будущая стоимость вклада в этом случае составит:
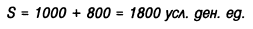
Множитель (1 + ni) называется множителем (или коэффициентом) наращения суммы простых процентов. Его значение всегда должно быть больше единицы.
Процесс наращения суммы вклада во времени по простым процентам может быть представлен графически (рис. 3.3).
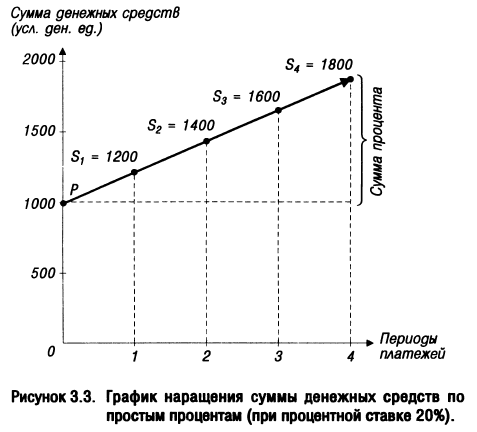
2. При расчете суммы простого процента в процессе дисконтирования стоимости (т.е. суммы дисконта) используется следующая формула:
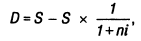
где D — сумма дисконта (рассчитанная по простым процентам) за обусловленный период времени в целом;
S — стоимость денежных средств;
n — количество интервалов, по которым осуществляется расчет процентных платежей, в общем обусловленном периоде времени;
i — используемая дисконтная ставка, выраженная десятичной дробью.
В этом случае настоящая стоимость денежных средств (F) с учетом рассчитанной суммы дисконта определяется по следующим формулам:
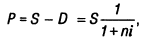
Пример: Необходимо определить сумму дисконта по простому проценту за год при следующих условиях: конечная сумма вклада определена в размере 1000 усл. ден. eд.; дисконтная ставка составляет 20% в квартал.
Подставляя эти значения в формулу расчета суммы дисконта, получим:
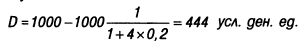
Соответственно настоящая стоимость вклада, необходимого для получения через год 1000 усл. ден. единиц, должна составить:
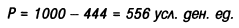
Используемый в обеих случаях множитель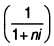 
называется
дисконтным множителем (коэффициентом) суммы простых процентов, значение которого всегда должно быть меньше единицы.
Процесс дисконтирования суммы денежных средств может быть представлен графически (рис. 3.4).
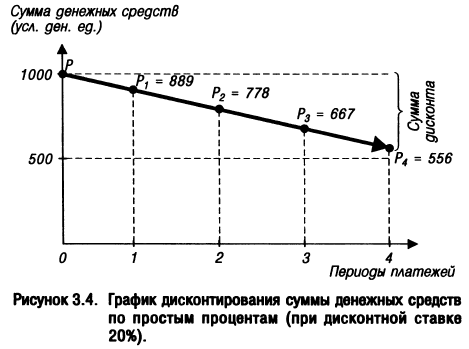
II. Методический инструментарий оценки стоимости денег по сложным процентам использует более обширную и более усложненную систему расчетных алгоритмов.
1. При расчете будущей суммы вклада (стоимости денежных средств) в процессе его наращения по сложным процентам используется следующая формула:
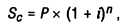
где Sc — будущая стоимость вклада (денежных средств) при его наращении по сложным процентам;
Р — первоначальная сумма вклада;
i — используемая процентная ставка, выраженная десятичной дробью;
n — количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.
Соответственно сумма процента (Iс) в этом случае определяется по формуле:
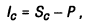
Графически процесс наращения стоимости вклада по сложным процентам представлен на рисунке 3.5.
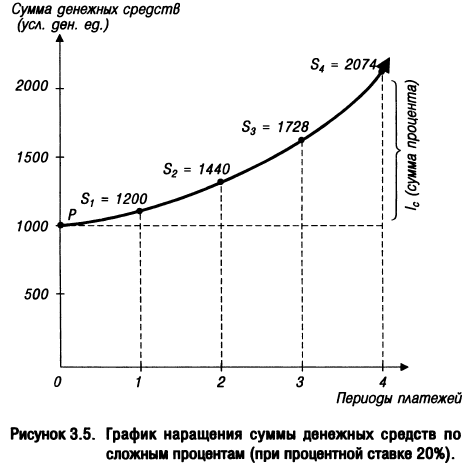
2. При расчете настоящей стоимости денежных средств в процессе дисконтирования по сложным процентам используется следующая формула:
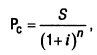
где Рс — первоначальная сумма вклада;
S — будущая стоимость вклада при его наращении, обусловленная условиями инвестирования;
i — используемая дисконтная ставка, выраженная десятичной дробью;
n — количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.
Соответственно сумма дисконта (Dc) в этом случае определяется по формуле:
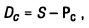
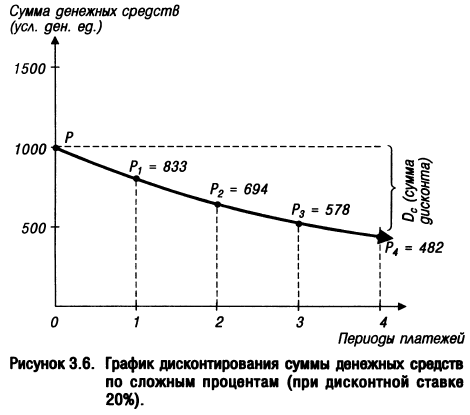
Графически процесс дисконтирования денежных средств по сложным процентам представлен на рис. 3.6.
3. При определении средней процентной ставки, используемой в расчетах стоимости денежных средств по сложным процентам, применяется следующая формула:
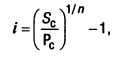
где i — средняя процентная ставка, используемая в расчетах стоимости денежных средств по сложным процентам, выраженная десятичной дробью;
Sc — будущая стоимость денежных средств;
Рс — настоящая стоимость денежных средств;
n — количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.
4. Длительность общего периода платежей, выраженная количеством его интервалов, в расчетах стоимости денежных средств по сложным процентам определяется путем логарифмирования по следующей формуле:
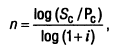
где Sc — будущая стоимость денежных средств;
Рс — настоящая стоимость денежных средств;
i — используемая процентная ставка, выраженная десятичной
5. Определение эффективной процентной ставки в процессе наращения стоимости денежных средств по сложным процентам осуществляется по формуле:
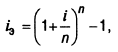
где iэ — эффективная среднегодовая процентная стака при наращении стоимости денежных средств по сложным процентам, выраженная десятичной дробью;
i — периодическая процентная ставка, используемая при наращении стоимости денежных средств по сложным процентам, выраженная десятичной дробью;
n — количество интервалов, по которым осуществляется каждый процентный платеж по периодической процентной ставке на протяжении года.
При оценке стоимости денег во времени по сложным процентам необходимо иметь в виду, что на результат оценки оказывает большое влияние не только используемая ставка процента, но и число интервалов выплат в течение одного и того же общего платежного периода. Иногда оказывается более выгодным инвестировать деньги под меньшую ставку процента, но с большим числом интервалов в течение предусмотренного периода платежа.
Используемые в процессе оценки стоимости денег множител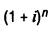и
и
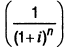называются соответственно множителем наращения и множителем дисконтирования суммы сложных процентов. Они положены в основу специальных таблиц финансовых вычислений, с помощью которых при заданных размерах ставки процента и количества платежных интервалов можно легко вычислить настоящую или будущую стоимость денежных средств по сложным процентам.
III. Методический инструментарий оценки стоимости денег при аннуитете связан с использованием наиболее сложных алгоритмов и определением метода начисления процента — предварительным (пре-нумерандо) или последующим (постнумерандо).
1. При расчете будущей стоимости аннуитета на условиях предварительных платежей (пренумерандо) используется следующая формула:
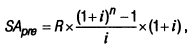
где SApre — будущая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо);
R — член аннуитета, характеризующий размер отдельного платежа;
i — используемая процентная ставка, выраженная десятичной дробью;
n — количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.
2. При расчете будущей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), применяется следующая формула:
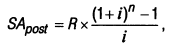
где SApost — будущая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо);
R — член аннуитета, характеризующий размер отдельного платежа;
i — используемая процентная ставка, выраженная десятичной дробью;
n — количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.
3. При расчете настоящей стоимости аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), используется следующая формула:
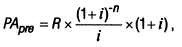
где РАрrе — настоящая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо);
R — член аннуитета, характеризующий размер отдельного платежа;
i — используемая процентная (дисконтная) ставка, выраженная десятичной дробью;
n — количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.
4. При расчете настоящей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), применяется следующая формула:
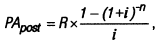
где PApost — настоящая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо);
R — член аннуитета, характеризующий размер отдельного платежа;
i — используемая процентная (дисконтная) ставка, выраженная десятичной дробью;
n — количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.
5. При расчете размера отдельного платежа при заданной будущей стоимости аннуитета используется следующая формула:
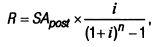
где R — размер отдельного платежа по аннуитету (член аннуитета при предопределенной будущей его стоимости);
SApost — будущая стоимость аннуитета (осуществляемого на условиях последующих платежей);
i — используемая процентная ставка, выраженная десятичной дробью;
n — количество интервалов, по которым намечается осуществлять каждый платеж, в обусловленном периоде времени.
6. При расчете размера отдельного платежа при заданной текущей стоимости аннуитета используется такая формула:
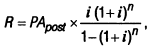
где R — размер отдельного платежа по аннуитету (член аннуитета при известной текущей его стоимости);
PApost — настоящая стоимость аннуитета (осуществляемого на условиях последующих платежей);
i — используемая процентная ставка, выраженная десятичной дробью;
n — количество интервалов, по которым намечается осуществлять каждый платеж, в обусловленном периоде времени.
В процессе расчета аннуитета возможно использование упрощенных формул, основу которых составляет только член аннуитета (размер отдельного платежа) и соответствующий стандартный множитель (коэффициент) его наращения или дисконтирования.
В этом случае формула для определения будущей стоимости аннуитета (осуществляемого на условиях последующих платежей), имеет вид:
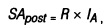
где SApost — будущая стоимость аннуитета (осуществляемого на условиях последующих платежей);
R — член аннуитета, характеризующий размер отдельного платежа;
IА — множитель наращения стоимости аннуитета, определяемый по специальным таблицам, с учетом принятой процентной ставки и количества интервалов в периоде платежей.
Соответственно, формула для определения настоящей стоимости аннуитета имеет вид:
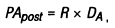
где PApost — настоящая стоимость аннуитета (осуществляемого на условиях последующих платежей);
R — член аннуитета, характеризующий размер отдельного платежа;
DА — дисконтный множитель аннуитета, определяемый по специальным таблицам, с учетом принятой процентной (дисконтной) ставки и количества интервалов в периоде платежей.
Использование стандартных множителей (коэффициентов) наращения и дисконтирования стоимости существенно ускоряет и облегчает процесс оценки стоимости денег во времени.
Концепция и методический инструментарий оценки фактора инфляции
В финансовом менеджменте постоянно приходится считаться с фактором инфляции, которая с течением времени обесценивает стоимость находящихся в обращении денежных средств.
Влияние инфляции сказывается на многих аспектах финансовой деятельности предприятия. В процессе инфляции происходит относительное занижение стоимости отдельных материальных активов, используемых предприятием (основных средств, запасов товарно-материальных ценностей и т.п.); снижение реальной стоимости денежных и других финансовых его активов (дебиторской задолженности, нераспределенной прибыли, инструментов финансового инвестирования и т.п.); занижение себестоимости производства продукции, вызывающее искусственный рост суммы прибыли и приводящее к росту налоговых отчислений с нее; падение реального уровня предстоящих доходов предприятия и т.п. Особенно сильно фактор инфляции сказывается на проведении долгосрочных финансовых операций предприятия.
Инфляция является объективным, постоянно действующим фактором, присущим развитию экономики не только нашей страны, но практически всех стран мирового сообщества. Даже в странах с развитой и наиболее устойчивой экономикой — США, Японии, ФРГ, Великобритании, франции и других — инфляционные процессы происходят непрерывно, хотя их интенсивность относительно низкая. В современной экономической теории принято даже считать, что рост уровня цен в пределах 10% в год является нормальным экономическим явлением, оказывающим стимулирующее воздействие на развитие производства.
Стабильность проявления фактора инфляции и его активное воздействие на результаты финансовой деятельности предприятия определяют необходимость постоянного учета влияния этого фактора в процессе финансового менеджмента.
Концепция учета влияния фактора инфляции в управлении различными аспектами финансовой деятельности предприятия заключается в необходимости реального отражения стоимости его активов и денежных потоков, а также в обеспечении возмещения потерь доходов, вызываемых инфляционными процессами, при осуществлении различных финансовых операций.
Для оценки интенсивности инфляционных процессов в стране используются два основных показателя, учитывающих фактор инфляции в финансовых вычислениях — темп и индекс инфляции.
Темп инфляции характеризует показатель, отражающий размер обесценения (снижения покупательной способности) денег в определенном периоде, выраженный приростом среднего уровня цен в процентах к их номиналу на начало периода.
Индекс инфляции характеризует показатель, отражающий общий рост уровня цен в рассматриваемом периоде, определяемый путем суммирования базового их уровня на начало периода (принимаемого за единицу) и темпа инфляции в этом же периоде (выраженного десятичной дробью).
При расчетах, связанных с корректировкой стоимости денег с учетом фактора инфляции принято использовать два понятия — номинальная и реальная сумма денежных средств.
Номинальная сумма денежных средств отражает оценку размеров денежных активов в соответствующих денежных единицах без учета изменения покупательной стоимости денег в рассматриваемом периоде.
Реальная сумма денежных средств отражает оценку размеров денежных активов с учетом изменения уровня покупательной стоимости денег в рассматриваемом периоде, вызванного инфляцией.
Для расчета этих сумм денежных средств в процессе наращения или дисконтирования стоимости денег во времени используются соответственно номинальная и реальная ставка процента.
Номинальная процентная ставка характеризует ставку процента, устанавливаемую без учета изменения покупательной способности денег в связи с инфляцией (или общую процентную ставку, в которой не элиминирована ее инфляционная составляющая).
Реальная процентная ставка характеризует ставку процента, устанавливаемую с учетом изменения покупательной стоимости в рассматриваемом периоде в связи с инфляцией.
С учетом рассмотренных базовых понятий формируется конкретный методический инструментарий, позволяющий учесть фактор инфляции в процессе управления финансовой деятельностью предприятия. Этот методический инструментарий дифференцируется в разрезе следующих основных вычислений (рис. 3.7).
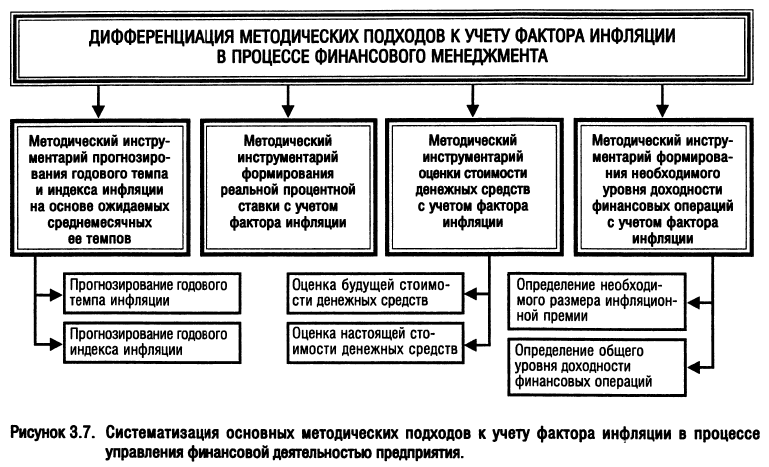
I. Методический инструментарий прогнозирования годового темпа и индекса инфляции основывается на ожидаемых среднемесячных ее темпах. Такая информация содержится в публикуемых прогнозах экономического и социального развития страны на предстоящий период. Результаты прогнозирования служат основой последующего учета фактора инфляции в финансовой деятельности предприятия.
1. При прогнозировании годового темпа инфляции используется следующая формула:
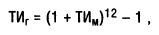
где ТИг — прогнозируемый годовой темп инфляции, выраженный десятичной дробью;
ТИм — ожидаемый среднемесячный темп инфляции в предстоящем периоде, выраженный десятичной дробью.
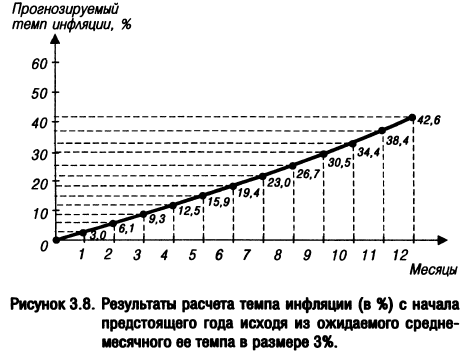
По указанной формуле может быть рассчитан не только прогнозируемый годовой темп инфляции, но и значение этого показателя на конец любого месяца предстоящего года. Это может быть проиллюстрировано графически исходя из условия рассмотренного примера (рис. 3.8).
2. При прогнозировании годового индекса инфляции используются следующие формулы:
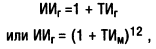
где ИИг — прогнозируемый годовой индекс инфляции, выраженный десятичной дробью;
ТИг — прогнозируемый годовой темп инфляции, выраженный десятичной дробью (рассчитанный по ранее приведенной формуле);
ТИм — ожидаемый среднемесячный темп инфляции, выраженный десятичной дробью.
II. Методический инструментарий формирования реальной процентной ставки с учетом фактора инфляции основывается на прогнозируемом номинальном ее уровне на финансовом рынке (результаты такого прогноза отражены обычно в ценах фьючерсных и опционных контрактов, заключаемых на фондовой бирже) и результатах прогноза годовых темпов инфляции. В основе расчета реальной процентной ставки с учетом фактора инфляции лежит Модель Фишера, которая имеет следующий вид:
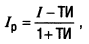
где Iр — реальная процентная ставка (фактическая или прогнозируемая в определенном периоде), выраженная десятичной дробью;
I — номинальная процентная ставка (фактическая или прогнозируемая в определенном периоде), выраженная десятичной дробью;
ТИ — темп инфляции (фактический или прогнозируемый в определенном периоде), выраженный десятичной дробью.
III. Методический инструментарий оценки стоимости денежных средств с учетом фактора инфляции позволяет осуществлять расчеты как будущей, так и настоящей их стоимости с соответствующей "инфляционной составляющей". В основе осуществления этих расчетов лежит формируемая реальная процентная ставка.
1. При оценке будущей стоимости денежных средств с учетом фактора инфляции используется следующая формула (представляющая собой модификацию рассмотренной ранее Модели Фишера):
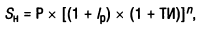
где Sн — номинальная будущая стоимость вклада (денежных средств), учитывающая фактор инфляции;
Р — первоначальная сумма вклада;
Iр — реальная процентная ставка, выраженная десятичной дробью;
ТИ — прогнозируемый темп инфляции, выраженный десятичной дробью;
n — количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.
2. При оценке настоящей стоимости денежных средств с учетом фактора инфляции используется следующая формула:
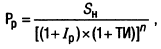
где Рp — реальная настоящая сумма вклада (денежных средств), учитывающая фактор инфляции;
Sн — ожидаемая номинальная будущая стоимость вклада (денежных средств);
Iр — реальная процентная ставка, используемая в процессе дисконтирования стоимости, выраженная десятичной дробью;
ТИ — прогнозируемый темп инфляции, выраженный десятичной дробью;
n — количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.
4. Методический инструментарий формирования необходимого уровня доходности финансовых операций с учетом фактора инфляции, с одной стороны, призван обеспечить расчет суммы и уровня "инфляционной премии", а с другой — расчет общего уровня номинального дохода, обеспечивающего возмещение инфляционных потерь и получение необходимого уровня реальной прибыли.
Инфляционная премия характеризует дополнительный доход, выплачиваемый (или предусмотернный к выплате) кредитору или инвестору с целью возмещения финансовых потерь от обесценения денег в связи с инфляцией. Уровень этого дохода обычно приравнивается к темпу инфляции.
1. При определении необходимого размера инфляционной премии используется следующая формула:
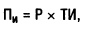
где Пи — сумма инфляционной премии в определенном периоде;
Р — первоначальная стоимость денежных средств;
ТИ — темп инфляции в рассматриваемом периоде, выраженный десятичной дробью.
2. При определении общей суммы необходимого дохода по финансовой операции с учетом фактора инфляции используется следующая формула:
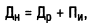
где Дн — общая номинальная сумма необходимого дохода по финансовой операции с учетом фактора инфляции в рассматриваемом периоде;
Др — реальная сумма необходимого дохода по финансовой операции в рассматриваемом периоде, исчисленная по простым или сложным процентам с использованием реальной процентной ставки;
Пи — сумма инфляционной премии в рассматриваемом периоде.
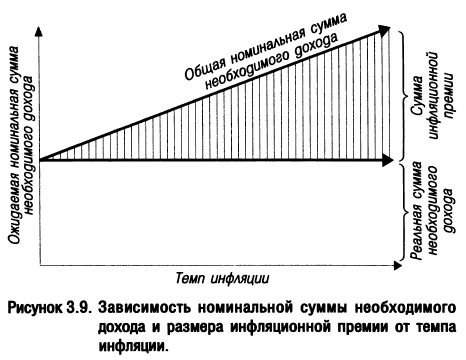
Зависимость общей суммы необходимого дохода и размера инфляционной премии от темпа инфляции может быть представлена графически (рис. 3.9).
3. При определении необходимого уровня доходности финансовых операций с учетом фактора инфляции используется следующая формула:
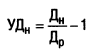
где УДн — необходимый уровень доходности финансовых операций с учетом фактора инфляции, выраженный десятичной дробью;
Дн — общая номинальная сумма необходимого дохода по финансовой операции в рассматриваемом периоде;
Др — реальная сумма необходимого дохода по финансовой операции в рассматриваемом периоде.
Следует отметить, что прогнозирование темпов инфляции представляет собой довольно сложный и трудоемкий вероятностный процесс, в значительной степени подверженный влиянию субъективных факторов. Поэтому в практике финансового менеджмента может быть использован более простой способ учета фактора инфляции. В этих целях стоимость денежных средств при их последующем наращении или размер необходимого дохода при последующем его дисконтировании пересчитывается заранее из национальной валюты в одну из "сильных" (т.е. в наименьшей степени подверженных инфляции) свободно конвертируемых валют по курсу на момент проведения расчетов. Процесс наращения или дисконтирования стоимости осуществляется затем по реальной процентной ставке (минимальной реальной норме прибыли на капитал). Такой способ оценки настоящей или будущей стоимости необходимого дохода позволяет вообще исключить из ее расчетов фактор инфляции внутри страны.