Концепция бета-коэффициента

Показатели средней акции, по определению, должны варьировать в соответствии с изменениями ситуации на рынках, измеряемыми биржевыми индексами. Средняя акция имеет β-коэффициент, равный 1,0. Это значит, что, например, при изменении ситуации на рынке вверх или вниз на один процентный пункт характеристики акции меняются в том же направлении на один процентный пункт.

Если акция имеет β = 0,5, ее характеристики будут меняться в два раза медленнее, чем в среднем на рынке. Портфель, состоящий из таких акций, будет иметь риск, равный половине риска портфеля из всех акций рынка, имеющего β = 1,0. Если β = 2,0, то изменчивость характеристик акции в два раза выше по сравнению со средней акцией, поэтому портфель, состоящий из таких акций, имеет риск в два раза больше среднего портфеля.

Бета-коэффициент портфеля ценных бумаг рассчитывается по формуле средней арифметической взвешенной:

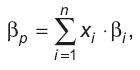
где х_i и β_i — доля и бета-коэффициент i-й ценной бумаги в портфеле; n — число ценных бумаг в портфеле.

Добавление в портфель акции, имеющей β больше единицы, увеличивает значение β и повышает рисковость портфеля, и наоборот.

Расчет бета-коэффициентов. Величины фактической доходности конкретной акции и доходности на рынке акций в среднем по календарным периодам оказываются взаимосвязаны. Эта взаимосвязь выражается линейной регрессионной зависимостью, которую можно получить путем статистической обработки данных биржевой статистики:

a_i = α_i +β_i⋅a_M +ε,

где a_i — доходность i-й акции; a_M — доходность рынка в среднем; α_i и β_i — коэффициенты уравнения регрессии; ε — случайная ошибка.