Анализ доходности и риска активов в портфеле

Ожидаемая доходность портфеля — набора активов представляет собой взвешенную среднюю из показателей ожидаемой доходности отдельных активов, входящих в данный портфель:

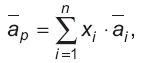
где a_p — ожидаемая доходность портфеля; x_i — доля стоимости портфеля, инвестированная в i-й актив; a — ожидаемая доходность i-го актива; i — порядковый номер актива; n — число активов в портфеле.

Риск портфеля в большинстве случаев меньше риска входящих в его состав активов. Для измерения риска портфеля необходимо вычислять среднеквадратическое отклонение его доходности. При дискретном распределении доходности его оценивают, определив дисперсию доходности портфеля следующим образом:

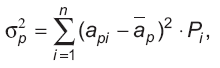
где σ²_p — дисперсия доходности портфеля; σ_p — среднеквадратическое отклонение доходности портфеля; a_p — ожидаемая доходность портфеля; a_pi — ожидаемая доходность портфеля при i-м состоянии экономики; P_i — вероятность i-го состояния экономики; n — число возможных состояний экономики.

Ковариация — мера, учитывающая дисперсию, — разброс индивидуальных значений доходности акции и силу связи между изменением доходности данной акции и других акций. Например, ковариация между акциями А и В показывает, существует ли взаимосвязь между увеличением или уменьшением значения доходности этих акций. Ковариация рассчитывается так:

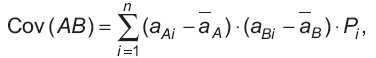
где Cov(AB) — ковариация доходности акций А относительно доходности акций B; — ожидаемая доходность акций А; a_А — ожидаемая доходность акций А при i-м состоянии экономики; — ожидаемая доходность акций B; a_B — ожидаемая доходность акций B при i-м состоянии экономики; P_i — вероятность i-го состояния экономики; n — число возможных состояний экономики.

Содержательно интерпретировать численное значение ковариации сложно, поэтому чаще используется другая статистическая характеристика, называемая коэффициентом корреляции. Корреляцией называется тенденция двух переменных к совместному изменению. Сила этой тенденции измеряется с помощью коэффициента, который лежит в пределах от +1,0, что означает тождественное изменение переменных, до -1,0, что означает изменение значений двух переменных абсолютно противоположным образом. Равенство коэффициента корреляции нулю указывает на отсутствие связи между переменными. Коэффициент корреляции между переменными А и В рассчитывается следующим образом:

где r_AB — коэффициент корреляции между доходностью акций А и В; σ_A — среднеквадратическое отклонение доходности акций A; σ_B — среднеквадратическое отклонение доходности акций B.