Измеритель риска - йота-коэффициент

Коэффициент вариации — йота-коэффициент.

В общем случае величина доходности и колеблемость, т.е. изменчивость доходности, могут быть различны. Для оценки меры относительного риска инвестиций с различной ожидаемой доходностью рассчитывают риск, приходящийся на единицу доходности. Делают это путем определения коэффициента вариации доходности. Этот коэффициент, который часто называют йота-коэффициентом, представляет собой отношение среднего квадратического отклонения к ожидаемому значению доходности:

I = σ / a,

где І — коэффициент вариации доходности — йота-коэффициент; σ — среднее квадратическое отклонение доходности; a — ожидаемая доходность.

субъективные и объективные распределения вероятностей. При построении распределений вероятностей могут использоваться субъективные экспертные оценки риска и доходности в будущем. Могут использоваться и фактические данные, что позволяет получить объективные, а не субъективные оценки. Например, это могут быть данные о доходности акций за последние годы, которые будут оценкой ожидаемых величин доходности и дисперсии. Они подсчитываются следующим образом:

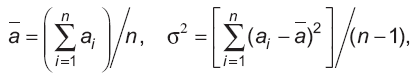
где a — ожидаемая доходность; σ² — дисперсия доходности; a_i — i-е измеренное значение доходности; n — число измерений доходности, например число членов временного ряда.

Анализ свойств субъективных и объективных распределений вероятностей приводит к выводу, что в финансовом анализе приходится сталкиваться с двумя источниками риска:

неопределенность исходов при заданном распределении вероятностей;
неточности используемых распределений вероятностей.

Распределения вероятностей и доверительные интервалы. Значительная часть данных, используемых в финансовом анализе, имеет нормальное распределение. Свойства нормального распределения точно определяют связь между величинами интервала, в котором с определенной доверительной вероятностью реализуются исходы событий по получению определенной доходности, и средним квадратичес-ким отклонением. Так, 68,3% всех исходов лежит в пределах одного отклонения в каждую сторону, которое равно среднему квадратическому отклонению от ожидаемого значения, 99,5% — в пределах отклонений, равных двум средним квадратическим отклонениям.