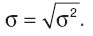Риск отдельных финансовых активов

Риск — это «возможная опасность», а также «действия на удачу в надежде на счастливый исход». Менеджеры, принимая инвестиционные и другие решения, должны оценивать риск и определять, компенсируется ли он ожидаемой доходностью. Риск можно определить двояко:

1. как общий риск (total risk), относящийся к конкретному активу, рассматриваемому изолированно, и измеряемый дисперсией ожидаемой доходности этого актива;
2. как рыночный риск (market risk), относящийся к конкретному активу как части портфеля активов и оцениваемый с учетом вклада этого актива в совокупный риск портфеля в целом.

При управлении активами необходимо сопоставление риска с ожидаемой доходностью, определение величины доходности, способной компенсировать данный уровень риска.

Поскольку риск связан с вероятностью того, что фактическая доходность окажется ниже ожидаемого значения, то основой для измерения риска являются статистические распределения вероятностей доходности. Распределением вероятностей называется множество возможных исходов событий с указанием вероятности появления каждого из них. ожидаемая доходность — наиболее вероятная величина доходности, величина, которую в теории вероятности принято называть математическим ожиданием.

Если число таких исходов конечно, то имеет место дискретное распределение вероятностей. В этом случае ожидаемую величину доходности (expected rate of return — ERR) можно представить в следующем виде:

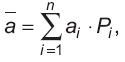
где a — ожидаемая доходность; a_i — i-й возможный исход, вариант событий; P_i — вероятность появления i-го исхода; n — число возможных исходов.

Дискретное распределение вероятностей может быть получено в результате экспертной оценки.

Дисперсией называется мера разброса возможных исходов относительно ожидаемого значения, причем чем выше дисперсия, тем больше разброс. Дисперсия дискретного распределения просчитывается следующим образом:

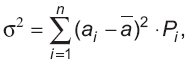
где σ² — дисперсия доходности.

Дисперсия — это сумма квадратов отклонений от ожидаемого значения, взвешенная на вероятность каждого отклонения.

Другим измерителем разброса индивидуальных значений вокруг среднего является среднее квадратическое, или стандартное отклонение, — квадратный корень из дисперсии: