Модели авторегрессии

Моделью авторегрессии называется динамическая эконометрическая модель, в которой в качестве факторных переменных содержатся лаговые значения результативной переменной.

Пример модели авторегрессии:

y_t=β₀+β₁x_t+δ₁y_t–1+ε_t,

где β₁ – это коэффициент, который характеризует краткосрочное изменение переменной у под влиянием изменения переменной х на единицу своего измерения;

δ₁– это коэффициент, который характеризует изменение переменной у в текущий момент времени t под влиянием своего изменения в предыдущий момент времени (t–1).

Промежуточным мультипликатором называется произведение коэффициентов модели авторегрессии (β₁*δ₁).

Промежуточный мультипликатор отражает общее абсолютное изменение результативной переменной у в момент времени (t+1).

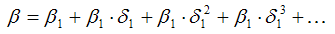
Определение. Долгосрочным мультипликатором называется показатель, рассчитываемый как

Долгосрочный мультипликатор отражает общее абсолютное изменение результативной переменной у в долгосрочном периоде.

Если для модели авторегрессии выполняется условие |δ|<1, то при наличии бесконечного лага будет справедливым равенство:

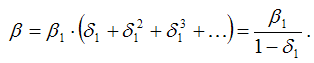
В нормальной линейной модели регрессии все факторные переменные не зависят от случайной ошибки модели. Данное условие для моделей авторегрессии нарушается, потому что переменная y_t–1 частично зависит от случайной ошибки модели ε_t. Следовательно, при оценке неизвестных коэффициентов традиционным методом наименьших квадратов ы получим смещённую оценку коэффициента при переменной y_t–1.

При определении оценок неизвестных коэффициентов модели авторегрессии используется метод инструментальных переменных (IV – Instrumental variables).

Суть метода инструментальных переменных заключается в том, что переменная y_t–1, для которой нарушается предпосылка применения метода наименьших квадратов, заменяется на новую переменную z, удовлетворяющую двум требованиям:

1. данная переменная должна тесно коррелировать с переменной y_t–1: cov(y_t–1,z)≠0;
2. данная переменная не должна коррелировать со случайной ошибкой модели ε_t: cov(z,ε)=0.

Предположим, что на основании собранных данных была построена модель авторегрессии вида:

y_t=β₀+β₁x_t+δ₁y_t–1+ε_t.

Рассчитаем оценки неизвестных коэффициентов данной модели с помощью метода инструментальных переменных.

В данной модели авторегрессии переменная y_t коррелирует с переменной x_t, следовательно, переменная y_t–1 зависит от переменной x_t–1. Охарактеризуем данную корреляционную зависимость с помощью парной модели регрессии вида:

y_t–1=k₀+k₁x_t–1+u_t,

где k₀ ,k₁ – неизвестные коэффициенты модели регрессии;

u_t – случайная ошибка модели регрессии.

Обозначим выражение k₀+k₁x_t–1 через переменную z_t–1. Тогда модель регрессии для переменной y_t–1 примет вид:

y_t–1= z_t–1+u_t.

Новая переменная z_t–1 удовлетворяет свойствам, предъявляемым к инструментальным переменным:

1. она тесно коррелирует с переменной y_t–1: cov(z_t–1,y_t–1)≠0;
2. она коррелирует со случайной ошибкой исходной модели авторегрессии ε_t: cov(ε_t, z_t–1).

Таким образом, исходная модель авторегрессии может быть представлена следующим образом:

y_t=β₀+β₁x_t+δ₁(k₀+k₁x_t–1+u_t)+ε_t= β₀+β₁x_t+δ₁ z_t–1+ν_t,

где ν_t= δ₁ u_t+ ε_t.

На следующем этапе оценки неизвестных коэффициентов преобразованной модели рассчитываются с помощью традиционного метода наименьших квадратов. Эти оценки будут являться оценками неизвестных коэффициентов исходной модели авторегрессии.