Динамические эконометрические модели

Динамической эконометрической моделью называется модель, которая в настоящий момент времени учитывает значения входящих в неё переменных, относящихся не только к текущему, но и к предыдущему моментам времени.

В качестве примера динамических эконометрических моделей можно привести модели вида:

y_t=f(x_t,x_t–l),

y_t=f(x_t,y_t–l).

Модель регрессии вида:

y_t=f(x1…xn)=f(x_i) не относится к динамическим эконометрическим моделям.

1) Динамические эконометрические модели делятся на два основных типа:

2) динамические модели, в которых значения переменных, относящихся к прошлым моментам времени (лаговые значения), включены в модель с текущими значениями этих переменных. К таким моделям относятся:

а) модель авторегрессии;
б) модель с распределённым лагом.

Моделью авторегрессии называется динамическая эконометрическая модель, в которой в качестве факторных переменных содержатся лаговые значения результативной переменной.

Пример модели авторегрессии:

y_t=β₀+β₁x_t+δ₁y_t–1+ε_t.

Моделью с распределённым лагом называется динамическая эконометрическая модель, в которую включены не только текущие, но и лаговые значения факторных переменных.

Пример модели с распределённым лагом:

y_t=β₀+β₁x_t+β₂x_t–1+…+βLx_t–l+ε_t.

где L – это величина временного лага (запаздывания) между рядами;

3) динамические модели, в которые входят переменные, отражающие предполагаемый или желаемый уровень результативной переменной или одной из факторных переменных в определённый момент времени (t+1). Величина желаемого уровня является неизвестной и рассчитывается на основании той информации, которая имеется в наличии на предшествующий момент времени (t). В зависимости от способа расчёта желаемых переменных различают следующие виды моделей:

а) модель адаптивных ожиданий (МАО);
б) модель частичной (неполной) корректировки (МЧК)

Моделью адаптивных ожиданий называется динамическая эконометрическая модель, которая учитывает предполагаемое или желаемое значение факторной переменной x^*_t+1.

Общий вид модели адаптивных ожиданий:

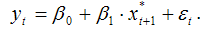
Примером модели адаптивных ожиданий является модель зависимости предполагаемой в будущем периоде (t+1) индексации заработных плат и пенсий на текущие цены.

Моделью частичной (неполной) корректировки называется динамическая эконометрическая модель, которая учитывает предполагаемое (или желаемое) значение результативной переменной y^*_t.

Общий вид модели частичной корректировки:

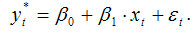
Примером модели частичной корректировки является модель Литнера, которая отражает зависимость желаемого объёма дивидендов y^*_t от фактического текущего объёма прибыли x_t.

Неизвестные коэффициенты динамических эконометрических моделей нельзя рассчитать с помощью традиционного метода наименьших квадратов, потому что они не будут удовлетворять свойствам несмещённости, состоятельности и эффективности.

Неизвестные коэффициенты моделей авторегрессии оцениваются с помощью метода инструментальных переменных.

Для моделей с распределённым лагом в зависимости от структуры лага для оценивания неизвестных коэффициентов применяются метод Алмон и метод Койка. Суть данных методов состоит преобразовании исходной модели с распределённым лагом к модели авторегрессии, оценки неизвестных параметров которой можно рассчитать с помощью метода инструментальных переменных.

Для определения оценок неизвестных коэффициентов модели адаптивных ожиданий и модели частичной корректировки их также преобразуют в модели авторегрессии.