Системы эконометрических уравнений

Если экономический процесс не поддаётся описанию посредством одной модели регрессии, то в подобных ситуациях прибегают к построению нескольких эконометрических уравнений, которые в совокупности образуют систему.

В состав системы эконометрических уравнений входят множество зависимых или эндогенных переменных и множество предопределённых переменных (лаговые и текущие независимые переменные, а также лаговые эндогенные переменные).

Системы эконометрических уравнений используются для объяснения текущих значений эндогенных переменных в зависимости от значений предопределённых переменных.

Системы эконометрических уравнений, которые используются в эконометрическом моделировании, подразделяются на три типа.

1. Система независимых эконометрических уравнений вида:

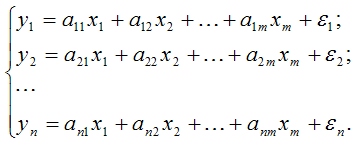
Данная система характеризуется тем, что каждая эндогенная переменная y является функцией от одних и тех же переменных x;

2. Система рекурсивных эконометрических уравнений вида:

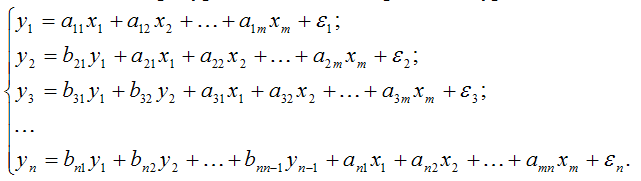
Данная система характеризуется тем, что в каждом последующем уравнении эндогенная переменная выступает в качестве экзогенной переменной;

3. Система взаимозависимых эконометрических уравнений вида:

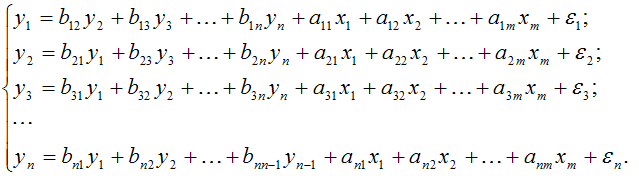
Данная система характеризуется тем, что эндогенные переменные в одних уравнениях входят в левую часть (т. е. являются результативными переменными), а в других уравнениях – в правую часть (т. е. являются факторными переменными).

В системе взаимозависимых уравнений значения результативных и факторных переменных формируются одновременно под влиянием внешних факторов. Поэтому данная система также называется системой одновременных или совместных уравнений.

В системах независимых и рекурсивных уравнений каждое уравнение может рассматриваться самостоятельно, поэтому оценки неизвестных коэффициентов этих уравнений можно рассчитать с помощью классического метода наименьших квадратов.

В системе одновременных уравнений каждое уравнение не может рассматриваться как самостоятельная часть системы, поэтому оценки неизвестных коэффициентов данных уравнений нельзя определить с помощью классического метода наименьших квадратов, т. к. нарушаются три основных условия применения этого метода:

а) между переменными системы уравнений существует одновременная зависимость, т. е. в первом уравнении системы y₁ является функцией от y₂, а во втором уравнении уже y₂ является функцией от y₁;

б) наличие проблема мультиколлинеарности, т. е. во втором уравнении системы y₂ зависит от x₁, а в других уравнениях обе переменные являются факторными;

в) случайные ошибки уравнения коррелируют с результативными переменными.

Следовательно, если неизвестные коэффициенты системы одновременных уравнений оценивать с помощью классического метода наименьших квадратов, то в результате мы получим смещённые и несостоятельные оценки.

Основной моделью системы одновременных уравнений является модель одновременного формирования спроса Q^d и предложения Q^s товара в зависимости от его цены P в момент времени t. Данная модель включает в себя три уравнения:

1) уравнение предложения:

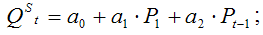
2) уравнение спроса:

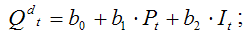
3) тождество спроса, справедливое при условии, что рынок находится в состоянии равновесия:

Q^s_t = Q^d_t

где

Q^s_t – предложение товара в момент времени t;

Q^d_t – спрос на товар в момент времени t;

P_t – цена товара в момент времени t;

P_t–1 – цена товара в предшествующий момент времени (t–1);

I_t – доход потребителей в момент времени t.