Методы фильтрации временного ряда

Методы фильтрации временных рядов предназначены на решение проблем, возникающих при исследовании взаимосвязи между двумя и более временными рядами, с помощью исключения из них трендовой и сезонной компонент.

К проблемам, которые позволяют устранить методы фильтрации временных рядов, относятся:

1) проблема ошибочности показателей тесноты и силы связи:

а) если временные ряды, между которыми изучается взаимосвязь, содержат циклическую или сезонную компоненту одинаковой периодичности, то в результате значение показателей тесноты связи будет завышено;

б) если один из временных рядов содержит циклическую или трендовую компоненту или периодичность совместных колебаний различна, то в результате значение показателей тесноты связи будет занижено;

2) проблема «ложной корреляции»:

а) если временные ряды, между которыми изучается взаимосвязь, содержат тренды одинаковой направленности, то уровни этих рядов будут положительно коррелированны;

б) если временные ряды, между которыми изучается взаимосвязь, содержат тренды противоположной направленности, то уровни этих рядов будут отрицательно коррелированны.

Первая проблема решается путём исключения из временного ряда сезонной компоненты.

Если временной ряд представлен в виде аддитивной модели, то сезонная компонента устраняется путём вычитания из исходных уровней ряда показателей абсолютных отклонений Sa_i.

Если временной ряд представлен в виде мультипликативной модели, то сезонная компонента устраняется путём деления исходных уровней ряда на индексы сезонности Is_i.

Проблема “ложной корреляции” решается путём исключения из временного ряда трендовой компоненты.

Предположим, что исследуется зависимость между двумя временными рядами – Х и Y. При этом была построена модель регрессии вида:

Y_t=β₀+β₁*Х_t+εt.

Для выявления «ложной корреляции» необходимо провести анализ остатков данной модели регрессии, потому что если в модели присутствует обычная автокорреляция остатков, следовательно, существует и «ложная автокорреляция».

Исключение трендовой компоненты осуществляется с помощью метода отклонений от тренда.

Алгоритм реализации метода отклонений от тренда:

1) вычисляются отклонения уровней временных рядов Y_t и X_t от их значений, рассчитанных на основе уравнений тренда:

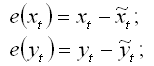
2) определяется степень тесноты связи между полученными отклонениями с помощью коэффициента корреляции:

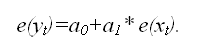
3) для линейной модели регрессии строится модель зависимости отклонения e(y_t) от e(x_t):

e(y_t)=a₀+a₁* e(x_t).

Неизвестные коэффициенты данной модели рассчитываются с помощью классического метода наименьших квадратов по формулам:

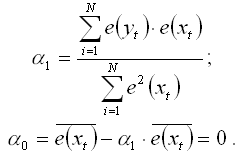
В результате получим модель вида:

e(y_t)=a₁* e(x_t).

Исключение трендовой компоненты можно также осуществить с помощью метода последовательных разностей. При этом рассчитываются разности между текущим и предыдущим уровнями для каждого временного ряда:

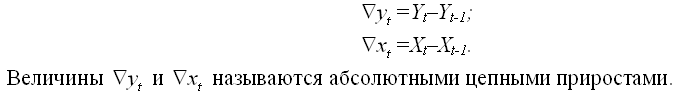
Далее рассчитывается показатель линейной корреляции абсолютных цепных приростов по формуле:

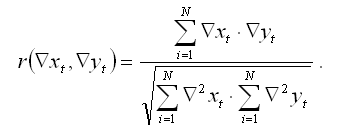
На основании показателей абсолютных цепных приростов можно построить линейную модель регрессии вида:

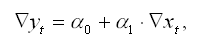
где а1 – это коэффициент, который уравнении характеризует в среднем прирост Y при изменении прироста Х на единицу своего измерения;

а0 – это коэффициент, который характеризует прирост Y при нулевом приросте Х.

С помощью разностных операторов первого порядка можно исключить автокорреляцию только в тех временных рядах, в которых основная тенденция выражена прямой линией.

С помощью разностных операторов второго порядка можно исключить автокорреляцию в тех временных рядах, в которых основная тенденция выражена параболой второго порядка.