Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:
εi=yi–β0–β1x1i–…–βmxmi
В связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается выборочная оценка случайной ошибки модели регрессии по формуле:
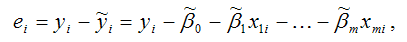
где ei – остатки модели регрессии.
Термин гетероскедастичность в широком смысле понимается как предположение о дисперсии случайных ошибок модели регрессии.
При построении нормальной линейной модели регрессии учитываются следующие условия, касающиеся случайной ошибки модели регрессии:
6) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
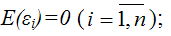
7) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:
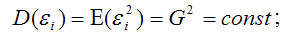
8) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
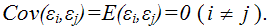
Второе условие
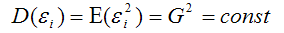
означает гомоскедастичность (homoscedasticity – однородный разброс) дисперсий случайных ошибок модели регрессии.
Под гомоскедастичностью понимается предположение о том, что дисперсия случайной ошибки βi является известной постоянной величиной для всех наблюдений.
Но на практике предположение о гомоскедастичности случайной ошибки βi или остатков модели регрессии ei выполняется не всегда.
Под гетероскедастичностью (heteroscedasticity – неоднородный разброс) понимается предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, что означает нарушение второго условия нормальной линейной модели множественной регрессии:
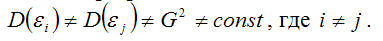
Гетероскедастичность можно записать через ковариационную матрицу случайных ошибок модели регрессии:
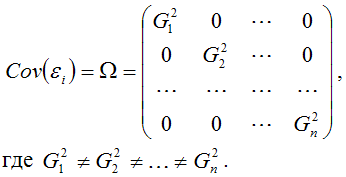
Тогда можно утверждать, что случайная ошибка модели регрессии βi подчиняется нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2Ω:
εi~N(0; G2Ω),
где Ω – матрица ковариаций случайной ошибки.
Если дисперсии случайных ошибок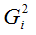 
модели регрессии известны заранее, то проблема гетероскедастичности легко устраняется. Однако в большинстве случаев неизвестными являются не только дисперсии случайных ошибок, но и сама функция регрессионной зависимости y=f(x), которую предстоит построить и оценить.
Для обнаружения гетероскедастичности остатков модели регрессии необходимо провести их анализ. При этом проверяются следующие гипотезы.
Основная гипотеза H0 предполагает постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности:
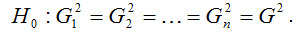
Альтернативная гипотеза H1 предполагает непостоянство дисперсиий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности:
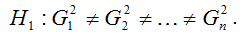
Гетероскедастичность остатков модели регрессии может привести к негативным последствиям:
1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности;
2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.