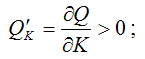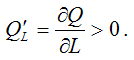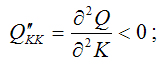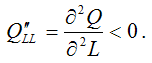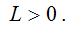Двухфакторная производственная функция Кобба-Дугласа
Теория производственных функций была разработана американскими учёными Д. Коббом и П. Дугласом, опубликовавшими в 1928 г. опубликовали работу «Теория производства».
Эти учёные предложили одну из наиболее известных разновидностей производственных функций, носящей название функции Кобба-Дугласа.
Общий вид функции Кобба-Дугласа:
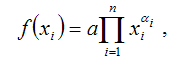
где а – числовой параметр производственной функции;
xi – i-тый аргумент или i-ый фактор производственной функции;
ai – показатель степени i-го аргумента.
Наиболее часто применяется двухфакторная форма функции Кобба-Дугласа f(K,L):
Q=A*Ka*Lβ,
где Q – объём выпущенной продукции (в стоимостном или натуральном выражении);
K – объём основного капитала или основных фондов;
L – объём трудовых ресурсов или трудовых затрат (измеряемое количеством рабочих или количеством человеко-дней).
A,a,β – неизвестные числовые параметры производственной функции, которые подчиняются условиям:
- 0≤а≤1;
- 0≤β≤1;
- A›0;
- a+β=1.
На основании четвёртного условия a+β=1, функция Кобба-Дугласа может быть представлена в виде:
Q=A*Ka*L1-а.
Данная производственная функция позволяет объяснить уровень совокупного выпуска Q количествами затраченного капитала K и труда L основных факторов производства.
На двухфакторную функцию Кобба-Дугласа накладываются определённые ограничения, которые необходимо учитывать при спецификации модели:
Первое и второе ограничения означают, что объём выпускаемой продукции увеличивается при постоянном значении одного из факторов и росте другого фактора. Однако если один из факторов производства фиксирован, а другой фактор возрастает, то каждая дополнительная (предельная) единица возрастающего фактора менее полезна (с точки зрения прироста выпуска продукции), чем предыдущая единица.
Третье и четвёртное ограничения означают, что при фиксированном значении одного из факторов последовательное увеличение другого фактора будет приводить к сокращению прироста значения Q.
Пятое и шестое ограничения означают, что каждый из факторов производства необходим в том смысле, что если один из факторов равен нулю (K=0 или L=0), то и объём производства также равен нулю Q=0.