Производственные функции

Производственной функцией называется экономико-математическая модель, с помощью которой можно охарактеризовать зависимость результатов производственной деятельности предприятия, отрасли или национальной экономики в целом от повлиявших на эти результаты факторов.

Факторами производственной функции могут являться следующие переменные:

1. объём выпущенной продукции (в стоимостном или натуральном выражении);
2. объём основного капитала или основных фондов;
3. объём трудовых ресурсов или трудовых затрат (измеряемое количеством рабочих или количеством человеко-дней);
4. затраты электроэнергии;
5. количество станков, потребляемое в производстве и др.

Однофакторные производственные функции (т. е. функции с одной факторной переменной) относятся к наиболее простым производственным функциям. В данном случае результативной переменной является объём производства у, который зависит от единственной факторной переменной х. В качестве факторной переменной может выступать любая из вышеназванных переменных.

Основными разновидностями однофакторных производственных функций являются:

1) линейная однофакторная производственная функция вида:

y=β₀+β₁x,

например, производственная функция зависимости объёма производимой продукции от величины затрат определённого ресурса. Линейная однофакторная производственная функция характеризуется двумя особенностями:

а) если величина факторной переменной х равна нулю, то объём производства у не будет нулевым, потому что y=β₀(β₀›0);

б) объём произведённой продукции у неограниченно возрастает при увеличении затрат определённого фактора х на постоянную величину β₁ (β₁›0). Однако данное свойство линейной однофакторной производственной функции чаще всего справедливо только на практике;

2) параболическая однофакторная производственная функция вида:

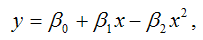
при условиях β₀›0, β₁›0, β₂›0.

Данная функция характеризуется тем, что при росте затрат ресурса х, объём произведённой продукции у вначале возрастает до некоторой максимальной величины, а затем снижается до нуля;

3) степенная однофакторная производственная функция вида:

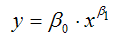
при условиях β₀›0, β₁›0.

Данная функция характеризуется тем, что с ростом затрат ресурса х, объём производства у возрастает без ограничений;

4) показательная однофакторная производственная функция вида:

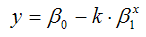
при условиях 0‹β₁‹0.

Данная функция характеризуется тем, что с ростом затрат ресурса х объём произведённой продукции у также растёт, стремясь при этом к значению параметра β₀.

5) гиперболическая однофакторная производственная функция вида:

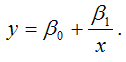
Данная функция практически не применяется при изучении зависимости объёма производства от затрат какого-либо ресурса, потому что нет необходимости в изучении ресурсов, увеличение которых приводит к уменьшению объёма производства.

Двухфакторные производственные функции (функции с двумя факторными переменными) характеризуют зависимость объёма производства от каких-либо двух факторов, чаще от факторов объёма основного капитала и трудовых ресурсов. Чаще всего используются такие двухфакторные производственные функции как функции Кобба-Дугласа и Солоу.

Для наглядного изображения двухфакторных производственных функций строят графики семейства кривых, основанных на различном сочетании двух факторов, но дающих в результате одно и то же значение объёма выпуска продукции. Кривые, построенные на основании равенства f(x₁,x₂)=const, называются изоквантами.

Изоквантой называется сочетание минимально необходимых ресурсных затрат для заданного уровня объёма производства.

Многофакторные производственные функции используются для изучения зависимости объёма производства от n-го количества факторов производства.

Общий вид многофакторной производственной функции:

y=f(x_i),

где i=1,n;