Метод наименьших квадратов для моделей регрессии, нелинейных по оцениваемым коэффициентам

Показательная функция вида 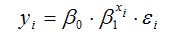является нелинейной по коэффициенту β₁ и относится к классу моделей регрессии, которые можно с помощью преобразований привести к линейному виду. Данная модель характеризуется тем, что случайная ошибка ε_i мультипликативно связана с факторной переменной хi. Следовательно, для определения оценок неизвестных коэффициентов данной модели можно применить классический метод наименьших квадратов.

Данную модель можно привести к линейному виду с помощью логарифмирования:

Log y_i=log β₀+ хi* logβ₁+ logε_i.

Для более наглядного представления данной модели регрессии воспользуемся методом замен:

log y_i=Y_i;

log β₀=A;

logβ₁=B;

logε_i=E.

В результате произведённых замен получим окончательный вид показательной функции, приведённой к линейной форме:

Y_i=A+Bхi+E.

Таким образом, мы будем применять метод наименьших квадратов не к исходной форме показательной функции, а к её преобразованной форме.

Для определения неизвестных коэффициентов линеаризованной формы показательной функции методом наименьших квадратов необходимо минимизировать сумму квадратов отклонений логарифмов наблюдаемых значений результативной переменной у от теоретических значений y˜ (значений, рассчитанных на основании модели регрессии), т. е. минимизировать функционал МНК вида:

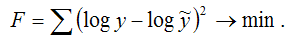
Оценки неизвестных коэффициентов А и В линеаризованной формы показательной функции находятся при решении системы нормальных уравнений вида:

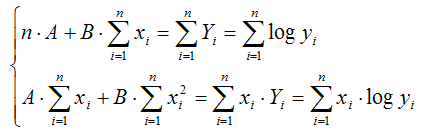
Данная система является системой нормальных уравнений относительно коэффициентов А и В для функции вида Y_i=A+Bхi+E.

Однако основным недостатком полученных МНК-оценок неизвестных коэффициентов моделей регрессии, сводимых к линейному виду, является их смещённость.