Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации

Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для моделей множественной регрессии, возможно также построение этих показателей с помощью показателя остаточной дисперсии.

В случае линейной модели парной регрессии показатель остаточной дисперсии определяется по формуле:

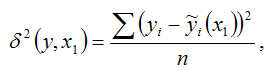
где

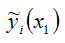– это оценка модели парной регрессии с независимой переменной х₁.

Если в линейную модель парной регрессии включить новую независимую переменную х₂, то можно вычислить показатель остаточной дисперсии для линейной модели регрессии с двумя независимыми переменными:

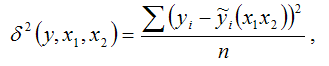
где

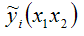– это оценка модели регрессии с двумя независимыми переменными х₁ и х₂.

Вне зависимости от качества построенной линейной модели двухфакторной регрессии будет справедливо неравенство вида:

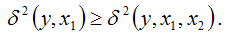
Тогда величину

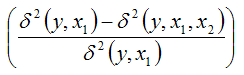
можно охарактеризовать как долю сокращения остаточной дисперсии за счёт включения в модель регрессии новой независимой переменной х₂. Чем больше величина данного показателя, тем сильнее дополнительная переменная х₂ влияет на результативную переменную у и на качество модели регрессии в целом.

Для линейной модели двухфакторной регрессии частный коэффициент корреляции между независимой переменной х₂ и результативной переменной у при постоянном значении независимой переменной х₁ через показатель остаточной дисперсии определяется по формуле:

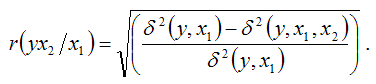
Для модели множественной регрессии с n независимыми переменными частный коэффициент корреляции (n-1) порядка независимой переменной х₁ и результативной переменной у при постоянном значении остальных независимых переменных, включённых в модель, определяется по формуле:

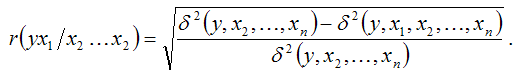
Показатель остаточной дисперсии результативной переменной и коэффициент множественной детерминации связаны отношением:

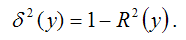
Если в формуле частного коэффициента корреляции выразить остаточную дисперсию результативной переменной с помощью коэффициента множественной детерминации, то для модели множественной регрессии с n независимыми переменными частный коэффициент корреляции в общем виде можно определить по формуле:

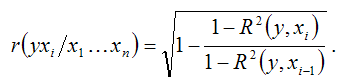
Частные коэффициенты корреляции, вычисленные через показатель остаточной дисперсии или коэффициент множественной детерминации, изменяются в пределах от нуля до единицы.

Частный коэффициент корреляции для модели множественной регрессии в общем случае характеризует степень зависимости между результативной переменной и одной из факторных переменных при постоянном значении остальных независимых переменных, включённых в модель регрессии.