Классический метод наименьших квадратов для модели множественной регрессии. Метод Крамера

В общем виде линейную модель множественной регрессии можно записать следующим образом:

y_i=β₀+β₁x_1i+…+β_mx_mi+ε_i,i=1,n;

где y_i – значение i-ой результативной переменной,

x_1i…x_mi – значения факторных переменных;

β₀…β_m – неизвестные коэффициенты модели множественной регрессии;

ε_i – случайные ошибки модели множественной регрессии.

В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Суть метода наименьших квадратов состоит в том, чтобы найти такой вектор β оценок неизвестных коэффициентов модели, при которых сумма квадратов отклонений (остатков) наблюдаемых значений зависимой переменной у от расчётных значений y˜ (рассчитанных на основании построенной модели регрессии) была бы минимальной.

Матричная форма функционала F метода наименьших квадратов:

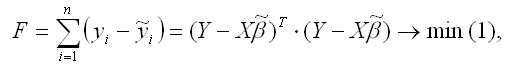
где

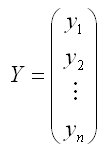– случайный вектор-столбец значений результативной переменной размерности (n*1);

– матрица значений факторной переменной размерности (n*(m+1)). Первый столбец является единичным, потому что в модели регрессии коэффициент β₀ умножается на единицу;

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β₀…β_m, потому что значения результативной и факторных переменных известны из наблюдений. Для определения минимума функции (1) необходимо вычислить частные производные этой функции по каждому из оцениваемых параметров и приравнять их к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (1):

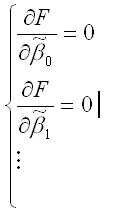
где

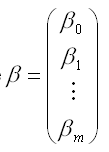– вектор-столбец неизвестных коэффициентов модели регрессии размерности ((m+1)*1);

Общий вид стационарной системы уравнений для функции (1):

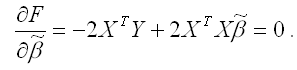
Решением стационарной системы уравнений будут МНК-оценки неизвестных параметров линейной модели множественной регрессии:

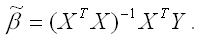
Оценим с помощью метода наименьших квадратов неизвестные параметры линейной модели двухфакторной регрессии:

y_i=β₀+β₁x_1i+β₂x2i+ε_i,

где

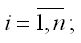
Чтобы рассчитать оценки неизвестных коэффициентов β₀,β₁ и β₂данной двухфакторной модели регрессии, необходимо минимизировать функционал F вида:

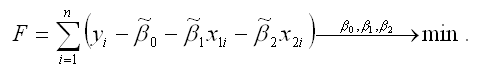
Для определения экстремума функции нескольких переменных, частные производные по этим переменным приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для модели множественной линейной регрессии с двумя переменными:

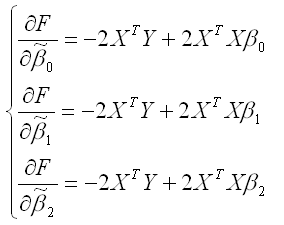
В результате элементарных преобразований данной стационарной системы уравнений получим систему нормальных уравнений:

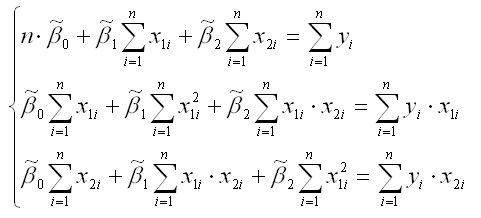
Данная система называется системой нормальных уравнений относительно коэффициентов 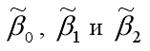для модели регрессии y_i=β₀+β₁x_1i+β₂x_2i+ε_i.

Полученная система нормальных уравнений является квадратной, т. к. количество уравнений равняется количеству неизвестных переменных, поэтому коэффициенты 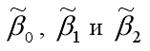можно рассчитать с помощью метода Крамера или метода Гаусса.

Рассмотрим подробнее метод Крамера решения квадратных систем нормальных уравнений.

Единственное решение квадратной системы линейных уравнений определяется по формуле:

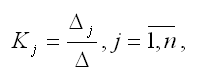
где Δ – основной определитель квадратной системы линейных уравнений;

Δj – определитель, полученный из основного определителя путём замены j-го столбца на столбец свободных членов.

При использовании метода Крамера возможно возникновение следующих ситуаций:

1) если основной определитель системы Δ равен нулю и все определители Δj также равны нулю, то данная система имеет бесконечное множество решений;

2) если основной определитель системы Δ равен нулю и хотя бы один из определителей Δj также равен нулю, то система решений не имеет.