Линейная модель множественной регрессии

Построение модели множественной регрессии является одним из методов характеристики аналитической формы связи между зависимой (результативной) переменной и несколькими независимыми (факторными) переменными.

Модель множественной регрессии строится в том случае, если коэффициент множественной корреляции показал наличие связи между исследуемыми переменными.

Общий вид линейной модели множественной регрессии:

y_i=β₀+β₁x_1i+…+β_mx_mi+ε_i,

где y_i – значение i-ой результативной переменной, i=1,n;

x_1i…x_mi – значения факторных переменных;

β₀…β_m – неизвестные коэффициенты модели множественной регрессии;

ε_i – случайные ошибки модели множественной регрессии.

При построении нормальной линейной модели множественной регрессии учитываются пять условий:

1) факторные переменные x_1i…x_mi – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии β_i;

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

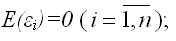
3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:

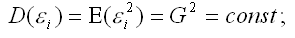
4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т.е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):

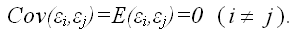
Это условие выполняется в том случае, если исходные данные не являются временными рядами;

5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G²: ε_i~N(0, G²).

Общий вид нормальной линейной модели парной регрессии в матричной форме:

Y=X* β+ε,

Где

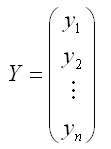– случайный вектор-столбец значений результативной переменной размерности (n*1);

– матрица значений факторной переменной размерности (n*(m+1)). Первый столбец является единичным, потому что в модели регрессии коэффициент β₀ умножается на единицу;

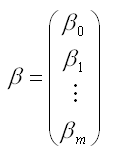– вектор-столбец неизвестных коэффициентов модели регрессии размерности ((m+1)*1);

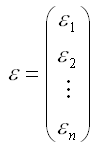– случайный вектор-столбец ошибок модели регрессии размерности (n*1).

Включение в линейную модель множественной регрессии случайного вектора-столбца ошибок модели обусловлено тем, что практически невозможно оценить связь между переменными со 100-процентной точностью.

Условия построения нормальной линейной модели множественной регрессии, записанные в матричной форме:

1) факторные переменные x_1j…x_mj – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии ε_i. В терминах матричной записи Х называется детерминированной матрицей ранга (k+1), т.е. столбцы матрицы X линейно независимы между собой и ранг матрицы Х равен m+1

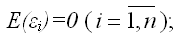
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

3) предположения о том, что дисперсия случайной ошибки модели регрессии является постоянной для всех наблюдений и ковариация случайных ошибок любых двух разных наблюдений равна нулю, записываются с помощью ковариационной матрицы случайных ошибок нормальной линейной модели множественной регрессии:

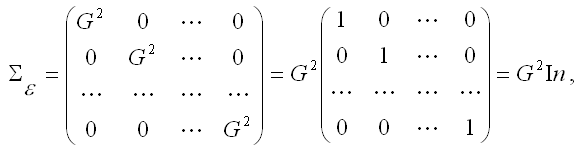
где

G² – дисперсия случайной ошибки модели регрессии ε;

In – единичная матрица размерности (n*n).

4) случайная ошибка модели регрессии ε является независимой и независящей от матрицы Х случайной величиной, подчиняющейся многомерному нормальному закону распределения с нулевым математическим ожиданием и дисперсией G²: ε→N(0;G²In.

В нормальную линейную модель множественной регрессии должны входить факторные переменные, удовлетворяющие следующим условиям:

1. данные переменные должны быть количественно измеримыми;
2. каждая факторная переменная должна достаточно тесно коррелировать с результативной переменной;
3. факторные переменные не должны сильно коррелировать друг с другом или находиться в строгой функциональной зависимости.