Точечный и интервальный прогнозы для модели парной регрессии

Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных моделей, с помощью которых можно спрогнозировать поведение результативной переменной в зависимости от поведения факторных переменных.

Рассмотрим подробнее процесс прогнозирования для линейной модели парной регрессии.

Точечный прогноз результативной переменнойу на основе линейной модели парной регрессии при заданном значении факторной переменной хm будет осуществляться по формуле:

ym=β₀+β₁xm+εm.

Точечный прогноз результативной переменной ym с доверительной вероятностью γ или (1–а) попадает в интервал прогноза, определяемый как:

ym–t*ω(m)≤ ym≤ ym+t*ω(m),

t – t-критерий Стьюдента, который определяется в зависимости от заданного уровня значимости a и числа степеней свободы (n-2) для линейной модели парной регрессии;

ω(m) – величина ошибки прогноза в точке m.

Для линейной модели парной регрессии величина ошибки прогноза определяется по формуле:

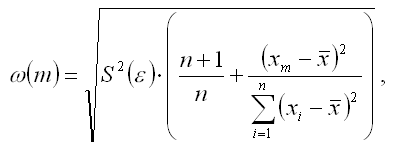
где S2(ε) – несмещённая оценка дисперсии случайной ошибки линейной модели парной регрессии.

Рассмотрим процесс определения величины ошибки прогноза β(m).

Предположим, что на основе выборочных данных была построена линейная модель парной регрессии вида:

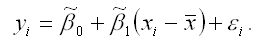
Факторная переменная х в данной модели представлена в центрированном виде.

Задача состоит в расчёте прогноза результативной переменной у при заданном значении факторной переменной хm, т. е.

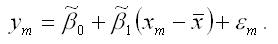
Математическое ожидание результативной переменной у в точке m рассчитывается по формуле:

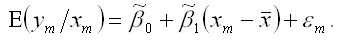
Дисперсия результативной переменной у в точке m рассчитывается по формуле:

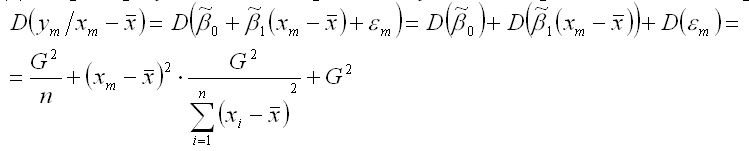
где D(β₀) – дисперсия оценки параметра β₀ линейной модели парной регрессии, которая рассчитывается по формуле:

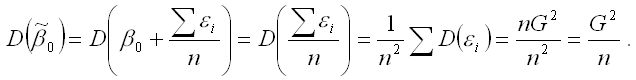
Следовательно, точечная оценка прогноза результативной переменной у в точке m имеет нормальный закон распределения с математическим ожиданием

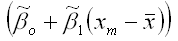
и дисперсией

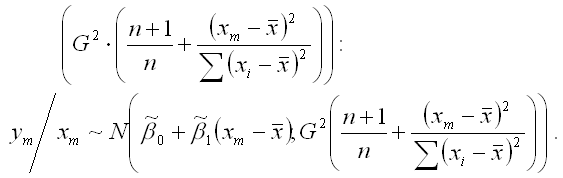
Если в формулу дисперсии результативной переменной у в точке m вместо дисперсии G2 подставить её выборочную оценку S2, то получим доверительный интервал для прогноза результативной переменной у при заданном значении факторной переменной хm:

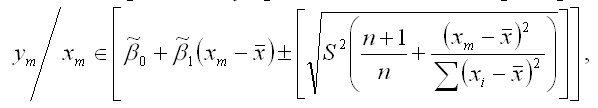
где выборочная оценка генеральной дисперсии S2 для линейной модели парной регрессии рассчитывается по формуле:

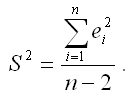
В этом случае прогнозный интервал можно преобразовать к виду:

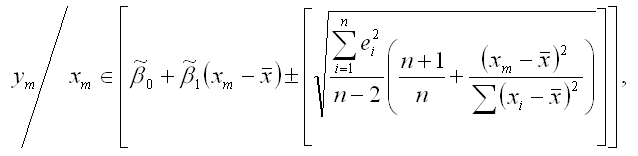
что и требовалось доказать.