Оценка дисперсии случайной ошибки модели регрессии

При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.

Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:

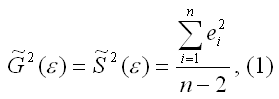
где n – это объём выборочной совокупности;

еi– остатки регрессионной модели:

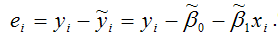
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:

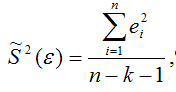
где k – число оцениваемых параметров модели регрессии.

Оценка матрицы ковариаций случайных ошибок Cov(ε) будет являться оценочная матрица ковариаций:

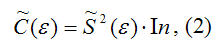
где In – единичная матрица.

Оценка дисперсии случайной ошибки модели регрессии распределена по ε2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.

Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства

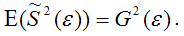
Доказательство. Примем без доказательства справедливость следующих равенств:

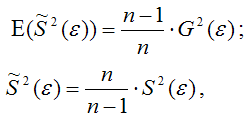
где G2(ε) – генеральная дисперсия случайной ошибки;

S2(ε) – выборочная дисперсия случайной ошибки;

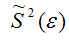– выборочная оценка дисперсии случайной ошибки.

Тогда:

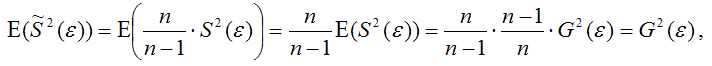
т. е.

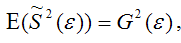
что и требовалось доказать.

Следовательно, выборочная оценка дисперсии случайной ошибки 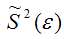является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(ε).

При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты β. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.

Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки 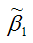от величины случайной ошибки ε.

МНК-оценка коэффициента β₁ модели регрессии определяется по формуле:

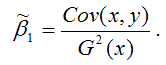
В связи с тем, что переменная у зависит от случайной компоненты ε (y_i=β₀+β₁x_i+ε_i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:

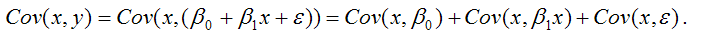
Для дальнейших преобразования используются свойства ковариации:

1. ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2. ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).

Исходя из указанных свойств ковариации, справедливы следующие равенства:

Cov(x,β₀)=0 (β₀=const);

Cov(x, β₁x)= β₁*Cov(x,x)= β₁*G2(x).

Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:

Cov(x,y)= β₁G2(x)+Cov(x,ε).

В результате МНК-оценка коэффициента β₁ модели регрессии примет вид:

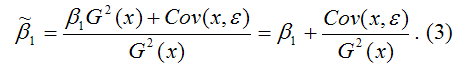
Таким образом, МНК-оценка 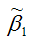может быть представлена как сумма двух компонент:

1. константы β₁, т. е. истинного значения коэффициента;
2. случайной ошибки Cov(x,ε), вызывающей вариацию коэффициента модели регрессии.

Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.

Аналогично доказывается, что МНК-оценка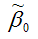 коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки 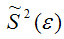могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ε.