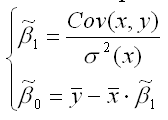Оценивание неизвестных коэффициентов модели регрессии методом наименьших квадратов. Теорема Гаусса – Маркова

Определение коэффициентов модели регрессии осуществляется на третьем этапе схемы построения эконометрической модели. В результате этой процедуры рассчитываются оценки (приближенные значения) неизвестных коэффициентов спецификации модели.

Спецификация линейной эконометрической модели из изолированного уравнения с гомоскедастичными возмущениями имеет вид:

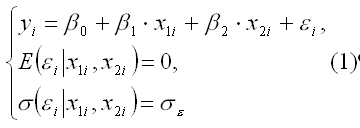
Рассмотрим метод наименьших квадратов на примере оценивания эконометрических моделей в виде моделей парной регрессии (изолированных уравнений с двумя переменными).

Если уравнение модели содержит две экономические переменные – эндогенную y_i и предопределенную x_i, то модель имеет вид:

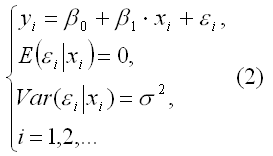
Данная модель называется моделью линейной парной регрессии и содержит три неизвестных параметра:

β₀, β₁, σ. (3)

Предположим, что имеется выборка: (х₁, y₁), (х₂, y₂),… (х_n, y_n) (4)

Тогда в рамках исследуемой модели данные величины связаны следующим образом:

y₁ = a₀ + a₁ * x₁ + u₁,

y₂ = a₀ + a₁ * x₂ + u₂, (5)

…

y_n= a₀ + a₁ * x_n + u_n.

Данная система называется системой уравнений наблюдения объекта в рамках исследуемой линейной модели или схемой Гаусса-Маркова.

Компактная запись схемы Гаусса-Маркова:

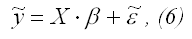
где

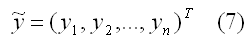– вектор-столбец известных значений эндогенной переменной yiмодели регрессии;

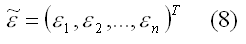– вектор-столбец неизвестных значений случайных возмущений ε_i;

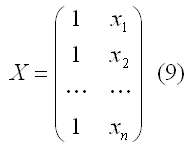– матрица известных значений предопределенной переменной xi модели;

β = (β₀ β₁ )Т (10) – вектор неизвестных коэффициентов модели регрессии.

Обозначим оценку вектора неизвестных коэффициентов модели регрессии как

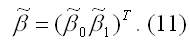
Данная оценка вычисляется на основании выборочных данных (7) и (9) с помощью некоторой процедуры:

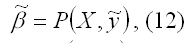
где P (X, y˜) – символ процедуры.

Процедура (12) называется линейной относительно вектора (7) значений эндогенной переменной yi, если выполняется условие:

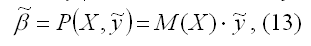
где

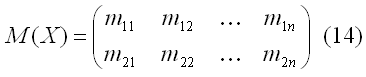
(14) – матрица коэффициентов, зависящих только от выборочных значений (9) предопределенной переменной хi.

Теорема Гаусса-Маркова. Пусть матрица Х коэффициентов уравнений наблюдений (6) имеет полный ранг, а случайные возмущения (8) удовлетворяют четырем условиям:

E(ε₁) = E(ε₂) = … = E(ε_n) = 0, (15)

Var(ε₁) = Var(ε₂) = … = Var(ε_n) = σ²(16)

Cov(ε_i, ε_j) = 0 при i≠j(17)

Cov(xi,ε_j) = 0 при всех значениях i и j (18)

В этом случае справедливы следующие утверждения:

а) наилучшая линейная процедура (13), приводящая к несмещенной и эффективной оценке (11), имеет вид:

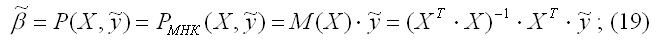
б) линейная несмещенная эффективная оценка (19) обладает свойством наименьших квадратов:

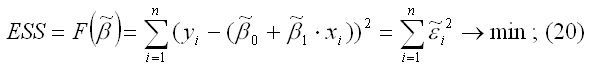
в) ковариационная матрица оценки (19) вычисляется по правилу:

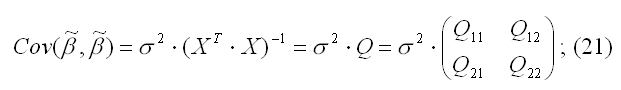
г) несмещенная оценка параметра σ² модели (2) находится по формуле:

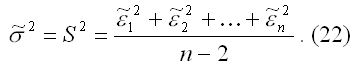
Следствие теоремы Гаусса-Маркова. Оценка 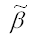доставляемая процедурой (19) метода наименьших квадратов, может быть вычислена в процессе решения системы двух линейных алгебраических уравнений:

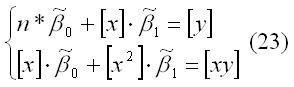
Данная система называется системой нормальных уравнений. Ее коэффициенты и свободные члены определяются по правилам:

[x] = x₁ + x₂ +…+ x_n,

[y] = y₁ + y₂ +…+ y_n, (24)

[x²] = x₁² + x₂² +…+ x_n²,

[xy] = x₁*y₁ + x₂*y₂ + … + x_n*y_n.

Явный вид решения системы (23):