Модель частичной (неполной) корректировки

Моделью частичной (неполной) корректировки называется динамическая эконометрическая модель, которая учитывает предполагаемое или желаемое значение результативной переменной y^*_t Общий вид модели частичной корректировки:

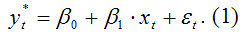
Предполагаемое значение переменной y^*_t в момент времени t рассчитывается на основании значений фактических (реальных) переменных в предшествующий момент времени (t-1).

Примером модели частичной корректировки является модель Литнера, которая характеризует зависимость желаемого объёма дивидендов y^*_t от фактического текущего объёма прибыли x_t.

В основе модели частичной корректировки лежит предположение о том, что величина фактического приращения результативной переменной в текущем периоде по сравнению с предшествующим периодом (y_t–y_t–1) пропорциональна разности между её ожидаемым уровнем и фактическим значением в предшествующий момент времени

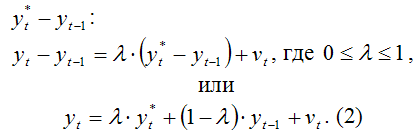
Следовательно, фактическое значение результативной переменной в момент времени t (y_t) определяется как среднее арифметическое взвешенное значение предполагаемого уровня результативной переменной в тот же самый момент времени (y^*_t) и фактического значений этой переменной в предшествующий момент времени _t–1 (y_t–1).

Величина λ называется параметром корректировки.

Чем больше значение параметра корректировки, тем быстрее осуществляется процесс корректировки результативной переменной y_t.

Если параметр корректировки равен единице, то фактическое значение результативной переменной равно её ожидаемому значению

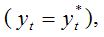
и процесс полной корректировки происходит за один период.

Если параметр корректировки равен нулю, то корректировка результативной переменной y_t не происходит вовсе.

Модель частичной корректировки содержит предполагаемые значения результативной переменной, которые нельзя получить эмпирическим путём, поэтому оценивание неизвестных коэффициентов модели с помощью традиционного метода наименьших квадратов невозможно.

Для определения оценок неизвестных коэффициентов исходной модели частичной корректировки (1) её необходимо преобразовать.

Подставим исходную модель (1) в выражение (2):

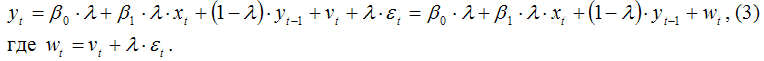
Оценки неизвестных параметров β₀, β₁ и λ преобразованной модели можно рассчитать с помощью традиционного метода наименьших квадратов.

Преобразованная модель (3) включает стохастическую объясняющую переменную y_t–1. Но данная переменная не коррелирует с текущим значением совокупной случайной ошибки модели w_t, потому что ошибки ε_t и ν_t определяются только после расчёта значения результативной переменной y_t–1. Поэтому оценки неизвестных коэффициентов, полученные с помощью традиционного метода наименьших квадратов, будут асимптотически несмещёнными и эффективными оценками.

Долгосрочной функцией модели частичной корректировки называется исходная модель (1), которая содержит предполагаемые значения результативной переменной.

Краткосрочной функцией модели частичной корректировки называется преобразованная модель (3), которая содержит только фактические значения переменных.