Методы экономического анализа
Классификация методов экономического анализа
Под методом экономического анализа обычно понимают диалектический способ подхода к изучению хозяйственных процессов в их становлении и развитии. Особенностью метода экономического анализа является то, что он использует систему показателей, которые на различных уровнях управления наиболее широко характеризуют субъект рыночных отношений, выявляет и измеряет тесноту взаимосвязи этих показателей. Необходимость такого подхода связана с тем, что изучение каждого показателя в отрыве от других порождает ошибочные выводы, затрудняя понимание глубинных процессов, происходящих в организации, выбор мероприятий, необходимых для совершенствования хозяйственной деятельности.
Исходя из этого метод экономического анализа представляет собой совокупность приемов и способов изучения хозяйственной деятельности предприятий путем выявления и определения взаимосвязей изучаемых показателей, расчленения их на составляющие и сравнения с другими, измерения величины влияния на изучаемые показатели как отдельных составляющих, так и совокупности их в единстве и взаимной связи.
На начальной стадии анализа того или иного показателя изучение проводится от общего к частному, что представляет собой дедуктивный прием исследования. На стадии обобщения изученные составляющие анализируемого показателя рассматриваются с учетом влияния их на общие анализируемые показатели, что представляет собой индуктивный прием исследования. Дедуктивный и индуктивный приемы исследования — это две стороны процесса изучения явлений. В этом проявляются единство и неразрывная связь анализа и синтеза. Применение каждого элемента метода достигается совокупностью технических приемов и способов экономического анализа.
В процессе экономического анализа, аналитической обработки экономической информации применяется ряд специальных способов и приемов.
Существует различная классификация методов и приемов экономического анализа, зависящая от исследуемых признаков.
Способы и приемы экономического анализа можно условно подразделить на две группы: формализованные и неформализованные.
Формализованные методы позволяют представить показатели в строгой зависимости (преимущественно математической). Среди них можно выделить:
- классические методы экономического анализа;
- методы факторного анализа;
- экономико-математические методы;
- графический метод и др.
К классическим способам и приемам экономического анализа относятся: метод абсолютных, относительных величин и средних величин, способ сравнения показателей; группировка; составление аналитических таблиц и др.
Среди методов факторного анализа можно выделить индексный метод; приемы элиминирования (способ абсолютных и относительных разниц, способ цепной подстановки), балансовый метод.
К экономико-математическим методам, достаточно широко используемым в экономическом анализе, можно отнести метод корреляционного и регрессионного анализа, кластерный анализ, эконометрические методы, методы математического программирования, теорию игр, теорию массового обслуживания, метод оптимизации товарных запасов (модель Уилсона) и др.
Графическим отражением результатов является изображение их на графиках при помощи тех или иных геометрических фигур, линий, точек — наиболее наглядный способ показа и характеристики анализируемых данных. В экономическом анализе применяют два основных вида графиков — диаграммы и картограммы.
В диаграммах отчетные данные изображаются в виде различных фигур и линий, а в картограммах — в виде условных обозначений на схемах. В зависимости от способа построения различают столбиковые, секторные (круговые), линейные и фигурные диаграммы.
Неформализованные методы основаны на отражении аналитических процедур на логическом уровне, а не на строгих аналитических зависимостях. К ним относят разработку системы показателей, метод экспертных оценок, методы ситуационного анализа, SWOT-анализа, PEST-анализа, метод функционально-стоимостного анализа, метод маржинального анализа и др.
Классические методы экономического анализа
Анализ тех или иных экономических показателей, явлений, процессов, ситуаций начинается с использования метода абсолютных величин, поскольку именно этот метод позволяет получить исходную информацию для анализа. С его помощью можно охарактеризовать масштабы хозяйственной деятельности организации, величину примененных и потребленных в процессе хозяйственной деятельности ресурсов, полученные результаты. При использовании данного метода применяют абсолютные показатели, рассмотренные выше (параграф 11.3).
Применение этого метода позволяет предварительно сориентироваться в итогах работы организации путем рассмотрения по данным, полученным из различных источников информации. Например, по данным отчетности можно охарактеризовать основные показатели хозяйственной деятельности: выполнение планов производства и продаж, доходов, расходов, наличие собственных средств, размер дебиторской задолженности и др. Этот метод позволяет получить общее представление об итогах хозяйственной деятельности и определить направления дальнейшего анализа, прежде всего, факторного, в процессе которого выявляется влияние факторов па имеющиеся показатели.
Метод абсолютных величин позволяет получить исходную информацию для применения других приемов и способов аналитического исследования объектов анализа.
Например, абсолютные величины используются в качестве базы для исчисления относительных и средних величин.
Как уже отмечалось выше, относительные показатели характеризуют соотношения каких-либо двух абсолютных показателей. Они определяются в процентах, коэффициентах или индексах.
Исчисление относительных величин, которые широко применяются в экономическом анализе, позволяет объективно оцепить хозяйственные процессы. Как правило, при анализе используют абсолютные (стоимостные, натуральные, трудовые) величины, но часто при их сравнении трудно сделать вывод (обобщение) о качестве выполнения плана или выявить тенденции изменения того или иного показателя. В этом случае используют относительные величины.
Относительные величины сравнения имеют большое значение в отраслевом анализе, а также при анализе и оценке конкурентных преимуществ, когда сравниваются одни и те же характеристики двух разных совокупностей, групп, единиц (доли рынка, занимаемые различными организациями).
Основное условие расчета относительной величины — сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Величина, с которой производится сравнение (знаменатель дроби), обычно называется базой сравнения или основанием.
Не менее существенны в экономическом анализе средние величины. Они предназначены для обобщения соответствующей совокупности типичных, однородных показателей, явлений, процессов. В средней величине сглаживаются количественные колебания отдельных показателей хозяйственной деятельности исследуемых объектов. На основе обобщения, усреднения частных показателей рассчитывается новый самостоятельный показатель, который может позволить выявить качественную сторону исследуемого процесса или явления. В среднем показателе случайные отклонения частных показателей взаимно погашаются, что позволяет абстрагироваться от случайности отдельных значений и колебаний. Без средних величин невозможно сравнение изучаемого признака по разным совокупностям и характеристикам изменения варьирующего показателя во времени. В аналитических расчетах применяются различные виды средних величин. Наиболее распространенными являются средняя арифметическая — простая и взвешенная. Используются также и другие формы средних величин: средняя хронологическая, средняя гармоническая взвешенная, средняя геометрическая и т.д. С помощью средних величин (групповых и общих), исчисленных на основе массовых данных о качественно однородных явлениях и процессах, можно выявить общие тенденции и даже закономерности в развитии объектов аналитического исследования. В то же время серьезным недостатком этого приема анализа является то, что за средними величинами могут скрываться значительные колебания значений частных изучаемых показателей, что может привести к неверным выводам, а значит и ошибочным управленческим решениям.
Сравнение — наиболее распространенный прием анализа. Иначе говоря, сравнение — научный метод познания, в процессе которого изучаемые явления и объекты сопоставляются с уже известными или изученными ранее с целью определения общих черт, либо различий между ними. Каждый показатель, используемый для оценки и контроля, имеет значение только в сопоставлении с другим.
Сравнение начинается с соотношения явлений, анализируются сравниваемые явления. Сравнение экономических показателей может осуществляться но разным направлениям:
- с плановыми (нормативными) показателями;
- со средними показателями по региону, отрасли;
- с аналогичными показателями прошлых периодов;
- с другими показателями деятельности организации и др.
Сопоставляя отчетные данные с плановыми (нормативными), выявляют степень выполнения (или невыполнения) планового задания. Сопоставление фактических показателей с нормативными (например, с нормами расходов сырья, материалов, энергии и др.) проводится в целях контроля за использованием всех видов ресурсов. Сравнение фактических показателей с утвержденными нормами необходимо также для выявления экономии или перерасходов отдельных видов ресурсов на производство продукции, для оценки утерянных возможностей выпуска продукции и снижения себестоимости.
Сопоставляя фактические данные исследуемой организации со средними показателями по региону, выявляют отличия показателей работы организации от средних по региону (но уровню оплаты труда работников, по величине совокупных ресурсов и т.д.).
Сопоставляя фактические показатели отчетного периода с аналогичными показателями ряда прошлых периодов, оценивают результаты работы в динамике. Сравнение фактически достигнутых результатов с данными прошлых периодов дает возможность оценить темпы изменения исследуемых показателей и определить тенденции развития экономических процессов в организации.
Сравнение показателей анализируемой организации со средними аналогичными показателями по отрасли выявляет место анализируемого субъекта па рынке среди других хозяйствующих субъектов, долю на рынке.
Сравнение показателей, характеризующих деятельность организации, со средними показателями других организаций данной отрасли, по городу или региону также позволяет выявить новые возможности увеличения производства, изменения ассортимента производимой продукции и т.д.
Сопоставляя различные показатели одной и той же организации, можно выявить более (или менее) рентабельные виды продукции, отношение к данной организации ее контрагентов (например, через соотношение периода оборачиваемости дебиторской и кредиторской задолженности) и т.д.
Используя сравнение, различают:
- горизонтальный сравнительный анализ, который применяется для определения абсолютных и относительных отклонений фактического уровня исследуемых показателей от базового;
- вертикальный сравнительный анализ, используемый для изучения структуры итоговых экономических показателей, например, с целью выявления удельного веса отдельных видов активов организации в общей их сумме, принимаемой за 100%;
- трендовый анализ, применяемый при изучении темпов роста и прироста какого-либо показателя за ряд лег к уровню базисного периода (как правило, года), и определение основной тенденции динамики показателя;
- одномерный сравнительный анализ, который применяется для сопоставления одного или нескольких показателей одного объекта или нескольких объектов по единому показателю;
- многомерный сравнительный анализ, который заключается в сравнении результатов деятельности нескольких организаций по широкому кругу показателей.
Важным направлением сравнения является сопоставление результатов деятельности до и после применения того или иного мероприятия (изменения того или иного фактора) с целью определения количественного влияния фактора и определения резервов, например, влияние повышения цен реализации продукции на рентабельность капитала.
В каждом случае сравнение зависит от цели анализа и стоящих перед ним задач.
Рассмотрим наиболее типичные ситуации, в которых используется способ сравнения.
1. Выявление степени выполнения планов посредством сравнения соответствующих фактических показателей с плановыми (табл. 12.1).
Таблица 12.1
| Показатель | По плану | Фактически | Отклонение (+; -) | Процент выполнения плана |
|---|---|---|---|---|
| 1 | 2 | 3 = 2-1 | 4 = 2/1 × 100% | |
| Выручка, тыс. руб. | 97148 | 96324 | -824 | 99,2 |
| Прибыль от продаж, тыс. руб. | 11391 | 12052 | +661 | 105,8 |
Как видно из табл. 12.1, план прибыли выполнен на 105,8%, сверх плана получено 661 тыс. руб. прибыли. В то же время план по реализации продукции недовыполнен на 0,8% (99,2 - 100,0). В отчетном году было продано продукции на 824 тыс. руб. меньше, чем было установлено планом.
2. Сопоставление фактических показателей отчетного периода с соответствующими показателями предшествующего (прошлого или базисного) периода (табл. 12.2).
Таблица 12.2
| Наименование продукции | Базисный период | Отчетный период | Отклонение (+;-) | Темп роста, % |
|---|---|---|---|---|
| 1 | 2 | 3 = 2-1 | 4 = 2/1 × 100 | |
| А, ед. изделий | 328 | 344 | + 16 | 104,9 |
| Б, ед. изделий | 430 | 412 | -18 | 95,8 |
Данные таблицы 12.2 позволяют сделать следующие выводы. В отчетном периоде организации произвела продукции А больше, чем в базисном периоде на 16 единиц, или на 4,9%. Производство продукции Б уменьшилось по сравнению с базисным периодом на 18 единиц, или на 4,2% (95,8 - 100,0).
3. Сопоставление фактических показателей отчетного периода со средними значениями этих показателей за три-пять прошедших лет (табл. 12.3).
Таблица 12.3
| Наименование продукции | Выручка от реализации продукции за прошлые годы | В среднем за 5 лет | Отчетный год | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| А, тыс. руб. | 3390 | 3670 | 4120 | 4390 | 4864 | 4086,8 | 5178 |
| Б, тыс. руб. | 2570 | 2782 | 2658 | 2911 | 2860 | 2756,2 | 2750 |
Данные таблицы 12.3 свидетельствуют о том, что реализация продукции А развивается успешно, так как в отчетном году реализация превысила не только прошлогодний, но и среднегодовой уровень. Реализация продукции Б требует более глубокого изучения, поскольку в отчетном году объем продаж был не только менее, чем в прошлом году, но меньше среднегодовой продажи за последние пять лет.
4. Оценка резервов увеличения производства продукции осуществляется путем сравнения фактических данных об объеме производства за отчетный год с плановыми показателями, определенными с учетом организационно-технических мероприятий по увеличению производства продукции.
5. Сравнение одних экономических показателей с другими показателями деятельности организации (табл. 12.4).
Таблица 12.4
| Показатели | Прошлый год | Отчетный год | Отклонение (+; -) |
|---|---|---|---|
| Продолжительность оборота дебиторской задолженности, дни | 55 | 69 | + 14 |
| Продолжительность оборота кредиторской задолженности, дни | 78 | 53 | -25 |
| Соотношение оборачиваемости дебиторской и кредиторской задолженности | 0,7 | 1,3 | +0,6 |
Как видно из данных табл. 12.4, финансовое состояние организации несколько ухудшилось, так как продолжительность дебиторской задолженности возросла, а кредиторской — сократилась. Это может означать, что у организации возникли сложности с реализацией продукции (например, вследствие снижения спроса) и она вынуждена увеличивать срок коммерческого кредита для покупателей. При этом продолжительность кредиторской задолженности возросла, что может свидетельствовать о снижении доверия к организации со стороны поставщиков. Сравнивая изменение соотношения оборачиваемости дебиторской и кредиторской задолженности, можно прийти к тем же выводам, так как в динамике оно повысилось.
Обязательным условием применения метода сравнения должна быть сопоставимость сравниваемых показателей (плановых и отчетных показателей, показателей отчетного и прошлых периодов и т.п.), предполагающая:
- сравнимость объемных, стоимостных, качественных, структурных показателей;
- единство периодов времени, за которые производится сравнение;
- сопоставимость условий производства;
- сопоставимость методики расчета показателей.
Подчеркнем: сравнивать можно только качественно однородные величины.
Выявленные отклонения являются объектом дальнейшего анализа. При анализе отклонений от плановых значений целесообразно оцепить качество самого планирования. Так, например, значительные положительные отклонения от плана (перевыполнения плана) могут явиться результатом заниженного или недостаточно напряженного плана.
Группировка аналитической информации — деление изучаемой совокупности объектов на однородные группы по соответствующим признакам. Данный метод анализа часто является неотъемлемой составляющей аналитического исследования. Простой подсчет итогов, сравнение показателей не всегда позволяет достаточно полно оценить особенности деятельности организации, динамики ее показателей. Поэтому до осуществления расчетов проводят предварительную характеристику совокупности, ее группировку. Она позволяет изучить экономические явления и процессы во взаимосвязи, взаимозависимости, выявить наиболее существенные факторы, обнаружить те или иные тенденции и закономерности, свойственные этим явлениям и процессам. Группировки исходных данных широко применяются при анализе плановых и отчетных показателей. С их помощью можно показать зависимость уровня затрат от объема продаж, оборачиваемости и др. Без группировки нельзя узнать, за счет чего перевыполнен или недовыполнен план, как он выполняется разными типами организаций.
Объектами изучения выступают как сами хозяйствующие субъекты, так и их структурные подразделения, хозяйственные операции.
Группировка предполагает классификацию явлений и процессов, а также причин и факторов, их обусловливающих. Нельзя группировать явления по случайному признаку, необходимо сделать обоснованный выбор признаков. Одним из важнейших методологических принципов, лежащих в основе научного выбора группировочных признаков и построения группировок, является положение, согласно которому производить их следует с обязательным учетом качественных характеристик группируемых единиц совокупности. Эти характеристики должны учитывать сущностные (наиболее важные) признаки изучаемого явления, процесса или объекта, позволяя объединить в отдельные (самостоятельные) группы однородные по социально-экономической и правовой природе единицы изучаемой совокупности. Только продуманные группировки дают возможность глубоко проанализировать явления, характеризовать их черты, взаимосвязи между отдельными показателями.
Группировки подразделяются по сложности построения:
- простые (с помощью которых изучается взаимосвязь между объектами, структурированными по определенному признаку);
- комбинированные (сначала делятся по одному признаку, а потом внутри каждой подгруппы происходит деление по другим признакам).
В зависимости от целей анализа используют типологические, структурные и аналитические группировки.
В экономическом анализе структурные группировки широко используются при изучении состава хозяйствующих субъектов (но мощности, уровню автоматизации, величине основных фондов и т.д.).
Типологические группировки позволяют разграничить изучаемые совокупности на однородные группы, тины но существенному качественному признаку. Примером типологической группировки может быть группировка организаций по видам деятельности или по формам собственности. Типологическая группировка оформляется в таблицу, выделенные группы (на основе комбинации группировочных признаков) объединяются в намеченные типы и определяется численность (удельный вес) каждого из них.
Структурная группировка аналитической информации может производиться, чтобы изучить изменение структуры типически однородных групп явлений, процессов или объектов. Для структурной группировки необходимо наличие однородных совокупностей, расчленяемых по величине изменяющегося признака. Если в основе типологической группировки лежат качественные признаки, то в основу структурной положены количественные признаки изучаемой совокупности. Структурные группировки позволяют изучить внутреннее строение показателя и соотношение в нем отдельных частей. Например, с помощью структурной группировки можно изучить состав выпускаемой продукции по номенклатуре и ассортименту, состав рабочих по профессиям, стажу работы, по возрасту и т.д. В процессе аналитической работы можно сгруппировать подразделения организации по уровню выполнения плана, производительности труда, загрузке оборудования, оснащенности средствами автоматизации и механизации труда и др., чтобы определить уровень экономической эффективности отдельных подразделений организации, выявить резервы улучшения работы отстающих подразделений.
Аналитические группировки — это распределение по зависимости, взаимосвязи между двумя или несколькими разнородными группами явлений или их признаками. Аналитические группировки позволяют выявить взаимосвязи, взаимозависимости и взаимодействия изучаемых показателей, явлений, объектов. Они дают возможность выявить многие скрытые зависимости и взаимосвязи, что имеет значение для принятия управленческих решений и развития хозяйственной деятельности организации. Например, при изучении спроса покупателей на продукцию организации целесообразно сгруппировать покупателей по полу, возрасту, уровню доходов, месту жительства и другим признакам.
Способы табличного отражения аналитических данных являются наиболее рациональными и удобными для восприятия формами представления результатов анализа.
Результаты аналитической сводки и группировки, как правило, помещаются в аналитических таблицах, представляющих собой рациональное, наглядное, компактное и систематизированное изложение показателей, изучаемых в процессе экономического анализа.
Горизонтальные линии таблицы именуются строками, а вертикальные графами (столбцами, колонками). Каждая строка и графа имеют свое наименование (заголовок), соответствующее содержание показателей, помещенных в таблице, а таблица в целом имеет общее наименование, определяющее ее содержание.
Любая правильно составленная таблица содержит два основных элемента: подлежащее и сказуемое. Подлежащее — это объект изучения или перечень единиц совокупности (их групп), которые характеризуются в таблице. Сказуемое — это перечень показателей, которыми характеризуется подлежащее.
При разработке аналитических таблиц в процессе сводки и группировки показателей, используемых для проведения анализа, следует иметь в виду, чтобы таблица не должна быть простым сводом данных, размещенных в произвольном порядке. Каждая таблица должна заключать в себе аналитическое изложение результатов наблюдения, чтобы в последовательном ряду строк и граф развертывалась цифровая картина тех явлений, которые подлежат анализу.
Таблица должна быть оптимальной по своему размеру. С одной стороны, ей следует содержать все необходимые показатели, с другой — не быть перегруженной избыточной статистической информацией.
Таблица должна иметь четкое общее название, а также названия подлежащего и сказуемого, их групп и разделов. Таблицы без названий понимаются с трудом. Кроме того, в них должны быть указаны единицы измерения, территория, период времени и другие необходимые сведения, привязывающие таблицу к конкретному содержанию, объему данных, времени и пространству.
Строки подлежащего и графы сказуемого могут размещаться от частного к общему или наоборот. Итоговые показатели обычно помещаются в последней строке или графе. Однако, исходя из задач, решаемых таблицей, итоговые показатели могут быть приведены и в первой строке.
Если таблица большая, ее строки и графы могут нумероваться (обозначаться) порядковыми числами или буквами по алфавиту.
Все приводимые в таблице цифровые данные должны иметь одинаковую степень точности (целые числа, целые числа с десятыми или сотыми показателями), что облегчает восприятие информации, содержащейся в таблице.
При отсутствии данных за какой-то год или по какому-то параметру вместо соответствующих цифр обычно ставится многоточие или помета «нет данных». Если отсутствие каких-то данных является объективным фактом (например, отсутствие изменения какого-либо показателя), то вместо соответствующих данных ставится прочерк (тире).
Все сомнения и вопросы, которые могут возникнуть при чтении таблицы, должны быть раскрыты в примечаниях к ней.
Методы функционального факторного анализа
Важной составляющей экономического анализа является изучение и количественная оценка влияния факторов на величину исследуемых экономических показателей.
Под экономическим факторным анализом понимается раскрытие полного набора прямых, количественно измеримых факторов, оказывающих влияние на изменение результативного показателя и оценка их влияния.
По характеру взаимосвязи между показателями различают методы функционального (детерминированного) и стохастического факторного анализа.
Детерминированный (функциональный) факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер.
Основными отличиями этого способа анализа являются:
- построение детерминированной модели на основе логического анализа;
- наличие прямой или обратной функциональной связи между факторным и результативным показателями;
- невозможность разделения результатов влияния одновременно действующих факторов, которые не поддаются объединению в одной модели;
- изучение взаимосвязей в краткосрочном периоде.
Недостаток детерминированного факторного анализа состоит в том, что научно-технические факторы интенсификации производства не могут быть включены в модель прямых связей, а следовательно, их недоучет приведет к занижению или завышению отдельных результатов. Другим недостатком является то, что результаты расчетов будут зависеть от того, насколько логически и экономически обоснованно составлена модель зависимости, а от этого, в свою очередь, зависят выводы.
Различают четыре типа детерминированных моделей:
- мультипликативные;
- аддитивные;
- кратные;
- смешанные.
Мультипликативные модели в обобщенном виде могут быть представлены формулой
| Y= | n | xi = x1 × x2 × ... × xn |
| П | ||
| i=1 |
где Y — результативный показатель; П — произведение факторных показателей; x1, x2, ..., xn — факторы, влияние которых изучается в данной модели.
Примером мультипликативной модели является трехфакторная модель объема продаж:
В = Ч × Д × Пт,
где В — объем продаж (выручка от реализации продукции); Ч — среднесписочная численность работников; Д — количество рабочих дней в периоде; Пт — средняя выработка на одного работника.
Аддитивные модели представляют собой алгебраическую сумму факторных показателей и имеют вид:
| Y= | n | xi = x1 + x2 + ... + xn |
| Σ | ||
| i=1 |
где Y — результативный показатель; Σ — сумма факторных показателей; x1, x2, ..., xn — факторы, влияние которых изучается в данной модели.
К таким моделям, например, относятся выручка от реализации продукции организации как сумма продаж отдельных видов продукции, сумма как сумма условно-постоянных и условно-перемененных статей издержек и т.и.
Кратные модели представляют собой отношение факторных показателей и имеют вид:
| Y = | x1 |
| x2 |
где Y — результативный показатель; x1, x2 — факторы, влияние которых изучается в данной модели.
Примером кратной модели служит показатель оборачиваемости запасов товаров в количестве оборотов (коэффициент оборачиваемости):
| Коб = | В |
| З |
где В — выручка от реализации товаров за исследуемый период; З — средний запас товаров.
Смешанные (комбинированные) модели представляют собой комбинацию вышеперечисленных моделей и могут быть описаны с помощью специальных выражений:
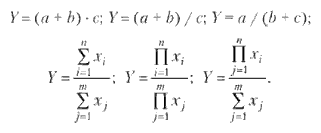
Примерами таких моделей служат показатели фондозатрат на 1 руб. произведенной продукции, показатели рентабельности и др.
Для более глубоко изучения зависимости между показателями и количественного измерения множества факторов, повлиявших на результативный показатель, можно использовать преобразования моделей с целью включения новых факторных показателей.
Для детализации обобщающего факторного показателя на его составляющие, которые представляют интерес для аналитических расчетов, используют прием удлинения, расширения, сокращения факторной системы (эти приемы рассмотрены в параграфе 10.6).
Детализация факторного анализа во многом определяется числом факторов, влияние которых можно оценить количественно, поэтому большое значение в анализе имеют многофакторные модели. В основе их построения лежат следующие принципы:
- место каждого фактора в модели должно соответствовать его роли в формировании результативного показателя;
- модель должна строиться из полной двухфакторной модели путем последовательного расчленения факторов, как правило, качественных, на составляющие;
- при написании формулы многофакторной модели факторы должны располагаться слева направо в порядке их замены.
Построение факторной модели — первый этап детерминированного анализа. Далее определяют способ оценки влияния факторов.
Индексный метод основывается на относительных показателях, выражающих отношение уровня данного явления к его уровню, взятому в качестве базы сравнения (к уровню его в прошлое время или к уровню аналогичного явления, принятому в качестве базы).
Используют несколько видов индексов, которые применяются при анализе: агрегатные, арифметические, гармонические и т.д. Выделяют индивидуальные и агрегатные (групповые) индексы. Индексы, выражающие соотношение непосредственно соизмеряемых величин, называются индивидуальными, а характеризующие соотношения сложных явлений — агрегатными (групповыми). Индивидуальные индексы рассчитываются по показателям, но которым не составляют факторные модели. Например, цена (р), себестоимость (с), объем (q).
Данный метод используется в мультипликативных и кратных моделях.
Используя агрегатную формулу индексов и соблюдая установленную вычислительную процедуру, можно определить влияние факторов на изменение результативного показателя. Алгоритм расчета следующий:
Σx1y1 - Σx0y0 = (Σx1y1 - Σx0y1) + (Σx0y1 - Σx0y0)
где х — количественный фактор; у — качественный фактор; Jxy = Σx1y1 / Σx0y0 — индекс изменения результирующего показателя; Jx = Σx1y0 / Σx0y0 — влияние количественного фактора; Jy = Σx0y1 / Σx0y0 - влияние качественного фактора.
Рассчитав индексы и построив временной ряд, характеризующий, например, выпуск продукции в стоимостном выражении, можно квалифицированно судить о динамике объема производства.
Пример 12.1
Оборот торговой организации в отчетном году составил 78300 тыс. руб., в прошлом — 64100 тыс. руб. Цены в отчетном году возросли в среднем на 18%. Необходимо определить:
- изменение стоимостного объема оборота в отчетном году;
- влияние на изменение оборота фактора цен;
- влияние на изменение оборота физического объема оборота (количества проданных товаров);
- долю прироста оборота за счет изменения цен и физического объема оборота.
Решение.
1. Исходя из условия, можно построить мультипликативную модель развития оборота в отчетном году под влиянием фактора цен и фактора физического объема оборота: Ipq = Iр × Iq.
2. Используя агрегатную форму индексов, полученную модель можно преобразовать следующим образом:
| Σp1q1 | = | Σp1q1 | × | Σp0q1 |
| Σp0q0 | Σp0q1 | Σp0q0 |
где Σp1q1 — оборот отчетного года; Σp0q0 — оборот прошлого года; Σp0q1 - оборот отчетного года в ценах прошлого года (оборот в сопоставимых ценах).
Отсюда схема расчетов факторов примет вид:
Σp1q1 - Σp0q0 = (Σp1q1 - Σp1q0) + (Σp1q0 - Σp0q0) или ΔΣpq = ΔΣpqp + ΔΣpqq.
где (Σp1q0 - Σp0q0), ΔΣpqp - влияние цен; (Σp1q1 - Σp1q0), ΔΣpqq - влияние количества.
3. Поскольку цены в отчетном году возросли на 18%, то индекс цен: Iр = 1,18.
4. Оборот в сопоставимых ценах составит: Σp0q1 = Σp1q1/ Iр = 78300 / 1,18 = 66356 тыс. руб.
5. Рассчитаем индекс физического объема оборота торговой организации:
Iq = Σp0q1 / Σp0q0 = 66 356 / 64 500 = 1,03.
6. Изменение стоимостного объема оборота организации (ΔΣpq) можно рассчитать путем вычитания из числителя первой дроби, входящей в модель, ее знаменатель:
ΔΣpq = Σp1q1 - Σp0q0 = 78300 - 64500 = 13800 тыс. руб.
Это изменение получено в результате совокупного влияния двух факторов: фактора цен и фактора количества проданных товаров.
7. Чтобы выявить влияние фактора цен на изменение оборота организации (ΔΣpqp), следует из числителя второй дроби, включенной в модель, вычесть ее знаменатель:
ΔΣpqp = Σp1q1 - Σp0q1 = 78300 - 66 356 = +11944 тыс. руб.
Таким образом, за счет повышения цен в среднем на 18% торговая организация получила дополнительную выручку в сумме 11944 тыс. руб.
8. Чтобы выявить влияние фактора физического объема оборота на изменение оборота организации (ΔΣpqq), следует из числителя третьей дроби, включенной в модель, вычесть ее знаменатель:
ΔΣpqq = Σp0q1 - Σp0q0 = 66 356 - 64 500 = +1856 тыс. руб.
Таким образом, за счет увеличения количества проданных товаров на 3% торговая организация получила дополнительную выручку в сумме 1856 тыс. руб.
9. Проверим правильность расчетов:
ΔΣpq = ΔΣpqp + ΔΣpqq = 11944 + 1856 = +13800 тыс. руб.
10. Рассчитаем долю прироста оборота за счет изменения:
а) цен: Дp = ΔΣpqp / ΔΣpq × 100 = +11944 / 13800 × 100 = 85,6%;
б) физического объема оборота: Дq = ΔΣpqq / ΔΣpq × 100 = 1856 / 13800 × 100 = 13,4%.
Следовательно, в отчетном году увеличение оборота торговой организации было получено, преимущественно, за счет повышения цен на реализуемые товары.
Элиминирование — это логический прием, при котором последовательно выделяется влияние одного фактора и исключается действие всех остальных. Иначе говоря, элиминировать — это значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме того, влияние которого оценивается количественно. При этом исходят из того, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все другие остаются без изменения, потом изменяется второй при неизменности остальных и т.д.
Применяются следующие методы элиминирования: метод разниц, метод цепной подстановки и интегральный метод.
Способ абсолютных разниц используют только в мультипликативных и смешанных моделях. При его использовании предварительно определяется абсолютная разница по изучаемым факторам. Затем отклонение (разница) по одному фактору умножается на абсолютное значение другого фактора. При этом сначала рассчитывается влияние экстенсивного фактора, а затем интенсивного.
Любой результирующий показатель, характеризующий хозяйственную деятельность организации, может быть получен либо за счет увеличения ресурсов (экстенсивным путем), либо за счет повышения эффективности использования имеющихся ресурсов без дополнительного их привлечения (интенсивным путем). Однако, как правило, получение результата достигается и тем и другим путем одновременно. Поэтому полученный результат может быть описан следующей моделью:
Р = Э × И,
где Р — результирующий показатель; Э — экстенсивный фактор; И — интенсивный фактор.
Отсюда, чтобы рассчитать влияние экстенсивного фактора, нужно изменение его величины умножить на величину интенсивного фактора в базисном периоде:
ΔРэ = (Э1 - Э0) × И0 = ΔЭ × И0,
где ΔРэ — изменение результата за счет влияния экстенсивного фактора; Э0, Э1 — значения экстенсивного фактора в базисном и отчетном периодах соответственно; И0 — величина интенсивного фактора в базисном периоде.
Для того чтобы рассчитать влияние интенсивного фактора, нужно изменение его величины умножить на величину экстенсивного фактора в отчетном периоде, но в отчетном периоде будет повышена интенсивность использования имеющихся ресурсов:
ΔРи = (И1 - И0) × Э1 = ΔИ × Э1,
где ΔРи — изменение результата за счет влияния интенсивного фактора; И0, И1 — значения интенсивного фактора в базисном и отчетном периодах соответственно; Э1 — величина экстенсивного фактора в отчетном периоде.
Пример 12.2
Необходимо рассчитать методом абсолютных разниц влияние на изменение оборота розничной торговли торговой организации фактора изменения торговой площади и фактора изменения объема оборота розничной торговли на 1м2 торговой площади.
Для расчетов используем данные табл. 12.5.
Как видно из табл. 12.5, в отчетном году оборот розничной торговли увеличился на 30335 тыс. руб. Это увеличение обусловлено влиянием экстенсивного и интенсивного факторов. Экстенсивным фактором является торговая площадь, а интенсивным — оборот на 1 м2 торговой площади. Для расчета влияния этих факторов можно использовать способ разниц. Сначала нужно написать модель связи результата с факторами. Поэтому обозначим оборот торговой организации буквой В (выручка), экстенсивный фактор буквой S, а интенсивный фактор буквой Р (реализация). При этом нужно помнить, что буквы для обозначения результата и факторов выбираются исходя из удобства пользователя, никаких общепринятых обозначений в данном случае не установлено.
Таблица 12.5
| Показатель | Условные обозначения | Базисный год | Отчетный год | Отклонение (+; -) | Темп роста, % |
|---|---|---|---|---|---|
| Оборот розничной торговли, тыс. руб. | В | 89900 | 120235 | +30335 | 133,7430 |
| Торговая площадь, м2 | 5 | 950 | 1150 | +200 | 121,0526 |
| Оборот розничной торговли на 1 м2 торговой площади, тыс. руб. | Р | 94,6316 | 104,5522 | +9,9206 | 110,4834 |
Итак, модель связи будет иметь вид: В = S × Р.
Теперь можно рассчитать влияние факторов.
1. Фактор изменения торговой площади (экстенсивный):
ΔBs = ΔS × Р0 = +200 × 94,6316 = + 18926 тыс. руб.
2. Фактор изменения оборота розничной торговли на 1 кв. м. торговой площади:
ΔВр = ΔР × S1 = +9,9206 × 1150 = +11409 тыс. руб.
Сумма влияния факторов:
ΔВ = ΔВs + ΔВр = (+18926) + (+11409) = +30335 тыс. руб.
Как видно из таблицы и проведенных расчетов, в отчетном году оборот розничной торговли торговой организации увеличился на 30335 тыс. руб. Это произошло, прежде всего, за счет увеличения торговой площади. Увеличение торговой площади на 200 м2 позволило увеличить выручку организации на 18926 тыс. руб. Положительным является и то, что в отчетном году повысилась эффективность использования торговой площади. Увеличение оборота в расчете на каждый квадратный метр торговой площади позволило увеличить оборот торговой организации на 11409 тыс. руб.
В то же время следует отметить, что оборот торговой организации развивался преимущественно экстенсивным путем.
Если в модели, приведенной в примере, поменять местами экстенсивный и интенсивный факторы, то результаты расчетов будут иными. Это означает, что порядок замены в мультипликативной модели крайне важен для интерпретации полученных результатов.
Поэтому, прежде чем приступить к расчетам, необходимо:
- выявить четкую взаимосвязь между изучаемыми показателями;
- четко определить экстенсивные (количественные) и интенсивные (качественные) показатели;
- правильно определить последовательность подстановок.
Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных моделях.
Расчет влияния факторов осуществляется следующим образом.
Для расчета влияния первого фактора необходимо базисную величину результативного показателя умножить на относительный прирост первого фактора, выраженного в процентах (темп прироста), и результат разделить на 100%.
Изменение результата за счет экстенсивного фактора (ΔРэ):
ΔРэ = (Р0 × ΔЭ%) / 100%;
ΔЭ% = (Э1 - Э0)/Э0 × 100%.
Чтобы рассчитать влияние интенсивного фактора, необходимо к базисной величине результативного показателя прибавить изменение результативного показателя за счет первого фактора и затем полученную сумму умножить на относительный прирост интенсивного фактора в процентах и результат разделить на 100%.
Изменение результата за счет интенсивного фактора (ΔРи):
ΔРи = (Р0 + ΔРэ) × ΔИ% / 100%;
ΔИ% = (И1 - И0) / И0 × 100%.
Пример 12.3
Проведем расчеты по данным предыдущего примера из табл. 12.5.
1. Фактор изменения торговой площади (экстенсивный):
ΔВs = (В0 × ΔS%) / 100% = 89900 × 21,0526 / 100 = + 18926 тыс. руб.
2. Фактор изменения оборота розничной торговли на 1 м2 торговой площади:
ΔВр = (В0 + ΔВs) × ΔИ% / 100% = (89900 + 18926) × 10,4834 / 100 = = +11409 тыс. руб.
Сумма влияния факторов:
ΔВ = ΔВs + ΔВр = (+18926) + (+11409) = +30335 тыс. руб.
Метод относительных разниц можно применять и в том случае, если число изучаемых факторов более двух. При этом влияние третьего, четвертого и т.д. факторов (при их наличии) определяется аналогично расчету второго фактора с добавлением в сумму изменения результата за счет влияния второго, третьего и т.д. факторов.
Данный способ очень эффективен в тех случаях, когда исходные данные содержат относительные изменения факторных показателей в процентах или коэффициентах (индексах). Его удобно применять в тех случаях, когда требуется рассчитать влияние большого количества факторов.
Метод цепной подстановки. Сущность данного приема экономического анализа заключается в последовательном элиминировании одних факторов для определения влияния других, т.е. в последовательной замене базисной величины факторных показателей, входящих в модель зависимости (расчетную формулу), фактической величиной (величиной отчетного периода) этих показателей. После каждой замены результат подсчета сравнивают с результатом, полученным до замены этого показателя в данной формуле. Рассчитанные отклонения отражают влияние каждого фактора.
Если показатель является произведением трех сомножителей (факторов), то формула для базисного показателя будет следующей:
Y0 = а0 × b0 × с0,
а для фактического показателя:
Y1 = а1 × b1 × с1.
Изменение результативного показателя, с одной стороны, можно представить как разность между фактической и базисной его величиной, а с другой стороны, как сумму изменений результативного показателя под влиянием отдельных факторов:
Y1 - Y0 = ΔY = ΔYa + ΔYb + ΔYc.
Для определения влияния каждого из трех факторов необходимо произвести следующие расчеты.
Сначала рассчитывается влияние фактора а. Для этого в базисной модели заменяем базисное значение данного фактора на его фактическое значение:
Y2 = а1 × b0 × с0;
Y0 = а0 × b0 × с0.
Данные расчетные формулы отличаются лишь значением фактора а, величина остальных факторов не изменяется. Поэтому, если из полученного условного показателя (Y2) вычесть базисный (Y0), то полученный результат и покажет влияние первого фактора на изменение результирующего показателя:
Y2 - Y0 = ΔYa.
Затем последовательно, т.е. справа налево, в формуле Y2 заменим базисную величину следующего фактора (фактора «b») на его фактическое значение и получим следующий условный показатель Y3. Он отличается от Y2 лишь величиной фактора «b»:
Y3 = а1 × b1 × с0;
Y2 = а1 × b0 × с0.
Отсюда влияние фактора b можно рассчитать, сравнив Y3 с Y2:
Y3 - Y2 = ΔYb.
В следующей формуле заменим базисное значение фактора с на фактическое и получим формулу Y1, которая отличается от Y3 лишь на величину фактора с:
Y1 = а1 × b1 × с1;
Y2 = а1 × b0 × с0.
Отсюда влияние фактора «с» можно рассчитать, сравнив Y1 с Y3:
Y1 - Y3 = ΔYc.
Пример 12.4
Рассчитать методом цепной подстановки влияние следующих факторов на изменение оборота розничной торговли торговой организации в отчетном году но сравнению с прошлым годом:
- фактор изменения торговой площади;
- фактор изменения количества рабочих дней;
- фактор изменения объема среднедневного оборота розничной торговли на 1м2 торговой площади.
Для расчетов используем данные табл. 12.6.
Таблица 12.6
| Показатели | Условные обозначения | Базисный год | Отчетный год | Отклонение (+; -) |
|---|---|---|---|---|
| Оборот розничной торговли, тыс. руб. | В | 89900 | 120235 | +30335 |
| Торговая площадь магазинов, м2 | S | 950 | 1150 | +200 |
| Количество рабочих дней | Д | 310 | 305 | -5 |
| Среднедневной оборот розничной торговли на 1 м2 торговой площади, тыс. руб. | P | 0,3053 | 0,3428 | +0,0375 |
Сначала необходимо написать модель взаимосвязи между результативным и факторными показателями. Она будет иметь следующий вид:
В = S × Д × Р.
Следовательно, модель расчета оборота розничной торговли имеет вид:
- в базисном году: В0 = S0 × Д0 × Р0;
- в отчетном году: В1 = S1 × Д1 × Р1.
Из полученных моделей видно, что на развитие оборота розничной торговли в отчетном году оказали влияние три фактора.
Рассчитаем влияние каждого фактора в отдельности. Для расчета и количественной оценки влияния факторов используем способ цепной подстановки.
1. Базисное значение оборота розничной торговли исследуемой организации можно рассчитать по формуле В0 = S0 × Д0 × Р0. Как видно из табл. 12.6, его значение составило 89900 тыс. руб.
2. Затем в данной формуле заменим S0 на S1 и получим величину оборота розничной торговли при условии, что площадь будет отчетного года, а количество рабочих дней и среднедневной оборот розничной торговли на 1 м2 торговой площади — базисного:
В2 = S1 × Д0 × Р0 = 1150 × 310 × 0,3053 = 108826 тыс. руб.
Отсюда влияние фактора торговой площади составит:
ΔВs = В2 - В0 = S1 × Д0 × Р0 - S0 × Д0 × Р0 = (S1 - S0) × Д0 × Р0 = 108826 — 89900 = +18926 тыс. руб.
Таким образом, можно сделать вывод о том, что фактор торговой площади оказал положительное влияние на изменение оборота торговой организации, так как за счет приращения площади на 200 м2 создал предпосылки для увеличения оборота на 18926 тыс. руб.
3. Далее продолжим последовательно заменять базисные значения факторов на их фактическое значение в отчетном году.
В формуле В2 заменим Д0 на Д1 и получим условную величину оборота розничной торговли исходя из того, что площадь и количество рабочих дней будут теми же, что и в отчетном году, а среднедневной оборот розничной торговли на 1 м2 торговой площади — таким же как в базисном:
В3 = S1 × Д1 × Р0 = 1150 × 305 × 0,3053 = 107071 тыс. руб.
Отсюда влияние фактора количества рабочих дней составит:
ΔВД = В3 - В2 = S1 × Д1 × Р0 - S1 × Д0 × Р0 = S1 × (Д1 - Д0) × Р0 = 107071 - 108826 = -1755 тыс. руб.
Как видно из расчета, сокращение числа рабочих дней в отчетном периоде, по сравнению с базисным, на 5 дней создало предпосылки к уменьшению оборота торговой организации на 1755 тыс. руб.
4. Затем в формуле В3 заменим Р0 на Р1 и получим фактический оборот розничной торговли в отчетном году: В1 = S1 × Д1 × Р1.
Данные о величине этого оборота можно взять из табл. 12.6. Фактический оборот торговой организации в отчетном году составил 120235 тыс. руб.
Отсюда влияние фактора среднедневного оборота розничной торговли на 1 м2 торговой площади составит:
ΔВp = В1 - В3 = S1 × Д1 × Р1 - S1 × Д1 × Р0 = S1 × Д1 × (P1 - P0) = 120235 - 107071 = +13164 тыс. руб.
Таким образом, из табл. 12.6 видно, что в отчетном году повысилась эффективность использования торговой площади. Если в базисном году среднедневной оборот, получаемый торговой организацией с каждого квадратного метра торговой площади, составлял 0,3053 гыс. руб., то в отчетном году — 0,3428 тыс. руб. Увеличение оборота с одного квадратного метра торговой площади в среднем за день на 0,0375 тыс. руб.
5. Совокупное влияние факторов:
ΔВ = ΔВs + ΔВд + ΔВр = (+18926) + (-1755) + (+13164) = +30335 тыс. руб., что соответствует данным табл. 12.6.
Следует заметить, что данный способ анализа используется, лишь когда зависимость между изучаемыми явлениями представляется в виде прямой или обратно пропорциональной зависимости. В этих случаях анализируемый совокупный показатель как функция нескольких переменных должен быть изображен в виде произведения или частного от деления одних показателей на другие.
Преимущества данного способа — универсальность применения, простота расчетов.
Недостаток приема цепной подстановки состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора или распределяется между влиянием всех качественных факторов. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Однако существуют правила, определяющие последовательность подстановки:
- при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается влияние количественных факторов;
- если модель представлена несколькими количественными и качественными показателями, последовательность подстановки определяется путем логического анализа.
Например, годовой объем производства продукции (В) на оборудовании i-й группы может рассматриваться как произведение количества единиц оборудования (Кi) и годовой производительности единицы оборудования (ГПi), т.с. быть описан моделью следующего вида:
В = Кi × ГПi,
где Кi — экстенсивный (количественный) фактор; ГПi — интенсивный (качественный) фактор.
В свою очередь, годовая производительность единицы оборудования зависит от количества рабочих дней (Д) и суточной производительности единицы оборудования ДПi, где первый фактор также будет экстенсивным, а второй — интенсивным. Отсюда исходная модель примет вид:
В = Кi × Д × ДПi.
Суточную производительность также можно рассмотреть как произведение экстенсивного фактора — коэффициента сменности (Ксм), и интенсивного фактора сменной производительности СПi. Следовательно, годовой объем производства продукции может быть описан моделью:
В = Кi × Д × Ксм × СПi
и т.д.
Балансовый метод экономического анализа применяют при исследовании влияния факторов на определенный результативный показатель, при условии, что все они взаимоувязаны в балансовой формуле. Метод состоит в сравнении, соизмерении двух комплексов показателей, стремящихся к определенному равновесию. Он позволяет выявить в результате новый аналитический (балансирующий) показатель. Балансовая увязка различных показателей нужна для изучения отдельных сторон хозяйственной деятельности организаций. С помощью этого приема анализируют соотношение наличия и поступления товарных фондов с их использованием и т.д.
Например, товарный баланс имеет формулу
Зн + П = Р + В + Зк,
где Зн и Зк — запасы товаров на начало и конец исследуемого периода; П — поступление товаров; В — прочее выбытие товаров (естественная убыль, порча, возврат товаров поставщикам и т.п.); Р — объем реализации товаров (выручка).
На основе модели товарного баланса можно выявить влияние факторов на объем реализации товаров в натуральном или стоимостном выражении. Для этого на основе модели товарного баланса сначала рассчитывают реализацию товаров в отчетном периоде, затем — в базисном периоде, а затем рассчитывают разность по каждому элементу товарного баланса:
Р1 × (Зн1 + П1 - В1 - Зк1) - Р0 × (3н0 + П0 - В0 - Зк0) = ΔР = ΔЗн + ΔП - ΔВ - ΔЗк.
Таким образом, из модели, характеризующей изменение результирующего и факторных показателей, можно сразу увидеть не только изменение результата хозяйственной деятельности организации, но и влияние на него каждого из изучаемых факторов.
Пример 12.5
Данные табл. 12.7 характеризуют элементы товарного баланса торговой организации в прошлом и отчетном периодах.
Таблица 12.7
| Показатель, тыс. руб. | Прошлый период | Отчетный период | Отклонение (+,-) |
|---|---|---|---|
| Запасы товаров на начало периода | 5344 | 5149 | -195 |
| Поступление товаров | 71842 | 74578 | 2736 |
| Прочее выбытие | 630 | 520 | -110 |
| Запасы товаров на конец года | 5149 | 5343 | 194 |
| Оборот розничной торговли | 71407 | 73864 | 2457 |
Необходимо:
- методом балансовой увязки рассчитать влияние факторов на изменение объема продажи товаров в отчетном периоде по сравнению с прошлым годом;
- проанализировать результаты.
Как видно из табл. 12.7, влияние факторов на изменение оборота розничной торговли торговой организации рассчитано методом сравнения, что приводит к неверной оценке влияния ряда факторов (прочее выбытие, запасы товаров на конец года). Поэтому лучше воспользоваться балансовым методом (суммы в тыс. руб.):
73864 (5149 + 74578 - 520 - 5343) - 71401 (5344 + 71842 - 630 -5149) = +2457 = (-195) + (+2736) - (-100) - (+194)
или
+2457 = -195 + 2736 + 100 - 194.
Из проведенных расчетов видно истинное влияние факторов. Оборот розничной торговли увеличился под влиянием увеличения поступления товаров и снижением прочего выбытия товаров, отрицательное влияние на динамику оборота оказало снижение запасов товаров на начало периода и их увеличение на конец периода.
При использовании балансового метода в процессе экономического анализа обеспеченности организации сырьем сравнивают потребность в сырье, источники покрытия потребности и определяют балансирующий показатель — дефицит или избыток сырья. С помощью данного метода анализируется использование рабочего времени (баланс рабочего времени), использование производственной мощности (баланс производственной мощности), баланс трудовых ресурсов и т.д.
Как вспомогательный, балансовый метод используется для проверки результатов расчетов влияния факторов на результативный совокупный показатель. Если сумма влияния факторов на результативный показатель равна его отклонению от базового значения, то, следовательно, расчеты проведены правильно. Отсутствие равенства свидетельствует о неполном учете факторов или о допущенных ошибках:
| ΔY = | n | ΔY(xi) |
| Σ | ||
| i=1 |
где ΔY — изменение результативного показателя; xi — факторы; ΔY(xi) — изменение результативного показателя за счет фактора xi.
Балансовый метод применяют также для определения размера влияния отдельных факторов на изменение результативного показателя, если известно влияние остальных факторов.
Балансовый прием анализа может применяться при изучении финансового положения организации. С его помощью на основе бухгалтерского баланса сопоставляют данные пассива (источники средств) с данными актива (состав и размещение средств), устанавливают правильность использования средств, банковских кредитов и т.д.
Интегральный способ. Недостатком способа разниц и способа цепной подстановки, как уже говорилось, является то, что результаты расчетов зависят от последовательности замены факторов и неразложимый остаток часто необоснованно приписывается влиянию изменения качественного фактора. Этот недостаток устраняется при использовании интегрального метода. Он не требует применения приемов но распределению неразложимого остатка но факторам, так как в нем действует логарифмический закон перераспределения факторных нагрузок. Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т.е. применим к мультипликативным, кратным и смешанным моделям. Операция вычисления определенного интеграла сводится к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы.
Данный метод объективен, поскольку исключает какие-либо предположения о роли факторов до проведения анализа, соблюдается положение о независимости факторов.
Использование этого способа позволяет получить более точные результаты расчетов, не зависящие от расположения факторов: изменение результативного фактора пропорционально раскладывается между факторами.
Если изучается влияние на результативный показатель двух факторов, то для расчета можно использовать формулу:
Y = a × b.
Расчет влияния факторов осуществляется по формулам:
ΔYa = b0 × Δа + (Δа × Δb)/2;
ΔYb = a0 × Δb + (Δa × Δb)/2.
Неформализованные методы экономического анализа
Под экспертной диагностикой понимаются средства анализа, основанные на обобщении оценок и информации, данной экспертами. Этот метод применяют, когда необходимо выбрать решение, которое не может быть определено на основе точных расчетов. Такие ситуации часто возникают в разработках современных проблем управления производством и, главное, при прогнозировании и долгосрочном планировании. Сущность метода экспертных оценок заключается в проведении экспертами интуитивно-логического анализа проблемы с количественной оценкой суждений и формальной обработкой результатов. Получаемое в результате обработки обобщенное мнение экспертов принимается как один из вариантов решения стоящих перед организацией задач. Комплексное использование интуиции (неосознанного мышления), логического мышления и количественных оценок с их формальной обработкой позволяет получить эффективное решение проблемы.
Таким образом, данный метод анализа строится на информации, получаемой часто контактными методами посредством проведения специальных экспертных опросов и полученных на их основе экспертных оценок.
Экспертные оценки — это количественные или порядковые оценки процессов или явлений, не поддающиеся непосредственному измерению. Они основываются на суждениях специалистов. В принципе, поэтому их нельзя считать вполне объективными, так как на специалиста-эксперта могут воздействовать различные побочные факторы. В то же время активное и целенаправленное участие специалистов в каждом этапе принятия управленческих решений позволяет повысить их качество и эффективность.
В процессе проведения анализа экспертами используют анкетные методы и методы групповой экспертизы.
Достоинствами этих методов являются простота организации, возможность применения статистической обработки данных, возможность охвата больших групп информации.
Среди недостатков можно выделить неполноту ответов, субъективный фактор опрашиваемых, возможность неправильного понимания вопросов экспертами.
Для обработки субъективных мнений экспертов применяются различные приемы, основным из которых является ранжирование.
Ранжирование предполагает упорядочивание оцениваемых объектов в порядке возрастания или убывания их качеств. Ранжирование может осуществляться несколькими методами, но в основе каждого из них лежат экспертные мнения — суждения специалистов об оцениваемом объекте.
Наиболее распространенным методом проведения ранжирования является мягкая рейтинговая оценка. Согласно этому методу эксперты оставляют в списке, не указывая приоритет, наилучшие, с их точки зрения, оцениваемые объекты. Наивысший ранг получает объект, набравший большее число голосов экспертов.
Другим способом проведения рейтинговой оценки является непосредственное ранжирование. Сущность этого метода состоит в том, что эксперты располагают в определенном порядке (как правило, возрастания или убывания качеств) оцениваемые объекты, затем рассчитывается среднее арифметическое место каждого объекта и в соответствии с этим значением составляется окончательно упорядоченный список. Достоверность результатов экспертизы проверяется но значению коэффициента конкордации — согласованности методов экспертов.
Более сложным методом ранжирования является попарное сравнение, в соответствии с которым эксперты, сопоставляя поочередно каждые два оцениваемых объекта, определяют, какой из них лучше, затем эти мнения усредняются и составляется окончательный рейтинг по правилу: «Если А лучше В, В лучше С, то А лучше С». Проблема применения этого способа связана с тем, что экспертам приходится анализировать большое число пар, при этом усреднение может привести к логическому тупику: «А лучше В, В лучше С, С лучше А». Кроме того, непосредственное ранжирование невозможно применить, если список оцениваемых объектов остается открытым.
При использовании метода ранжирования на основе балльной оценки список оцениваемых объектов может быть неограничен. Эксперты сами называют число объектов и оценивают их в баллах или располагают их в определенном порядке, при этом порядковому номеру присваивается соответствующее число баллов. Для получения окончательно упорядоченного списка ранжируемых объектов баллы складываются, а объекты располагаются в порядке возрастания или убывания баллов.
Главная проблема ранжирования как одного из методов оценки связана с тем, что сравнения объектов осуществляются по нескольким показателям и результаты могут быть неоднозначными: лидер по одному показателю может стать аутсайдером по другому (классический пример: высокая доходность корпоративных ценных бумаг при высокой степени риска инвестиций).
Поэтому встречается рейтинг, в котором объекты ранжированы отдельно по каждому показателю. Право определить, какое из ранжированных качеств является наиболее важным, предоставляется тому, кто использует результаты рейтинга. Также предпринимаются попытки согласования ранжированных списков на базе элементарных методов расчета средневзвешенных величин с учетом коэффициентов весомости (важности для анализа) показателей или специального математического и логического аппарата.
Использование результатов рейтинга значительно упрощает аналитическую работу по оценке сложившейся ситуации и выработке управленческого решения.
Разновидностями метода экспертных оценок являются:
- метод «мозговой атаки» (возникновение идей происходит в творческом споре и личном контакте специалистов);
- метод «мозгового штурма» (когда одна группа экспертов выдвигает идею, а другая ее анализирует);
- метод «дельфи» (предусматривает анонимный опрос специалиста по заранее подготовленным вопросам с последующей обработкой ответов).
Процесс разработки управленческих решений зависит от уровня информационного обеспечения, умения анализировать полученные данные и синтезировать на их основе варианты возможных решений. Ситуационный подход позволяет осуществлять эффективное управление конкретной ситуацией принятия управленческого решения.
Ситуационный анализ — это комплексный процесс, позволяющий обосновать принятие и управленческого решения, в основе которого лежит анализ отдельно взятой управленческой ситуации. В процессе ситуационного анализа используется метод индукции, анализ начинается с изучения конкретных ситуаций, проблем, возникающих в деятельности организации, по которым должно быть принято управленческое решение.
Ситуационный анализ позволяет, основываясь на более глубоком исследовании ситуаций, установлении тенденций, закономерностей и факторов, определяющих их развитие, обосновывать стратегические управленческие решения вплоть до корректировки стратегических целей организации.
Одной из основных проблем, решаемых ситуационным анализом, является установление факторов, определяющих развитие ситуации. При этом важным является установление не всех, а именно основных факторов, оказывающих существенное влияние на развитие ситуации, и отбрасывание тех факторов, которые существенного влияния оказать не могут.
Для выявления основных факторов в процессе анализа той или иной конкретной ситуации применяются различные приемы, среди которых можно выделить:
- метод «мозговой атаки»;
- метод двухтурового анкетирования.
«Мозговая атака» в ситуационном анализе, как правило, проводится в два этапа: на первом этапе происходит генерирование идей, а на втором — обсуждение выявленных идей, их оценка и выработка коллективной точки зрения. Па втором этапе может быть использован так называемый метод суда: участвующие в проведении анализа эксперты делятся на сторонников и противников высказанного мнения.
Двухтуровое анкетирование предполагает индивидуальную работу специалистов по выявлению наиболее важных, основных факторов, определяющих развитие ситуации. В первом туре каждый из специалистов заполняет специально разработанную анкету, в которой указывает основные факторы и обосновывает причины отнесения этих факторов к основным. Внесенные в анкету факторы ранжируются специалистом по степени их влияния на развитие ситуации. Во втором туре проводится перекрестное рецензирование заполненных в первом туре анкет. Это означает, что анкеты, заполненные одним специалистом, оценивают другие и соглашаются либо не соглашаются со сделанными им оценками. Результаты второго тура обрабатываются аналитической группой, формирующей на основании данных, представленных в анкетах, перечень факторов, по мнению специалистов определяющих развитие ситуации.
В ситуационном анализе могут быть использованы различные методы моделирования:
- аналоговые модели, с помощью которых моделируется, например, организационная структура и прохождение команд;
- математические модели, позволяющие отслеживать развитие ситуации с помощью установления точных зависимостей, например зависимости между объемами производства и издержками.
С их помощью могут решаться задачи распределения ресурсов при стратегическом управлении и многие другие задачи; модели теории игр и др.
Проводя ситуационный анализ и принимая на его основании управленческие решения, невозможно однозначно определить направление, по которому пойдет развитие ситуации. Однако он позволяет предусмотреть наиболее вероятные сценарии развития ситуации, подготовить наиболее предпочтительные альтернативные варианты решений в каждом из возможных направлений развития ситуации. Сценарий — преимущественно качественное описание возможных вариантов развития исследуемого объекта при различных сочетаниях определенных, заранее выделенных условий. Метод сценария не предназначен для прогноза, он лишь должен в развернутой форме показать возможные варианты развития событий для их дальнейшего анализа и выбора наиболее реального.
Методы ситуационного и сценарного анализа тесно взаимосвязаны с методом SWOT-анализа.
SWOT — это акроним слов Strengts (силы), Weaknesses (слабости), Opportunities (благоприятные возможности) и Threats (угрозы). Внутренняя обстановка фирмы отражается в основном в S и W, а внешняя — в О и Т. Метод 5№ОГ-анализа позволяет, с одной стороны, выявить внутренние сильные и слабые стороны деятельности организации, а с другой стороны — внешние возможности и угрозы, а также установить связи между ними.
Классическим представлением информации такого анализа является составление таблицы сильных сторон в деятельности организации, ее слабых сторон, потенциальных благоприятных возможностей и внешних угроз (табл. 12.8).
Таблица 12.8
| Среда | Положительное влияние | Отрицательное влияние |
|---|---|---|
| Внутренняя | Strengths — свойства организации, проекта, дающие преимущества перед другими в отрасли | Weaknesses — внутренние свойства, ослабляющие проект, организацию в целом и т.д. |
| Внешняя | Opportunities — внешние вероятные факторы, дающие дополнительные возможности по достижению цели | Threats — внешние вероятные факторы, которые могу т осложнить достижение цели |
На пересечении SW с ОТ проставляется экспертная оценка их взаимного влияния в баллах. Итоговая сумма баллов по строкам и столбцам показывает приоритетность учета того или иного фактора при формировании стратегии.
По итогам SWOT-анализа составляется матрица стратегических мероприятий:
- мероприятия, которые необходимо провести, чтобы использовать сильные стороны для увеличения возможностей организации;
- мероприятия, которые необходимо провести, преодолевая слабые стороны и используя представленные возможности;
- мероприятия, которые позволят использовать сильные стороны организации для устранения угроз;
- мероприятия, которые минимизируют слабые стороны организации для избежания угроз.
При использовании метода SWOT-анализа необходимо соблюдать несколько правил:
- максимально конкретизировать сферу проведения SWOT-анализа. При проведении анализа, охватывающего весь бизнес, его результаты скорее всего будут слишком обобщенными и бесполезными для практического применения;
- корректность при отнесении того или иного фактора к силам/ слабостям или возможностям/угрозам;
- использование разносторонней объективной информации.
SWOT-анализ — это лишь инструмент для структурирования имеющейся информации, он не даст ясных и четко сформулированных рекомендаций, конкретных ответов. Он лишь помогает наглядно представить основные факторы, а также оценить в первом приближении математическое ожидание тех или иных событий.
Простота SWOT-анализа обманчива, его результаты зависят от полноты и качества исходной информации. Ошибки, допущенные при формировании таблицы (включение лишних факторов или потеря важных, некорректная оценка весовых коэффициентов и взаимного влияния), трудно выявляются в процессе дальнейшего анализа и приводят к неверным выводам, а значит и ошибочным стратегическим решениям.
SWOT-анализ можно углубить при помощи метода PEST- анализа.
PEST-анализ — это метод анализа, позволяющий выявить политические (Policy), экономические (Economy), социальные (Society) и технологические (Technology) факторы внешней среды, которые могут повлиять на стратегию организации. Политика изучается потому, что она регулирует власть, которая в свою очередь определяет среду организации и получение ключевых ресурсов для ее деятельности. Основная причина изучения экономики — это создание картины распределения ресурсов на уровне государства, которая является важнейшим условием деятельности организации. Не менее важные потребительские предпочтения определяются с помощью социальной компоненты PEST-анализа. Целью исследования технологической компоненты является выявление и изучение тенденций в технологиях, которые изменяются в процессе научно-технического прогресса и часто являются причинами изменений и потерь рынка, а также появления новых продуктов.
Функционально-стоимостной анализ (ФСА) — метод технико-экономического исследования систем, направленный на оптимизацию соотношения между их потребительскими свойствами (способностью удовлетворять определенные потребности пользователя) и затратами на создание этих свойств. Иначе говоря, под функционально-стоимостным анализом понимается метод системного исследования функций отдельного изделия или определенного производственно-хозяйственного процесса, или же управленческой структуры, направленный на минимизацию затрат на стадиях проектирования, освоения производства, сбыта, промышленного и бытового потребления при определенном качестве, предельной полезности и долговечности.
Функционально-стоимостной анализ представляет собой эффективный способ выявления резервов сокращения затрат, который основывается на поиске более дешевых способов выполнения главных функций (путем организационных, технических, технологических и других изменений производства) при одновременном исключении лишних функций.
Конечной целью функционально стоимостного анализа является поиск наиболее экономичных с точки зрения потребителя и производителя вариантов того или иного практического решения.
Метод ФСА позволяет так реорганизовать деятельность, чтобы было достигнуто устойчивое сокращение стоимости, трудоемкости и времени. Для этого необходимо сделать следующее:
- сформировать ранжированный перечень функций по стоимости, трудоемкости или времени;
- выбрать функции с высокой стоимостью, трудоемкостью и затратами временем;
- устранить ненужные функции;
- сократить время, необходимое для выполнения функций;
- организовать совместное использование всех возможных функций;
- перераспределить ресурсы, высвободившиеся в результате усовершенствований.
Эти действия улучшают качество бизнес-процессов. Кроме того, повышение качества бизнес-процессов осуществляется за счет проведения сравнительной оценки и выбора рациональных (по стоимостному или временному критерию) технологий выполнения операций или процедур, являющихся элементами бизнес- процессов.
Функционально-стоимостной анализ основывается на следующем утверждении: каждый продукт, объект и т.д. производится, существует для того, чтобы удовлетворять определенные потребности (выполнять свои функции). При более детальном рассмотрении любого объекта можно увидеть, что он выполняет не одну, а всегда много функций. В процессе анализа их можно разделить на основные, вспомогательные и излишние (ненужные или вообще вредные). Однако в любом случае создание в предмете этих функций связано с определенными затратами средств. Отсюда очевидным становится тот факт, что если функции не нужны, то и затраты на их создание также лишние. Поэтому функционально-стоимостной анализ все затраты подразделяет на функционально-необходимые для выполнения объектом его функционального назначения и на излишние, порожденные неправильным выбором или несовершенством конструкторских решений.
Более того каждая функция, выполняемая объектом исследования, может реализовываться разными способами. Разные способы осуществления функции зависят от применяемых технологических и технических решений и соответственно, связаны с различными объемами затрат. Это позволяет выбрать такой способ осуществления определенной функции, который обеспечит и минимизацию затрат на ее создание. Таким образом, заменой существующего способа выполнения функции более дешевым достигается снижение себестоимости изделия.
С целью обеспечения наибольшей отдачи от использования метода ФСА необходимо соблюдать ряд принципов проведения аналитического исследования:
- принцип ранней диагностики, сущность которого состоит в том, что величина выявленных резервов зависит от того, на какой стадии жизненного цикла изделия проводится анализ: предпроизводственной, производственной, эксплуатации, утилизации. Как правило, излишние затраты в основном закладываются на этапе проектирования;
- принцип оптимальной детализации. Основной смысл проведения ФСА — выделение потребительских функций объекта исследования (продукта, процесса). Однако, если исследуемый объект достаточно сложен, то в результате его расчленения на отдельные функции их может образоваться слишком много. Такая узкая детализация затрудняет анализ и снижает его результативность. Поэтому целесообразно сначала разделить объект исследования на крупные части (отдельные узлы продукции, обособленные группы технологических операций, а затем для более глубокого изучения выделить в них более мелкие объекты);
- принцип последовательности предусматривает использование определенной логической схемы детализации — от общего к частному (объект — узел — функция). При этом результаты проведения анализа на каждом этапе зависят от полноты и качества исследования на предыдущих этапах;
- принцип выделения ведущего звена предполагает, что в любом объекте исследования (продукте, процессе) существует какая-то часть, которая требует больших затрат на обеспечение жизнеспособности этого объекта или сдерживает получение эффекта от его функционирования (использования). Поэтому в процессе исследования целесообразно основное внимание уделить именно этой части объекта анализа.
Таким образом, функционально-стоимостной анализ является важным средством повышения эффективности хозяйственной деятельности, укрепления конкурентоспособности продукции, ресурсосбережения.
Экономико-математические методы анализа
Применение экономико-математических методов расширяет возможности экономического анализа за счет сокращения времени проведения анализа, оценки влияния большего количества факторов на результаты хозяйственно-финансовой деятельности организации, повышения точности оценки их влияния, постановки и решения многомерных задач анализа, что особенно важно при проведении перспективного и стратегического анализа, роль которых в настоящее время возрастает.
В экономическом анализе используют математические модели, описывающие изучаемые явления, процессы с помощью уравнений, неравенств, функций и других математических средств. Экономико-математическая модель, адекватная действительности, позволяет выявить существенные стороны и взаимосвязи изучаемого объекта.
К экономико-математическим методам, достаточно широко используемым в экономическом анализе, можно отнести метод корреляционного и регрессионного анализа; эконометрические методы, теорию игр, теорию массового обслуживания, методы математического программирования, метод оптимизации товарных запасов (модель Уилсона) и др.
Корреляционный анализ основан на использовании вероятностных моделей, описывающих поведение исследуемых признаков в некоторой генеральной совокупности, из которой получены экспериментальные значения. Корреляция — статистическая взаимосвязь двух или нескольких случайных величии. При этом изменению значений одной или нескольких из этих величин сопутствует систематическое изменение значений другой или других величин. Математической мерой корреляции двух случайных величин служит линейный коэффициент корреляции (коэффициент корреляции Пирсона).
Этот метод анализа позволяет на основе использования достаточно большого массива экономической информации выявить и количественно измерить связи между экономическими явлениями, оценить тесноту этих связей и на данной основе выявить основные и второстепенные факторы, обусловившие то или иное экономическое явление, процесс.
В процессе корреляционного анализа решаются следующие задачи:
- установление формы и направления (положительное или отрицательное) связи между варьирующими признаками (линейная, нелинейная);
- измерение тесноты связи и проверка степени значимости полученных коэффициентов корреляции.
Корреляционный анализ чаще всего используют, чтобы установить взаимосвязи между экономическими показателями, находящимися не в функциональной, а в стохастической зависимости, т.е. когда изменение одного экономического показателя не вызывает определенное и неизбежное изменение другого.
Корреляционный анализ позволяет выявить тенденции изменения экономических явлений, построить математическую модель закономерностей изменения основного показателя (функции) в связи с изменением факторов (аргументов). Эта закономерность называется регрессией, а анализ ее свойств (поиск функциональных зависимостей у(х), графики которых являются центральными линиями корреляционного поля данных), называется регрессионным анализом корреляционной связи.
Регрессионный анализ — статистический метод исследования влияния одной или нескольких независимых переменных на зависимую переменную. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными.
Цели регрессионного анализа:
- определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными);
- предсказание значения зависимой переменной с помощью независимой (независимых);
- определение вклада отдельных независимых переменных в вариацию зависимой переменной.
Схема корреляционного анализа включает несколько этапов:
- сбор информации, расположение ее в определенной последовательности (по мере возрастания, убывания и другим признакам), группировка. Качественный анализ показателей, характер зависимости между которыми изучаются;
- логический анализ эмпирических данных об изменении результативного показателя и значений влияющего на него фактора, что позволяет сделать предположения относительно наличия и направления связи между признаком и фактором;
- графический анализ: данные располагают в виде точек на координатной плоскости. Координаты точек определяются соответствующими значениями пар переменных (х, у). Совокупность полученных точек называется корреляционным полем. Соединив последовательно на графике точки, строят ломаную линию, являющуюся эмпирической линией регрессии. По ее виду можно судить о форме взаимосвязи между экономическими явлениями и предположить тип теоретической линии регрессии;
- выбор уравнения связи;
- проверка соответствия предполагаемой функции фактическим данным путем расчетов коэффициента корреляции, остаточной дисперсии, построения доверительного интервала и т.д.
В том случае, если регрессионная модель устойчива во времени, ее можно использовать для проведения перспективного анализа и решения задач прогнозирования изменения результативного показателя.
Кластерный анализ применяется при изучении многомерных статистических совокупностей. Сущность его заключается в разбиении множества изучаемых объектов и признаков на однородные группы или кластеры. Кластерный анализ позволяет сгруппировать объекты исследования не по одному параметру, а по нескольким признакам. Он позволяет рассматривать достаточно большой объем информации, сжимать массивы социально-экономической информации, делать их компактными и наглядными. Важным вопросом при использовании этого метода является выбор критериев формирования групп объектов, так как при этом могут быть утеряны индивидуальные черты отдельных объектов за счет замены их характеристиками обобщенных значений параметра кластера.
В процессе проведения кластерного анализа необходимо на основании данных, содержащихся во множестве X, разбить на множество объектов G на m кластеров (подмножеств) Qm так, чтобы каждый объект G принадлежал только одному подмножеству разбиения и чтобы объекты, принадлежащие одному и тому же кластеру, были сходными, в то время как объекты, принадлежащие разным кластерам, были разнородными.
Теория игр — это теория математических моделей принятия оптимальных решений в условиях неопределенности или конфликта нескольких сторон, имеющих различные интересы. Теория игр позволяет исследовать конфликтные ситуации и на основе этого разрабатывать рекомендации по наиболее рациональному образу действий каждого из участников в ходе конфликтной ситуации. Формализуя конфликтные ситуации математически, их можно представить как игру двух, трех и более игроков, каждый из которых преследует цель максимизации своей выгоды, своего выигрыша за счет другого. Решения, получаемые с помощью теории игр, полезны при перспективном анализе возможных действий в условиях возможного противодействия конкурентов или неопределенности во внешней среде.
Игровую схему можно придать многим ситуациям в экономике. Здесь выигрышем могут быть эффективность использования дефицитных ресурсов, производственных фондов, величина прибыли, себестоимость и т.д. Теория игр может использоваться и для выбора оптимального решения, например, при создании запасов сырья, материалов, полуфабрикатов. В данном случае противоборствуют две тенденции: увеличения запасов, в том числе и страховых, гарантирующих бесперебойную работу производства, и сокращения запасов, обеспечивающих минимизацию затрат на их хранение.
Методы и рекомендации теории игр разрабатываются применительно к таким специфическим конфликтным ситуациям, которые обладают свойством многократной повторяемости. Если конфликтная ситуация реализуется однократно или ограниченное число раз, то рекомендации теории игр теряют смысл.
Для решения задач применяют алгебраические методы, основанные на системе линейных уравнений неравенств, итерационные методы, а также приведение задачи к системе дифференциальных уравнений.
Чтобы проанализировать конфликтную ситуацию по ее математической модели, ситуацию необходимо упростить, учтя лишь важнейшие факторы, существенно влияющие на ход конфликта.
Теория массового обслуживания изучает системы, предназначенные для обслуживания массового потока требований случайного характера (случайными могут быть как моменты появления требований, так и затраты времени на их обслуживание). Она исследует на основе теории вероятностей математические методы количественной оценки процессов массового обслуживания. Целью исследований является рациональный выбор структуры системы обслуживания и процесса обслуживания на основе изучения потоков требований на обслуживание, поступающих в систему и выходящие из нее, длительности ожидания и длины очередей. В теории массового обслуживания используются методы теории вероятностей и математической статистики. При этом зачастую требуются хронометражные наблюдения но обслуживанию потребителей. Целью анализа может быть определение вероятности отказа в предоставлении определенных услуг или обслуживании заявок.
Типичным примером объектов теории массового обслуживания могут служить автоматические телефонные станции, на которые случайным образом поступают «требования» вызовы абонентов, а «обслуживание» состоит в соединении абонентов с другими абонентами, поддержании связи во время разговора и т.д.
Использование методов теории массового обслуживания позволяет организовать обслуживание, обеспечивающее заданное его качество.
В системах массового обслуживания (СМО) обслуживаемый объект называют требованием. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, посадка самолета, покупка билета, покупка товаров в магазине и т.п.
Средства, обслуживающие требования, называются обслуживающими устройствами или каналами обслуживания. Например, к ним относятся каналы телефонной связи, кассовые аппараты в узлах расчетов магазинов, посадочные полосы, билетные кассиры и т.п.
В теории массового обслуживания рассматриваются такие случаи, когда поступление требований происходит через случайные промежутки времени, а продолжительность обслуживания требований не является постоянной, т.е. носит случайный характер. В силу этих причин одним из основных методов математического описания СМО является аппарат теории случайных процессов.
Основной задачей теории массового обслуживания является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания.
Так, одной из характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить за счет увеличения количества обслуживающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время бездействия обслуживающего устройства из-за отсутствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории массового обслуживания возникают задачи оптимизации: каким образом достичь определенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с простоем обслуживающих устройств.
Эконометрические методы строятся на синтезе трех областей знаний: экономики, математики и статистики. Основой эконометрии является экономическая модель, под которой понимается схематическое представление экономического явления или процесса с помощью научной абстракции, отражения их характерных черт. С помощью эконометрических методов следует оценивать различные величины и зависимости, используемые при построении имитационных моделей различных процессов, например, при анализе потоков платежей целесообразно использовать эконометрические модели инфляционных процессов, чтобы установить реальное соотношение авансовых и итоговых платежей.
Эконометрические модели могут использоваться для перспективного и стратегического анализа макроэкономических показателей. Это модели прогнозирования многомерного временного ряда, в которых оценивают как структуру модели, т.е. вид зависимости между значениями известных координат вектора в прежние моменты времени и их значениями в прогнозируемый момент, так и коэффициенты, входящие в эту зависимость.
Эконометрические методы — эффективный инструмент в работе менеджера, занимающегося конкретными проблемами, предназначенные для анализа статистических данных и построения эконометрических моделей конкретных экономических и технико-экономических явлений и процессов. Наибольшее распространение в современной экономике получил метод анализа экономики «затраты — выпуск». Это матричные (балансовые) модели, строящиеся по шахматной схеме и позволяющие в наиболее компактной форме представить взаимосвязь затрат и результатов производства.
Методы математического программирования — это основное средство решения задач оптимизации производственно-хозяйственной деятельности. По своей сути эти методы — средство плановых расчетов. Ценность их для экономического анализа заключается в том, что они позволяют оценивать напряженность плановых заданий, определять лимитирующие группы оборудования, виды сырья и материалов, получать оценки дефицитности производственных ресурсов и т.п.
Существуют следующие разделы математического программирования: линейное, параметрическое, нелинейное и динамическое программирование. Наиболее разработанным и широко применяемым разделом математического программирования является линейное программирование, целью которого является отыскание оптимума (max, min) заданной линейной функции при наличии ограничений в виде линейных уравнений или неравенств. Линейное программирование — математический прием, используемый для определения лучшей комбинации ресурсов и действий, необходимых для достижения оптимального результата.
Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи:
- рационального использования сырья и материалов; оптимизации производственной программы предприятий;
- оптимального размещения производства;
- составления оптимального плана перевозок, работы транспорта;
- многие другие, лежащие в сфере оптимального планирования.
Для большого количества практически интересных задач целевая функция выражается линейно — через характеристики плана, причем допустимые значения параметров подчинены линейным равенствам или неравенствам. Нахождение при данных условиях абсолютного экстремума целевой функции и носит название линейного программирования.
Прямая задача линейного программирования является математической формулировкой проблемы составления такого плана использования различных способов и факторов производства, который позволяет получить максимальное количество однородного продукта при имеющихся в наличии ресурсах.
Динамическое программирование — вычислительный метод для решения задач управления определенной структуры, когда задача с п переменными представляется как многошаговый процесс принятия решения. На каждом шаге определяется экстремум функции только от одной переменной. В этом случае исследование проходит три этапа:
- построение математической модели;
- решение управленческой задачи;
- анализ и обобщение полученных результатов.
Математические модели управления запасами позволяют найти оптимальный уровень запасов некоторого товара, минимизирующего суммарные затраты на покупку, оформление и доставку заказа, хранение. Модель Уилсона является простейшей моделью управления запасами и описывает ситуацию закупки продукции у поставщика, которая характеризуется следующими допущениями:
- интенсивность потребления является известной и постоянной величиной;
- заказ доставляется со склада, на котором хранится достаточный запас товара;
- время поставки заказа является известной и постоянной величиной;
- каждый заказ поставляется в виде одной партии;
- затраты на осуществление заказа не зависят от размера заказа;
- затраты на хранение запаса пропорциональны его размеру;
- отсутствие запаса (дефицит) является недопустимым.
Основной задачей формирования товарных запасов в торговле является обеспечение бесперебойного процесса реализации товаров, или достаточный запас сырья и материалов обеспечивает непрерывность производственного процесса.
В целом управление запасами включает в себя их анализ, планирование и оперативное перемещение. Эти задачи можно решать с помощью методов и моделей теории управления запасами. Целью этой теории является разработка методов и моделей выбора таких параметров управления, при которых достигается оптимум какого- либо критерия (max прибыли, min затрат и т.п.).
Формирование товарных запасов связано с расходованием денежных средств. Их величина зависит, прежде всего, от двух факторов: частоты завоза товаров и размера запаса, находящегося в организации. Таким образом, суммарные издержки по управлению запасами складываются из расходов по завозу товаров и расходов по хранению товаров в предприятии. Исходя из этого, основной задачей нормирования товарных запасов является определение такого планового объема запаса товаров, при котором эти совокупные расходы были бы минимальными, т.е. в качестве критерия оптимальности можно принять min издержек обращения.
Экономико-математическая модель задачи (детерминированная однономенклатурная модель Уилсона) имеет следующий вид:
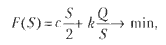
где F(S) — совокупные издержки по поставке и хранению товаров; Q — плановый объем оборота по реализации товаров; c — издержки хранения единицы товара в течение всего планового периода; k — затраты на завоз (закупку и доставку) одной партии товара; S — размер поставки.
Если использовать другие буквенные обозначения, то:
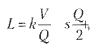
где L — совокупные издержки по поставке и хранению товаров; V — плановый объем оборота по реализации товаров; k — издержки хранения единицы товара в течение всего планового периода; s — затраты на завоз (закупку и доставку) одной партии товара; Q — размер поставки.
Циклы изменения уровня запаса в модели Уилсона графически представлены на рис. 12.1.
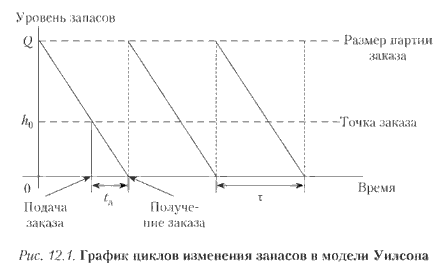
Максимальное количество продукции, которая находится в запасе, совпадает с размером заказа Q.
График затрат на управление запасами в модели Уилсона представлен на рис. 12.2.
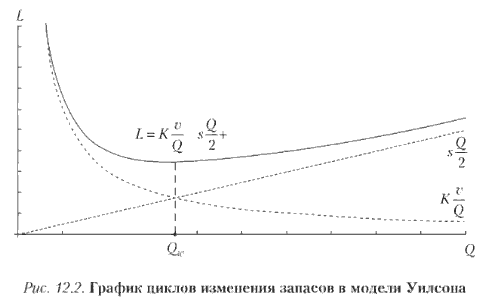
На практике возможны отклонения фактических значений параметров управления запасами от рассчитанных. В этом случае необходимо оценить влияние погрешностей при определении параметров на издержки управления товарными запасами, т.е. определить такие пределы отклонений параметров, которые не привели бы к существенному возрастанию издержек по управлению запасами. Следовательно, требуется определить относительное увеличение издержек по управлению запасами (b) при:
- отклонении фактического размера поставки от оптимального (а);
- отклонении рассчитанных издержек по доставке одной партии товара (либо издержек по хранению единицы товара, либо спроса) от фактических (g).
В экономическом анализе модель Уилсона применяется для изучения отклонений фактических издержек обращения от намеченных по плану, для перспективного анализа издержек производства и обращения продукции.
Графический метод экономического анализа
Для наглядного изображения экономико-математических моделей используют графики. Графики позволяют облегчить понимание экономико-математических моделей и отражаемых с их помощью хозяйственных (экономических) явлений, процессов.
Графиком называют наглядное изображение аналитических показателей при помощи геометрических линий и фигур (диаграмм). Графики обычно строят на основе данных статистических таблиц. Статистические таблицы высоко информативны и в определенной мере наглядны. Однако понимание их цифрового содержания требует времени, вдумчивой работы с цифрами и серьезного сравнительного анализа. Графическое изображение даже самых сложных статистических показателей делает их не только наглядными, по и доходчивыми и попятными с первого взгляда. График позволяет быстро уловить важнейшие тенденции и закономерности изучаемого явления. В отличие от лежащей в его основе таблицы, он дает предметную обобщающую картину состояния изучаемого явления, позволяет практически сходу заметить его особенности, содержащиеся в многочисленных количественных показателях, увидеть тенденции его изменения, выявить взаимосвязи с другими явлениями и процессами и даже предполагать его возможное развитие в будущем.
Графические модели не только позволяют описать связь между явлениями, но и дать количественную и качественную характеристику этой связи. В то же время возможность использования графиков ограничена известным человечеству числом пространственных измерений.
Важным и достаточно сложным вопросом построения графиков является разделение всей совокупности переменных на зависимые и независимые.
Под независимой переменной (причиной) понимается переменная, которая вызывает изменение другой — зависимой — переменной. В свою очередь, зависимая переменная — это переменная (результат), которая изменяется под влиянием изменения какой-то другой, независимой переменной.
Независимые переменные, как правило, на графиках показываются на оси X (горизонтальной), а зависимые переменные — на оси Y (вертикальной). В некоторых случаях для удобства восприятия графика независимые переменные могут показываться на оси Y, а зависимые — оси X (например, при изучении кривых спроса и предложения).
Графики, изображающие связь двух переменных, игнорируют влияние множества других факторов, от которых зависит результат, результирующий показатель. Поэтому при изображении связи между двумя переменными используется допущение «при прочих равных условиях».
Как и таблица, график имеет ряд признаков или элементов, знание которых позволяет правильно построить его вручную или машинным способом.
Основой любого графика являются:
- геометрические знаки (точки, линии, фигуры), с помощью которых изображаются статистические величины;
- пространственные ориентиры, определяющие размещение геометрических знаков на графике;
- поле, т.е. то место, где расположены геометрические знаки.
Пространственные ориентиры задаются в виде координатных сеток. В статистических графиках обычно применяется система прямоугольных координат в двумерном или трехмерном изображении. В картограммах средствами пространственной ориентации являются либо географические ориентиры (контуры дорог, рек, морей, лесов, населенных пунктов), либо административные или государственные границы. С пространственными ориентирами тесно связаны масштабные, которые дают графическим изображениям количественную определенность. Масштабные ориентиры определяются шкалами графика. В этом случае масштаб выполняет роль условной меры перевода количественных величин в графические. В статистических графиках, как правило, применяются прямолинейные масштабные шкалы. В связи с этим па осях абсцисс и ординат в условных масштабах откладываются соответствующие единицы измерения.
В графиках, построенных в форме круговых и секторных диаграмм, применяются кривоугольные шкалы. И прямоугольные, и кривоугольные шкалы могут быть равномерными и неравномерными.
Поле графика в зависимости от его целей и задач может быть чистым или заштрихованным. Последний метод часто применяется при подготовке графиков с помощью компьютерных программ, что позволяет более активно выделить те или иные графические образы. Размер поля зависит от назначения графика. Как и таблица, график должен иметь заголовки и словесные пояснения. Название графика чаще всего соответствует названию таблицы, на основе которой он построен. Он обязательно должен содержать наименования масштабных шкал: название отложенных на них единиц измерения (в абсолютных и относительных числах — в единицах, тысячах, коэффициентах, процентах и т.д.) и другие необходимые пояснения. В зависимости от целей графика, его количественной базы и применяемых геометрических знаков графики могут быть точечными (совокупность точек) и линейными.
Линейные и точечные графики имеют самое широкое распространение. Рассмотрим их использование в экономическом анализе на примере.
Пример 12.7
Пусть имеются данные эмпирических наблюдений о доходах семей какого-либо региона и доле их расходов на приобретение непродовольственных товаров в течение периода исследования (табл. 12.9).
Прежде всего, следует осмыслить данные табл. 12.9 и выяснить, имеет ли данная зависимость экономический смысл. Видимо, имеет, поскольку логично предположить, что семьи с более высоким уровнем доходов имеют возможность большую долю их тратить на покупку непродовольственных товаров. Более того, данная ситуация полностью описывается законом Энгеля, который гласит, что но мере роста доходов люди больше денег тратят на приобретение сначала более ценных в питательном отношении продуктов, а затем больше средств направляют на покупку непродовольственных товаров.
Таблица 12.9
| Доходы семьи (в среднем за месяц), руб. | Доля расходов на покупку непродовольственных товаров, % | Точки на графике |
|---|---|---|
| 5000 | 20 | А |
| 7500 | 25 | Б |
| 10000 | 30 | В |
| 12500 | 35 | Г |
| 15000 | 40 | Д |
| 17500 | 45 | Е |
Изобразим графически, как изменяется доля средств семей на покупку непродовольственных товаров но мере роста их доходов (рис. 12.3).
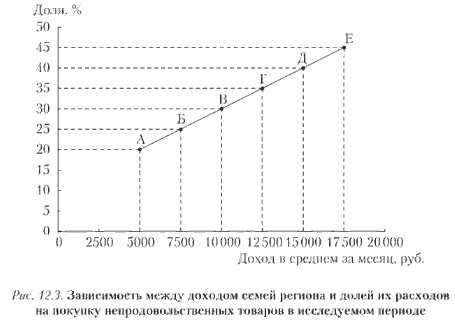
На рис. 12.3 видно, что полученная прямая линия является восходящей. Это говорит о наличии между рассматриваемыми переменными прямой связи, т.е. эти две переменные изменяются в одном и том же направлении. Когда между двумя рядами данных существует положительная, или прямая, зависимость, она всегда графически изображается в виде восходящей линии.
Связь между переменными может быть не только прямой, но и обратной. Например, обратная связь существует между размером дохода семьи и долей расходов на покупку продуктов питания. Если доход семьи снижается, то затраты на приобретение продуктов питания относительно возрастают, и наоборот, если доходы повышаются, то доля расходов на эти цели снижается (табл. 12.10).
Таблица 12.10
| Доходы семьи (в среднем за месяц), руб. | Доля расходов на покупку продовольственных товаров, % | Точки на графике |
|---|---|---|
| 5000 | 80 | А |
| 7500 | 75 | Б |
| 10000 | 70 | В |
| 12500 | 65 | Г |
| 15000 | 60 | Д |
| 17500 | 55 | Е |
Как видно из табл. 12.10, рассматриваемые переменные изменяются в противоположных направлениях, т.е. связь между ними обратная или, иначе говоря, отрицательная.
Построим на основе данных табл. 12.10 график (рис. 12.4), иллюстрирующий обратную (отрицательную) зависимость.
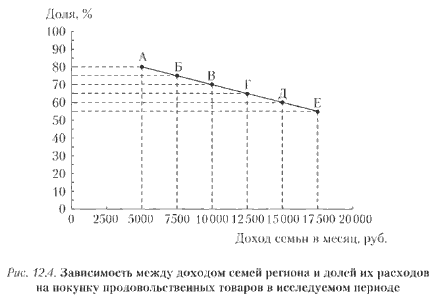
На рис. 12.4 видно, что полученная прямая линия является нисходящей. Это говорит о наличии между рассматриваемыми переменными обратной (отрицательной) связи, т.е. эти две переменные изменяются в одном и том же направлении. Когда между двумя рядами данных существует отрицательная, или обратная, зависимость, она всегда графически изображается в виде нисходящей линии.
Положение линии (прямой или кривой) на графике можно характеризовать по крутизне ее наклона и точке пересечения данной линии с осью ординат или, точнее, осью, на которой расположены значения зависимой переменной.
Наклон прямой линии между двумя точками определяется как отношение ее вертикального изменения (повышения или понижения) к горизонтальному изменению, обусловленное передвижением между точками.
| Наклон = | Вертикальное изменение | = | ΔY |
| Горизонтальное изменение | ΔX |
где ΔY — размер изменения зависимой переменной; ΔХ — размер изменения независимой переменной.
Определим наклон прямой линии, изображенной на рис. 12.3. Перемещаясь из точки Б в точку В, можно видеть, что повышение (или вертикальное изменение, характеризующее изменение) доли расходов на покупку непродовольственных товаров составляет +5% (30 - 25), а горизонтальное изменение, характеризующее изменение среднемесячного размера доходов семьи, составляет +2500 руб. (10000 - 7500). Отсюда:
Наклон = 1% / 500 руб.
Полученный наклон линии является положительным, поскольку размер среднемесячного дохода семьи и доля расходов на покупку непродовольственных товаров изменяются в одном и том же направлении, т.е. между ними существует прямая, или положительная, связь. На это указывает и знак +.
Наклон линии в +1/500 показывает, что с увеличением среднемесячного дохода семьи на каждые 500 руб. доля расходов на покупку непродовольственных товаров возрастает на 1%. Следовательно, если среднемесячный доход семьи возрастет на 4000 руб., то можно предположить и увеличение доли расходов, связанных с покупкой непродовольственных товаров, на 8%. Можно и иначе интерпретировать данный наклон, исходя из того, что переменные при прямой связи изменяются в одном и том же направлении: снижение среднемесячного дохода семьи на каждые 500 руб. влечет за собой и уменьшение доли расходов на покупку непродовольственных товаров на 1%. Это видно при движении из точки Д в точку Г (рис. 12.3). Наклон линии равен:
-5/-2500 = +1/500.
Рассмотрим наклон нисходящей прямой линии. Используем с этой целью рис. 12.4. Выделим на нем фрагмент, показывающий зависимость между изменением среднемесячного дохода семьи и доли расходов на покупку продуктов питания. Например, перемещаясь но прямой из точки Г в точку В, можно видеть, что снижение или вертикальное изменение, характеризующее изменение доли расходов на покупку продовольственных товаров, составляет -5% (65 - 70), а горизонтальное изменение, характеризующее изменение среднемесячного размера доходов семьи, составляет +2500 руб. (12500 - 10000). Отсюда:
Наклон = -5% / +2500 руб. = -1/500.
Полученный наклон линии является отрицательным, поскольку размер среднемесячного дохода семьи и доля расходов на покупку продовольственных товаров изменяются в противоположном направлении, т.е. между ними существует обратная, или отрицательная, связь. На это указывает и знак
Наклон линии в -1/500 показывает, что с уменьшением среднемесячного дохода семьи на каждые 500 руб. доля расходов на покупку продовольственных товаров возрастает на 1%. Следовательно, если среднемесячный доход семьи снизится, например, на 1500 руб., то можно предположить увеличение доли расходов, связанных с покупкой продовольственных товаров на 3%. Увеличение доходов семьи на каждые 500 руб. влечет за собой уменьшение доли расходов на покупку продовольственных товаров на 1%.
Учитывая то, что в некоторых случаях зависимые переменные показываются на оси абсцисс, для правильной экономической интерпретации положения прямой на графике следует уточнить ранее данное определение наклона прямой линии: наклон прямой линии рассчитывается как отношение изменения зависимой переменной на графике к изменению переменной независимой, обусловленное передвижением между точками на прямой, отражающей их взаимосвязь.
Таким образом, наклон линии показывает нам, как зависимая переменная реагирует на определенное изменение независимой переменной.
Наклон линии, в знаменателе которого стоит единичное значение независимой переменной, показывает меру реагирования зависимой переменной при изменении независимой переменной на одну единицу. Например, наклон линии, равный 1/500, можно изобразить (разделив числитель и знаменатель на 500) следующим образом: 0,002/1 или 0,002. Следовательно, при изменении среднемесячного дохода на 1 руб. доля расходов на покупку непродовольственных товаров изменится в том же направлении на 0,002%.
Рассмотрим точку пересечения прямой с осью ординат. Данная точка показывает значение зависимой переменной при отсутствии какого-либо влияния независимой переменной, так как на оси ординат (оси Y) значение независимой переменной равно нулю.
На рис. 12.3 эта точка находится на уровне 10% (чтобы это увидеть, нужно продлить прямую до пересечения с осью ординат). Данная величина означает, что если доходы семьи в текущем месяце равны по какой-то причине нулю, то она все равно 10% своих расходов направляет на приобретение непродовольственных товаров. Следует подчеркнуть, что рис. 12.3 (как и рис. 12.4) показывает зависимость доли расходов семьи на покупку непродовольственных (и, соответственно, продовольственных) товаров от величины доходов, полученных семьей в текущем месяце. Возможность приобретения непродовольственных товаров обусловлена, например, использованием денежных средств, полученных в долг (кредит), ранее накопленных денежных средств (сбережения). Ни займы, ни накопления отнести к доходам текущего месяца нельзя.
Поскольку в точке пересечения прямой (или кривой) с осью ординат влияние изучаемой переменной равно нулю, то данная точка показывает совокупное влияние всех остальных факторов на изучаемую зависимую переменную.
При движении по прямой но мере удаления от точки пересечения ее с осью ординат видно, что влияние этих факторов на зависимую переменную уменьшается абсолютно или относительно с одновременным возрастанием влияния изучаемой независимой переменной. Абсолютное уменьшение характерно для нисходящих прямых. Более того, двигаясь но нисходящей прямой сверху вниз, мы доходим до точки ее пересечения с осью абсцисс.
В этой точке, как видно из графика (рис. 12.5), значение зависимой переменной полностью определяется независимой переменной и влияние остальных факторов равно нулю.
На рис. 12.5 показана зависимость количества покупателей, приобретающих товары в магазине, от времени обслуживания одного покупателя.
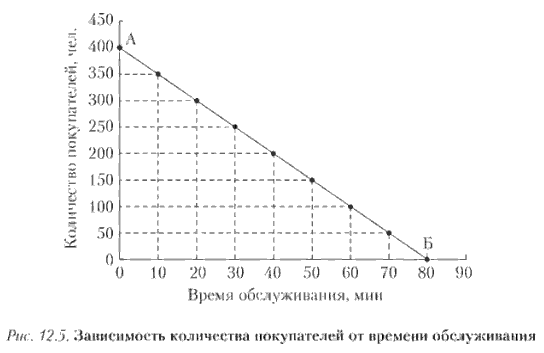
Из рис. 12.5 видно, что в точке А количество покупателей зависит только от других факторов в их совокупности, так как время обслуживания равно нулю. К этим факторам можно отнести численность продавцов, метод обслуживания, площадь торгового зала и др. По мере продвижения из точки А в точку Б видно, что роль этих факторов снижается, а роль фактора времени обслуживания возрастает, так как число покупателей постоянно уменьшается. В точке Б, лежащей на пересечении прямой с осью абсцисс, численность покупателей полностью определяется временем обслуживания, а влияние всех остальных факторов равно нулю. Из рис. 12.5 видно, что, если длительность обслуживания составляет 120 мин., покупатели полностью отказываются от совершения покупки в магазине, несмотря на все остальные привлекательные для них мотивы посещения этого магазина.
Соединив знания об экономической интерпретации наклона прямой линии и точки пересечения прямой с осью Y, можно описать рис. 12.3 в форме математического уравнения или, иначе говоря, написать экономико-математическую модель зависимости доли расходов на покупку непродовольственных товаров от среднемесячного дохода семьи.
В общем виде уравнение прямой выглядит следующим образом:
у = а + bх,
где у — зависимая переменная; а — точка пересечения прямой линии с осью Y; b — наклон линии; х — независимая переменная.
В рассматриваемом на рис. 12.3 примере у — это доля расходов на покупку непродовольственных товаров, выраженная в процентной форме. Параметр а равен 10%, параметр b равен +1/500, х — среднемесячный доход семьи. Подставим данные из рис. 12.3 в уравнение прямой и получим:
у = 10 + 0,002х
Из полученной экономико-математической модели (уравнения) видно, что при нулевом доходе доля расходов на покупку непродовольственных товаров составит 10% и далее по мере роста доходов семьи эта доля будет повышаться.
Экономико-математическую модель зависимости доли расходов на покупку продовольственных товаров от среднемесячного дохода семьи можно написать, используя рис. 12.4. Эта модель будет иметь следующий вид:
у = 90 — 0,002x.
Данная модель показывает, что при нулевом среднемесячном доходе доля расходов семей на покупку продовольственных товаров составит 90% и далее по мере роста доходов семьи эта доля будет снижаться в определенной пропорции.
Для иллюстрации табличной информации в экономическом анализе применяются также гистограммы, диаграммы и картограммы.
Гистограмма — это двумерный график распределения показателей. Они используются для демонстрации изменений данных за определенный период времени или для иллюстрации сравнения объектов. Гистограмму используют для изображения интервальных рядов. Для построения гистограммы по данным вариационного ряда с равными интервалами на оси абсцисс откладывают значения аргумента, а на оси ординат — значения частот или относительных частот. Далее строят прямоугольники, пирамиды, цилиндры, основаниями которых служат отрезки оси абсцисс, длины которых равны длинам интервалов, а высотами — отрезки, длины которых пропорциональны частотам или относительным частотам соответствующих интервалов.
Гистограммы могут быть плоскими, объемными, цилиндрическими, коническими, пирамидальными и др.
Диаграмма — это графическое представление данных, позволяющее быстро оценить соотношение нескольких величин. Она представляет собой геометрическое символьное изображение информации с применением различных приемов техники визуализации. Иногда для оформления диаграмм используется трехмерная визуализация, спроецированная на плоскость, что придает диаграмме отличительные черты или позволяет иметь общее представление об области, в которой она применяется. Например, финансовая диаграмма, связанная с денежными суммами, может представлять собой количество купюр в пачке или монет в стопке; диаграмма сравнения количества подвижного состава — различную длину изображенных поездов и т.д. Благодаря своей наглядности и удобству использования, диаграммы часто используются в аналитической работе. Диаграммы могут быть столбиковыми, полосовыми, квадратными, круговыми, поверхностными, пузырьковыми, лепестковыми и т.д.
Картограммы — это средства наглядного изображения фактических данных, которыми характеризуются отдельные районы, города, области и субъекты федерации. Примером может служить картограмма интенсивности продаж, где ее уровень в каждом регионе имеет свою окраску или штриховку. Картограммы нередко сочетаются с фигурными диаграммами, когда те или иные показатели на той или иной территории обозначаются фигурами: продажа продовольственных товаров, продажа парфюмерных товаров и т.д.
Графики, в которых используются рисунки отдельных предметов (товаров) или силуэтов (производственных, торговых предприятий) для обозначения соответствующей статистической картины, называют фигурными.
Компьютерная графика дает возможность строить более сложные и наглядные графики и диаграммы, позволяющие в максимально сжатом виде понятно и доходчиво показать реальное положение дел, которое сложнее понять при изучении таблиц или отдельных статистических показателей.
Вопросы и задания для самоконтроля
- По каким признакам классифицируются методы экономического анализа?
- Перечислите классические методы экономического анализа.
- Назовите неформализованные методы экономического анализа
- В каком случае применяют метод экспертной диагностики?
- Перечислите основные экономико-математические методы, используемые в экономическом анализе.
- Как используется в анализе метод абсолютных величин?
- Как используется в анализе метод относительных величин?
- С какой целью в процессе анализа используются средние величины?
- Дайте характеристику методу сравнения в экономическом анализе.
- С какими показателями сравниваются фактические результаты деятельности предприятия?
- В чем заключается метод группировки как способ анализа хозяйственной деятельности?
- В чем заключается сущность индексного метода анализа?
- Как рассчитать оборот (выручку) организации в сопоставимых ценах?
- В чем заключается сущность методов элиминирования?
- В чем заключается сущность метода разниц?
- В чем заключается сущность метода цепной подстановки?
- В чем заключается сущность балансового метода экономического анализа?
- Что понимается под независимой переменной?
- Раскройте понятие «функционально-стоимостной анализ (ФСА)», приведите примеры.
- Каковы цель и задачи ФСА?
- Раскройте значение маржинального анализа для обоснования управленческих решений.
- В чем сущность маржинального анализа?
- Какими способами можно определить величину условно-постоянных и переменных затрат?
- Охарактеризуйте сущность аналитического способа деления затрат на постоянные и переменные.
