Способы изучения корреляционных взаимосвязей

Корреляционная (стохастическая) связь – это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений. Различают парную и множественную корреляцию.

Парная корреляция – это связь между двумя показателями, один из которых является факторным, а другой результативным. Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем.

Для изучения стохастических соотношений используются следующие способы экономического анализа: сравнение параллельных и динамических рядов, аналитические группировки, графики. Однако они позволяют выявить только общий характер и направление связи. Для определения степени влияния каждого фактора на уровень результативного показателя применяются способы корреляционного, дисперсионного, компонентного, современного многомерного факторного анализа и т. д.

Наиболее широкое применение в экономических исследованиях нашли приемы корреляционного и регрессионного анализа, которые позволяют количественно выразить взаимосвязь между показателями.

Регрессионный анализ предназначен для выбора формы связей, типа модели, определения расчетных значений зависимой переменной (результирующего признака).

Применение корреляционного анализа позволяет решить следующие задачи:

1. Определить изменение результативного показателя под воздействием одного или нескольких факторов (в абсолютном измерении), т. е. выяснить, на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу.

2. Установить относительную степень зависимости результативного показателя от каждого фактора.

Необходимые условия применения корреляционного анализа:

1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов).
2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации.

При использовании способов парной корреляции связь между корреляционным фактором и результативным показателем характеризуется прежде всего коэффициентом корреляции, который может изменяться от нуля до единицы. Чем ближе он к единице, тем более тесная связь между анализируемыми показателями. Коэффициент корреляции с плюсом указывает на прямую связь, с минусом – на обратную:

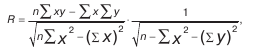
где р – число наблюдений; у – результативный показатель; x – факторный показатель.

Далее корреляционый анализ дополняется регрессионным анализом. Зависимость исследуемого показателя от одного фактора в простейшем виде можно представить формулой у = а + bx. Для определения параметров (а и b) этого уравнения используется метод наименьших квадратов, решается такая система уравнений:

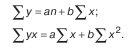
Размер влияния фактора на результат оценивается по параметру b (коэффициент регрессии), что показывает, на сколько единиц изменяется хозяйственный результат при изменении размера фактора на единицу.

При измерении тесноты связи при криволинейной зависимости используется универсальное корреляционное отношение:

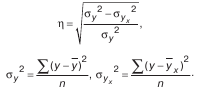
Множественный корреляционный анализ более сложен, он состоит из нескольких этапов:

1. Определение наиболее существенных факторов.
2. Сбор и оценка исходной информации.
3. Изучение характера и моделирование связи между факторами и результативным показателем (подбор математического уравнения, наиболее точно выражающего сущность связи).
4. Расчет показателей связи.
5. Статистическая оценка результатов корреляционного анализа.