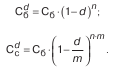Способы определения современной стоимости денег и наращенной суммы вложений
Одним из важнейших свойств денежных потоков является их распределенность во времени. Причины: инфляционное обесценивание денег, риск неполучения денег в будущем, возможность вложения денег и получения прибыли.
Количественной мерой изменения стоимости денег являются процентная и учетная ставки. С их помощью может быть определена будущая (наращенная) и настоящая стоимость денег (современная, текущая или приведенная). В первом случае используется операция наращения, во втором – дисконтирования или приведения будущей стоимости к ее современной величине (текущему моменту)
Формула процентной ставки:
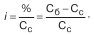
где % – абсолютная величина процента; С
с– современная стоимость С
б
– будущая стоимость денег.
Учетная ставка (ставка дисконта) определяется:
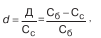
где Д – сумма дисконта. Первая формула отражает прирост текущей стоимости вторая – снижение будущей стоимости.
Наращенная сумма денег рассчитывается на основе начисления процентов. Существует два способа начисления процентов: декурсивный (начисление % в конце каждого временного интервала) и антисипативный (начисление % в начале каждого временного интервала)
Финансовая математика использует два вида процентов: простые и сложные проценты. При начислении простых процентов наращение первоначальной суммы происходит в арифметической прогрессии, а при начислении сложных процентов – в геометрической.
Начисление простых декурсивных и антисипативных процентов производится по формулам:
декурсивные проценты: С i б= С c ? (1+n?i)
антисипативные проценты:
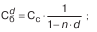
где n – продолжительность ссуды измеренная в годах
Наращение по антисипативному методу происходит более быстрыми темпами, чем при использовании процентной ставки. Недостаток: при n = 1/d знаменатель дроби обращается в нуль и выражение теряет смысл.
Особенностью простых процентов является то, что частота процессов наращения в течение года не влияет на результат. Если продолжительность ссуды не кратна году, определяется длительности ссуды в днях, вычисления ведутся по формулам:
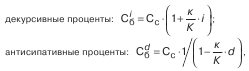
антисипативные проценты: С -О=С с
где к – продолжительность ссуды в днях; К – количество дней в году
Обратной задачей по отношению к начислению процентов является дисконтирование, в зависимости от того, какая именно ставка – простая процентная или простая учетная – применяется для дисконтирования, различают два его вида: математическое дисконтирование и банковский учет.
Дисконтирование по методу банковского учета использует простую учетную ставку:
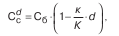
где к – срок, остающийся до погашения векселя, в днях. При математическом дисконтировании используется простая процентная ставка i
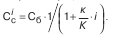
Основной областью применения простых процентной и учетной ставок являются краткосрочные финансовые операции, длительность которых менее года. Вычисления с простыми ставками не учитывают возможность реинвестирования начисленных процентов.
В отличие от них, сложные ставки процентов учитывают возможность реинвестирования процентов:
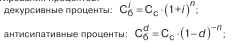
Важной особенностью сложных процентов является зависимость конечного результата от количества начислений в течение года:
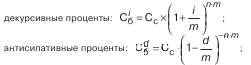
где m – количество начислений в год
Дисконтирование по сложным процентам также может выполняться двумя способами – математическое дисконтирование и банковский учет. Наиболее популярен банковский учет при однократном начислении процентов: